天津市和平区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-12 类型：期末考试

进入出卷网下载

一、单选题

1. 计算（-18）÷6的结果等于（）

A、-3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 多项式x²﹣3xy²﹣4的次数和常数项分别是（）

A、2和4 B、2和﹣4 C、3和4 D、3和﹣4

查看试题解析
3. 2020年5月，中科院沈阳自动化所主持研制的“海斗一号”万米海试成功，下潜深度超10900米，刷新我国潜水器最大下潜深度记录，将数据10900用科学记数法表示为（）

A、 $1.09 \times 10^{3}$ B、 $1.09 \times 10^{4}$ C、 $10.9 \times 10^{3}$ D、 $0.109 \times 10^{5}$

查看试题解析
4. 如图所示，由7个相同的小正方体组合成一个立体图形，从它上面看到的平面图形是（）

A、 B、 C、 D、

查看试题解析
5. 下列方程变形正确的是（）

A、由﹣5x＝2，得 $x = - \frac{5}{2}$ B、由 $\frac{1}{2} y = 1$ ，得y＝2 C、由3+x＝5，得x＝5+3 D、由3＝x﹣2，得x＝﹣2﹣3

查看试题解析
6. 如图，OA方向是北偏西40°方向，OB平分∠AOC，则∠BOC的度数为（）

A、50° B、55° C、60° D、65°

查看试题解析
7.
如图，从A到B有①，②，③三条路线，最短的路线是①，其理由是（　　）

A、因为它最直 B、两点确定一条直线 C、两点间的距离的概念 D、两点之间，线段最短

查看试题解析
8.
如图是一个正方体的展开图，把展开图折叠成正方体后，有“弘”字一面的相对面上的字是（）

A、传 B、统 C、文 D、化

查看试题解析
9. 如图所示，点 $C$ 是线段 $A B$ 的中点，点 $D$ 是线段 $C B$ 的中点，下列选项中错误的是（）

A、 $C D = A C - D B$ B、 $C D = A D - B C$ C、 $C D = \frac{1}{2} A B - D B$ D、 $C D = \frac{1}{3} A B$

查看试题解析
10. 如图：∠AOB：∠BOC：∠COD＝2：3：4，射线OM、ON，分别平分∠AOB与∠COD，又∠MON＝84°，则∠AOB为（）

A、28° B、30° C、32° D、38°

查看试题解析
11. 下列说法中，正确的有（）个．
①射线AB与射线BA是同一条射线；

②连接两点的线段叫做这两点的距离；

③把一个直角三角形以直角边为轴旋转一周得到的几何体是圆柱；

④等角的余角相等；

⑤因为AM＝MB，所以点M是AB的中点．

A、0个 B、1个 C、2个 D、3个

查看试题解析
12. 某中学学生军训，沿着与笔直的铁路并列的公路匀速前进，每小时走4.5千米．一列火车以每小时120千米的速度迎面开来，测得从火车头与队首学生相遇，到车尾与队末学生相遇，共经过12秒．如果队伍长150米，那么火车长（）

A、150 米 B、215米 C、265 米 D、310米

查看试题解析

二、填空题

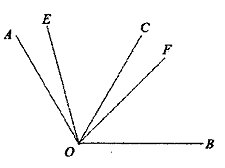
13. 31.46°＝度分秒．

查看试题解析
14. 已知a，b互为相反数，c，d互为倒数， x是数轴上到原点的距离为1的点表示的数，则 $x^{2020} - c d + \frac{a + b}{c d}$ 的值为.

查看试题解析
15. 当x＝1时，多项式ax²+bx+1的值为3，那么多项式2（3a﹣b）﹣（5a﹣3b）的值为．

查看试题解析
16. 一个角的补角比这个角的余角的4倍少60°，这个角的度数是（度）．

查看试题解析
17. 已知线段AB＝12cm，M是AB的中点，C是AB上一点，且AC＝5BC，则C、M两点之间的距离是cm．

查看试题解析
18. 我们定义：若两个角差的绝对值等于 $60^{\circ}$ ，则称这两个角互为“正角”，其中一个角是另一个角的“正角”，如： $∠ 1 = 110^{\circ}$ ， $∠ 2 = 50^{\circ}$ ， $| ∠ 1 - ∠ 2 | = 60^{\circ}$ ，则 $∠ 1$ 和 $∠ 2$ 互为“正角”.如图，已知 $∠ A O B = 120^{\circ}$ ，射线 $O C$ 平分 $∠ A O B$ ， $∠ E O F$ 在 $∠ A O B$ 的内部，若 $∠ E O F = 60^{\circ}$ ，则图中互为“正角”的共有对.

查看试题解析

三、解答题

19. 计算：

(1)、（﹣1）³﹣（ $\frac{1}{4} - \frac{2}{3}$ ）×（﹣2）²÷ $\frac{1}{(- 3^{2})}$ ﹣（﹣3）³；

(2)、﹣8÷ $\frac{4}{3} - [\frac{1}{4} - (1 - \frac{1}{2} \times \frac{1}{5})]$ ×20．

查看试题解析
20. 解下列方程：

(1)、 $\frac{2 x - 1}{3} - \frac{5 x + 2}{6} = \frac{1 - 2 x}{2}$ ﹣2；

(2)、 $\frac{3.1 + 0.2 x}{0.2} - \frac{0.2 + 0.03 x}{0.01} = \frac{3}{2}$ ．

查看试题解析
21. 已知A、B分别是关于x和y的多项式，一同学在计算多项式2A﹣B结果的时候，不小心把表示A的多项式弄脏了，现在只知道B＝2y²+3ay+2y﹣3，2A﹣B＝﹣4y²﹣ay﹣2y+1．

(1)、请根据仅有的信息试求出A表示的多项式；

(2)、若多项式A+2B中不含y项，求a的值．

查看试题解析
22. 如图，已知AB是直线，OD平分∠AOC，∠DOE＝90°．以射线OD为始边小于平角的所有角之和为330°．

(1)、求∠COD的度数；

(2)、反向延长射线OE得射线OF，先补全图形；再写出补全后图形中∠AOD的所有余角、∠COE的所有补角．

查看试题解析

23. 列方程解应用题：

一商场经销的A、B两种商品，A种商品每件进价40元，利润率为50%；B种商品每件进价50元，售价80元．

(1)、A种商品每件售价为元，每件B种商品利润率为%．

(2)、若该商场同时购进A、B两种商品共50件，恰好总进价为2100元，求购进A种商品多少件？

(3)、在“春节”期间，该商场只对A、B两种商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
少于等于450元	不优惠
超过450元，但不超过600元	按总售价打九折
超过600元	其中600元部分八折优惠，超过600元的部分打七折优惠

按上述优惠条件，若小华一次性购买A、B商品实际付款522元，求若没有优惠促销，小华在该商场购买同样商品要付多少元？

查看试题解析

24. 如图，直线l上有A，B两点，AB＝12cm，点O是线段AB上的一点，OA＝2OB．

(1)、则OA＝cm，OB＝cm；

(2)、若点C是线段AB上一点（点C不与点A、B重合），且满足AC＝CO+CB，求CO的长；

(3)、若动点P从点A出发，动点Q从点B同时出发，都向右运动，点P的速度为2cm/s．点Q的速度为1cm/s，设运动时间为t（s）（其中t≥0）．
①若把直线l看作以O为原点，向右为正方向的一条数轴，则t（s）后，P点所到的点表示的数为；此时，Q点所到的点表示的数为．（用含t的代数式表示）

②求当t为何值时，2OP﹣OQ＝4（cm）．

查看试题解析
25. 如图，点O是直线AB上的一点，∠COD＝80°，OE平分∠BOC．

(1)、如图1，若∠AOC＝40°，求∠DOE的度数．

(2)、在图1中若∠AOC＝α（其中20°＜α＜100°），请直接用含α的代数式表示∠DOE的度数，不用说明理由．

(3)、如图2，①请直接写出∠AOC和∠DOE的度数之间的关系，不用说明理由．
②在∠AOC的内部有一条射线OF，满足∠AOC﹣4∠AOF＝2∠BOE+∠AOF．试确定∠AOF与∠DOE的度数之间的关系，直接写出关系式即可，不用说明理由．

查看试题解析