河北省石家庄市辛集市2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-12 类型：期末考试

进入出卷网下载

一、单选题

1. 规定：（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作（）

A、+3 B、﹣3 C、﹣ $\frac{1}{3}$ D、+ $\frac{1}{3}$

查看试题解析
2. 下面的说法正确的是（）

A、正有理数和负有理数统称有理数 B、整数和分数统称有理数 C、正整数和负整数统称整数 D、有理数包括整数、自然数、零、负数和分数

查看试题解析
3. 已知|x﹣1|＝3，则x的值为（）

A、x＝4 B、x＝2或x＝﹣4 C、x＝4或x＝－2 D、x＝﹣3

查看试题解析
4. 在﹣5，﹣0.9，0，﹣0.01这四个数中，最大的负数是（）

A、﹣5 B、﹣0.9 C、0 D、﹣0.01

查看试题解析
5. 用四舍五入法按要求对 $21.67254$ 分别取近似值，其中正确的是（）

A、 $21.672$ （精确到百分位） B、 $21.673$ （精确到千分位） C、 $21.6$ （精确到 $0.1$ ） D、 $21.6726$ （精确到 $0.0001$ ）

查看试题解析
6. 舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约499.5亿千克，这个数用科学记数法应表示为（）

A、4.995×10¹¹ B、49.95×10¹⁰ C、0.4995×10¹¹ D、4.995×10¹⁰

查看试题解析
7. 轮船航行到C处测得小岛A的方向是北偏西20°，那么从A观察C处的方向为（）

A、南偏东20° B、西偏南70° C、南偏东70° D、西偏南20°

查看试题解析
8. 下列去括号的结果中，正确的是（）

A、 $- m + (- n^{2} + 3 m n) = - m + n^{2} + 3 m n$ B、 $4 m n + 4 n - (m^{2} - 2 m n) = 4 m n + 4 n - m^{2} + 2 m n$ C、 $- (a - c) + (b + d) = - a + b - c + d$ D、 $(- 3 b + 2 b^{2}) - (- 5 a) = 5 a - 3 b - 2 b^{2}$

查看试题解析
9. 如图，已知OC⊥OA，OD⊥OB．若∠AOB＝148°，则∠COD的度数为（）．

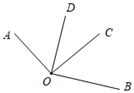A、58° B、32° C、48° D、52°

查看试题解析
10. 下列语句中，正确的个数是（）
①直线AB和直线BA是两条直线；②射线AB和射线BA是两条射线；③若∠1+∠2+∠3＝90°，则∠1、∠2、∠3互余；④一个角的余角比这个角的补角小；⑤一条射线就是一个周角；⑥两点之间，线段最短．

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 已知x＋y＋2（﹣x﹣y＋1）＝﹣4（y＋x＋1），则x＋y等于（）

A、﹣3 B、－2 C、5 D、2

查看试题解析
12. $x$ 是一个两位数， $y$ 是一个三位数，把 $x$ 放在 $y$ 的左边构成一个五位数，则这个五位数的表达式是（）

A、xy B、10x+y C、100x+1000y D、1000x+y

查看试题解析
13. 如图，数轴上A、B、C三点所表示的数分别是a、6、c．已知AB＝8，a＋c＝0，且c是关于x的方程（m－4）x＋16＝0的一个解，则m的值为（）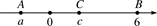

A、－4 B、2 C、4 D、6

查看试题解析
14. 由10个完全相同的小正方体搭成的物体如图所示．如果再添加若干个相同的小正方体之后，所得到的新物体从正面看和从左面看都跟原来的相同，那么这样的小正方体最多还可以添加（）个．

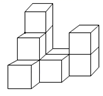A、3 B、4 C、5 D、6

查看试题解析
15. 书架上，第一层的数量是第二层书的数量的 $2$ 倍，从第一层抽 $8$ 本到第二层，这时第一层剩下的数量恰比第二层的一半多 $3$ 本，设第二层原有 $x$ 本，则可列方程（）

A、 $2 x = \frac{1}{2} x + 3$ B、 $2 x = \frac{1}{2} (x + 8) + 3$ C、 $2 x - 8 = \frac{1}{2} x + 3$ D、 $2 x - 8 = \frac{1}{2} (x + 8) + 3$

查看试题解析
16. 如图，是一个运算程序的示意图，若开始输入x的值为625，则第2020次输出的结果为（）

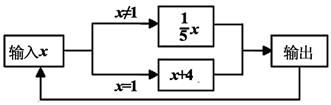A、1 B、5 C、25 D、625

查看试题解析

二、填空题

17. 单项式 $- \frac{2 a b}{3}$ 的系数是 $m$ ，多项式 $a^{2} b + 2 a b - 3$ 的次数是 $n$ ，则 $m + n =$ ．

查看试题解析
18. 某商店将彩电按成本价提高50%，然后在广告上写“大酬宾，八折优惠”，结果每台彩电仍获利270元，那么每台彩电成本价是．

查看试题解析
19. 我们知道，无限循环小数都可以转化为分数.例如：将 $0. \dot{6}$ 转化为分数时，可设 $x = 0. \dot{6}$ ，则 $10 x = 6. \dot{6}$ ， $10 x = 6 + 0. \dot{6}$ ， $10 x = 6 + x$ ，解得 $x = \frac{2}{3}$ ，即 $0. \dot{6} = \frac{2}{3}$ .仿此方法，将 $0. \dot{5}$ 化成分数是，将 $0. \dot{4} \dot{5}$ 化成分数是.

查看试题解析

三、解答题n

20. 计算：

(1)、3×（﹣4）＋（﹣6）﹣（﹣2）；

(2)、﹣3²×（﹣ $\frac{2}{9}$ ＋ $\frac{1}{3}$ ）﹣（﹣5）²÷（ $\frac{5}{3}$ ）² ．

查看试题解析
21. 先化简，再求值
6（x²y＋ $\frac{2}{3}$ xy²﹣ $\frac{1}{2}$ x）﹣ $\frac{3}{2}$ （4x²y＋2xy²＋8x），其中x＝ $\frac{1}{3}$ ，y＝1．

查看试题解析
22. 解方程

(1)、 $\frac{2 x + 1}{3} - \frac{x - 1}{6} = x + 2$ ．

(2)、 $x - 2 (2 x - 1) = 5$

查看试题解析
23. 如图，一个长方形运动场被分隔成A、B、A、B、C共5个区，A区是边长为a的正方形，C区是边长为b的正方形．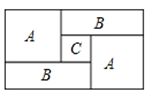

(1)、列式表示每个B区长方形场地的周长，并将式子化简；

(2)、列式表示整个长方形运动场的周长，并将式子化简；

(3)、如果a＝40，b＝10，求整个长方形运动场的面积

查看试题解析
24. 已知，如图，O为直线AB上一点，∠DOE＝90°．若∠AOC＝130°，OD平分∠AOC．

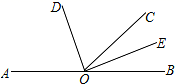(1)、求∠BOD的度数；

(2)、通过计算说明OE是否平分∠BOC．

查看试题解析
25. 已知线段AB，点C、点D在射线BA上，并且CD＝7，AC∶CB＝1∶2，BD∶AB＝1∶3．

(1)、工具画图：请根据题意画出符合条件的图形；

(2)、求出线段AB的长．

查看试题解析

26. 在“节能减排，做环保小卫士”活动中，小明对两种照明灯的使用情况进行了调查，得出如表所示的数据：

	功率	使用寿命	价格
普通白炽灯	100瓦（即0.1千瓦）	2000小时	3元/盏
优质节能灯	20瓦（即0.02千瓦）	4000小时	35元/盏

已知这两种灯的照明效果一样，小明家所在地的电价是每度0.5元．

（注：用电度数＝功率（千瓦）×时间（小时），费用＝灯的售价＋电费）

请解决以下问题：

(1)、在白炽灯的使用寿命内，设照明时间为x小时，请用含x的代数式分别表示用一盏白炽灯的费用y₁（元）和一盏节能灯的费用y₂（元）：

(2)、在白炽灯的使用寿命内，照明多少小时时，使用这两种灯的费用相等？

(3)、如果计划照明4000小时，购买哪一种灯更省钱？请你通过计算说明理由．

查看试题解析