河北省保定市雄县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-10-12 类型:期末考试
一、单选题
-
1. 下列运算结果为正数的是( )A、(﹣3)2 B、﹣3÷2 C、0×(﹣2017) D、2﹣32. 如图,将长方体的表面展开,得到的平面图形不可能是( )A、
 B、
B、 C、
C、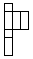 D、
D、 3. 下列语句中,错误的( )A、数字0也是单项式 B、单项式 的系数与次数都是1 C、 是二次单项式 D、 的系数是4. 某校食堂买了5袋白菜,以每袋20千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重后的记录分别为(单位:千克) , , , , ,请大家快速准确的算出5袋白菜的总质量是( )A、 千克 B、2千克 C、98千克 D、102千克5. 下列计算正确的是( )A、 B、 C、 D、6. 下列各式中,运算过程均运用了等式的性质变形,其中错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 计算 ( )A、 B、 C、 D、8. 如图,将甲、乙两个尺子拼在一起,两端重合.若甲尺经校订是直的,那么乙尺就一定不是直的,能正确解释这一现象的数学知识是( )
3. 下列语句中,错误的( )A、数字0也是单项式 B、单项式 的系数与次数都是1 C、 是二次单项式 D、 的系数是4. 某校食堂买了5袋白菜,以每袋20千克为标准,超过的千克数记为正数,不足的千克数记为负数,称重后的记录分别为(单位:千克) , , , , ,请大家快速准确的算出5袋白菜的总质量是( )A、 千克 B、2千克 C、98千克 D、102千克5. 下列计算正确的是( )A、 B、 C、 D、6. 下列各式中,运算过程均运用了等式的性质变形,其中错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 计算 ( )A、 B、 C、 D、8. 如图,将甲、乙两个尺子拼在一起,两端重合.若甲尺经校订是直的,那么乙尺就一定不是直的,能正确解释这一现象的数学知识是( )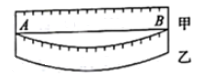 A、两点之间,线段最短 B、两点确定一条直线 C、两点之间,直线最短 D、直线可以向两边延长9. 王林同学在解关于x的方程3m+2x=4时,不小心将+2x看作了﹣2x,得到方程的解是x=1,那么原方程正确的解是( )A、x=2 B、x=﹣1 C、x= D、x=510. 已知矩形两边长为2cm与3cm,绕长边旋转一周所得几何体的体积为( )A、3πcm3 B、4πcm3 C、12πcm3 D、18πcm311. 下列说法正确的有( )
A、两点之间,线段最短 B、两点确定一条直线 C、两点之间,直线最短 D、直线可以向两边延长9. 王林同学在解关于x的方程3m+2x=4时,不小心将+2x看作了﹣2x,得到方程的解是x=1,那么原方程正确的解是( )A、x=2 B、x=﹣1 C、x= D、x=510. 已知矩形两边长为2cm与3cm,绕长边旋转一周所得几何体的体积为( )A、3πcm3 B、4πcm3 C、12πcm3 D、18πcm311. 下列说法正确的有( )①绝对值等于本身的数是正数;
②近似数4.60与4.6的精确度相同;
③连接两点的线段的长度就是两点间的距离;
④若 ,则点 就是线段 的中点.
A、1个 B、2个 C、3个 D、4个12. 定义 为二阶行列式,规定它的运算法则为 ,那么当 时,二阶行列式 的值为( )A、7 B、 C、1 D、13. 若 , 互为补角,且 ,则下列表示 的余角的式子中正确的是( )① ;② ;③ ;④ .
A、① B、② C、②③ D、②④14. 已知 , ,且 ,那么将 , , , 按照由大到小的顺序排列正确的是( )A、 B、 C、 D、15. 中国古代入民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有四人共车,一车空;二人共车,八人步,问人与车各几何?这道题的意思是:今有若干人乘车,每4人乘一车,最终剩余1辆车,若每2人共乘一车,最终剩余8个人无车可乘,问有多少人,多少辆车?如果我们设有x辆车,则可列方程( )A、 B、 C、 D、16. 已知有理数 、 的和 与差 在数轴上的大致位置如图所示,则以下判断① ② ③ 、 一定都是负数④ 是正数, 是负数.其中正确的判断( )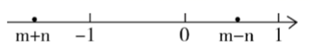 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
17. 地球离太阳约有一亿五千万千米,用科学记数法表示这个数是千米.18. 已知点O在直线AB上,且线段OA=4 cm,线段OB=6 cm,点E,F分别是OA,OB的中点,则线段EF=cm.19. 在如图所示的运算程序中,若开始输入的x值为96,我们发现第1次输出的结果为48,第⒉次输出的结果为24,…,第6次输出的结果为;第2021次输出的结果为 .

三、解答题
-
20.(1)、计算: ;(2)、化简: ;(3)、解方程: .21. 嘉淇准备完成题目;化简(
 )-( )时发现系数“
)-( )时发现系数“  ”印刷不清楚. (1)、她把“
”印刷不清楚. (1)、她把“ ”猜成3,请你化简 ,并求当 时的值. (2)、她妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
”猜成3,请你化简 ,并求当 时的值. (2)、她妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“ ”是几? (3)、若该题的化简结果中二次项系数是-1,通过计算说明原题中“
”是几? (3)、若该题的化简结果中二次项系数是-1,通过计算说明原题中“ ”是几? 22. 如图,已知平面内两点 .
”是几? 22. 如图,已知平面内两点 . (1)、请用尺规按下列要求作图,并保留作图痕迹;
(1)、请用尺规按下列要求作图,并保留作图痕迹;①连接 ;
②在线段 的延长线上取点 ,使 ;
③在线段 的延长线上取点 ,使 .
(2)、请求出线段 与线段 长度之间的数量关系.(3)、如果 ,则 的长度为 , 的长度为 , 的长度为 .23. 如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.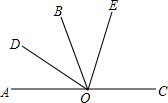 (1)、若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;(2)、若∠BOE= ∠EOC,∠DOE=72°,求∠EOC的度数.24. 下列是用火柴棒拼出的一列图形.
(1)、若OE是∠BOC的平分线,则有∠DOE=90°,试说明理由;(2)、若∠BOE= ∠EOC,∠DOE=72°,求∠EOC的度数.24. 下列是用火柴棒拼出的一列图形.
仔细观察,找出规律,解答下列各题:
(1)、第4个图形中共有根火柴,第6个图形中共有根火柴;(2)、第n个图形中共有根火柴(用含n的式子表示);(3)、请判断上组图形中前2021个图形火柴总数是2021的倍数吗?请说明理由.(参考: ,例如求解 )
25. 如图是某风景区的旅游线示意图,其中B、C、D为风景点,E为两条路的交叉点,图中数据为相应两点间的路程(单位:km),一学生从A处出发,以2km/h的速度步行游览,每个景点的逗留时间为0.5h.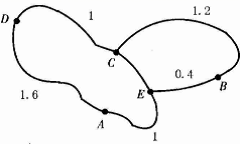 (1)、当他沿着路线A→D→C→E→A游览回到A处时,共用了3h,求CE的长;(2)、若此学生打算从A处出发后,步行速度与在景点逗留的时间不变,且在最短时间内看完三个景点回到A处,请你为他设计一个步行路线,并说明这样设计的理由(不考虑其他因素).26. 如图,点A,B,C在数轴上表示的数分别是-3,3和1,两动点P,Q同时出发,动点P从点A出发,以每秒6个单位的速度沿 往返运动,回到点A停止运动;动点Q从点C出发,以每秒1个单位的速度沿 向终点B匀速运动,设点P的运动时间为 .
(1)、当他沿着路线A→D→C→E→A游览回到A处时,共用了3h,求CE的长;(2)、若此学生打算从A处出发后,步行速度与在景点逗留的时间不变,且在最短时间内看完三个景点回到A处,请你为他设计一个步行路线,并说明这样设计的理由(不考虑其他因素).26. 如图,点A,B,C在数轴上表示的数分别是-3,3和1,两动点P,Q同时出发,动点P从点A出发,以每秒6个单位的速度沿 往返运动,回到点A停止运动;动点Q从点C出发,以每秒1个单位的速度沿 向终点B匀速运动,设点P的运动时间为 . (1)、当点Р到达点B时,求点Q所表示的数是;(2)、当 时,求线段PQ的长;(3)、当点P从点A向点B运动时,用含t的式子表示点P,Q之间的距离;(4)、在整个运动过程中,当P,Q两点到点C的距离相等时,直接写出t的值.
(1)、当点Р到达点B时,求点Q所表示的数是;(2)、当 时,求线段PQ的长;(3)、当点P从点A向点B运动时,用含t的式子表示点P,Q之间的距离;(4)、在整个运动过程中,当P,Q两点到点C的距离相等时,直接写出t的值.