河北省保定市清苑区南片区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-12 类型：期末考试

进入出卷网下载

一、单选题

1. 如果温度上升 $3 ℃$ ，记作 $+ 3 ℃$ ，那么温度下降 $2 ℃$ 记作（）

A、 $- 2 ℃$ B、 $+ 2 ℃$ C、 $+ 3 ℃$ D、 $- 3 ℃$

查看试题解析
2. 以下问题，不适合用全面调查的是（）

A、了解全班同学每周体育锻炼的时间 B、旅客上飞机前的安检 C、学校招聘教师，对应聘人员面试 D、了解全市中小学生每天的零花钱

查看试题解析
3. 下列四个生产生活现象，可以用基本事实“两点之间线段最短”来解释的是（　　）

A、用两颗钉子就可以把木条钉在墙上 B、植树时，只要定出两棵树的位置，就能确定同一行树所在的直线 C、从 $A$ 地到 $B$ 地架设电线，总是尽可能沿着线段 $A B$ 来架设 D、打靶的时候，眼睛要与枪上的准星、靶心在同一条直线上

查看试题解析
4. 如图所示，下列表示角的方法中，错误的是（）

A、 $∠ 1$ 与 $∠ A O B$ 表示同一个角 B、 $∠ A O C$ 也可用 $∠ O$ 表示 C、图中共有三个角，分别是 $∠ A O B ， ∠ A O C ， ∠ B O C$ D、 $∠ β$ 表示 $∠ B O C$

查看试题解析
5. 下列计算正确的是（）

A、 $- 2 - 1 = - 1$ B、 $- {(- 2)}^{3} = 8$ C、 $3 \div \frac{1}{3} \times 3 = 3$ D、 ${(- 2)}^{4} = 8$

查看试题解析
6. 人工智能AlphaGo因在人机大战中大胜韩国围棋手李世石九段而声名显赫．它具有自我对弈学习能力，决战前已做了20000000局的训练（等同于一个人近千年的训练量）．数字20000000用科学记数法表示为（）

A、 $0.2 \times 10^{7}$ B、 $2 \times 10^{7}$ C、 $0.2 \times 10^{8}$ D、 $2 \times 10^{8}$

查看试题解析
7. 如图，点C是线段AB的中点，点D是线段CB上任意一点，则下列表示线段关系的式子错误的是（）

A、AB=2AC B、AC+CD+DB=AB C、CD=AD- $\frac{1}{2}$ AB D、AD= $\frac{1}{2}$ （CD+AB）

查看试题解析
8.
若干桶方便面放在桌面上，如图是从正面、左面、上面看到的结果，则这一堆方便面共有（　　）

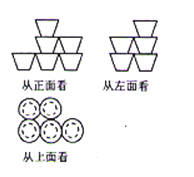A、7桶 B、8桶 C、9桶 D、10桶

查看试题解析
9.
如图，它需再添一个面，折叠后才能围成一个正方体，下图中的黑色小正方形分别由四位同学补画，其中正确的是（）

A、 B、 C、 D、

查看试题解析
10. 某天数学课上老师讲了整式的加减运算，小颖回到家后拿出自己的课堂笔记，认真地复习老师在课堂上所讲的内容，她突然发现一道题目： $(2 a^{2} + 3 a b - b^{2}) - (- 3 a^{2} + a b + 5 b^{2}) = 5 a^{2}$ $- 6 b^{2}$ ，空格的地方被墨水弄脏了，请问空格中的一项是（）

A、+2ab B、+3ab C、+4ab D、-ab

查看试题解析
11. 一轮船往返于A、B两港之间，逆水航行需3小时，顺水航行需2小时，水速是3千米/时，则轮船在静水中的速度是（）

A、18千米/时 B、15千米/时 C、12千米/时 D、20千米/时

查看试题解析
12. 若|m|＝5，|n|＝7，m+n＜0，则m﹣n的值是（）

A、﹣12或﹣2 B、﹣2或12 C、12或2 D、2或﹣12

查看试题解析
13. 为了解决老百姓看病难的问题，卫生部门决定大幅度降低药品价格，某种常用药品降价 $40%$ 后的价格为 $a$ 元，则降价前此药品的价格为（）

A、 $\frac{5}{2} a$ 元 B、 $\frac{5}{3} a$ 元 C、 $40 % \cdot a$ 元 D、 $60 % \cdot a$ 元

查看试题解析
14. 如图，在不完整的数轴上有A ， B两点，它们所表示的两个有理数互为相反数，则关于原点位置的描述正确的是（　　）

A、在点A的左侧 B、与线段AB 的中点重合 C、在点B的右侧 D、与点A或点B重合

查看试题解析
15. 如图，数轴上A、B两点对应的实数分别为a，b，则下列结论错误的是（）

A、a+b＞0 B、ab＜0 C、a﹣b＜0 D、|a|﹣|b|＞0

查看试题解析
16. 将一列有理数 $- 1 ， 2 ， - 3 ， 4 ， - 5 ， 6 ， \dots \dots$ ，如图所示有序排列，根据图中的排列规律可知：“峰1”中峰顶的位置（ $C$ 的位置）是有理数4，那么，“峰6”中 $C$ 的位置是有理数， $- 2013$ 应排在 $A 、 B 、 C 、 D 、 E$ 中的位置，其中两个填空依次为（）

A、 $- 28 ， C$ B、 $- 29 ， B$ C、 $- 30 ， D$ D、 $- 31 ， E$

查看试题解析

二、填空题

17. 每袋大米以50kg为标准，其中超过标准的千克数记为正数，不足的千克数记为负数，则图中第3袋大米的实际重量是 kg.

查看试题解析
18. 如图所示是一组有规律的图案，第l个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n（n是正整数）个图案中的基础图形个数为（用含n的式子表示）．

查看试题解析
19. 定义：若 $a + b = n$ ，则称a与b是关于整数n的“平衡数”比如3与 $- 4$ 是关于 $- 1$ 的“平衡数”，5与12是关于17的“平衡数”．请回答下列问题：

(1)、 $- 2$ 与 $- 3$ 是关于的“平衡数”．

(2)、现有 $a = 8 x^{2} - 6 k x + 14$ 与 $b = - 2 (4 x^{2} - 3 x + k)$ （k为常数），且a与b始终是整数n的“平衡数”，与x取值无关，则 $n =$ ．

查看试题解析
20. 数学课上，老师给出了如下问题：

(1)、以下是小刚的解答过程，请你将解答过程补充完整：
解：如图2，因为 $∠ A O B = 120 °$ ， $O C$ 平分 $∠ A O B$ ，

所以 $∠ B O C =$ $∠ A O B =$ $°$ （角平分线的定义）.

因为 $∠ C O D = 20 °$ ，

所以 $∠ B O D =$ $°$ .

(2)、小戴说：“我觉得这道题有两种情况，小刚考虑的是 $O D$ 在 $∠ B O C$ 内部的情况，事实上， $O D$ 还可能在 $∠ A O C$ 的内部”.根据小戴的想法，请你在图1中画出另一种情况对应的图形，并直接写出 $∠ B O D$ 的度数：.

查看试题解析

三、解答题

21. 计算：

(1)、 $(\frac{1}{6} - \frac{3}{4} + \frac{1}{12}) \times (- 48)$

(2)、 $2 - (- 4) + 8 \div (- 2) + (- 3)$

(3)、解方程： $5 - 2 x = 9 - 4 x$

(4)、解方程： $\frac{2 x - 1}{3} = 1 - \frac{5 x + 7}{6}$

查看试题解析
22. 某种杯子的高度是15cm，两个以及三个这样的杯子叠放时高度如图，

(1)、n个这样的杯子叠放在一起高度是 $($ 用含n的式子表示 $)$ ．

(2)、n个这样的杯子叠放在一起高度可以是35cm吗？为什么？

查看试题解析
23. 某校为了解“阳光体育”活动的开展情况，从全校2000名学生中，随机抽取部分学生进行问卷调查（每名学生只能填写一项自己喜欢的活动项目），并将调查结果绘制成如下两幅不完整的统计图．

根据以上信息，解答下列问题：

(1)、被调查的学生共有 ▲ 人，并补全条形统计图；

(2)、在扇形统计图中，m= ， n= ，表示区域C的圆心角为度；

(3)、全校学生中喜欢篮球的人数大约有．

查看试题解析
24. 先化简，再求值：
$2 (a^{2} b + a b^{2}) - 2 (a^{2} b - 1) - 2 a b^{2} - 2 a b$ ，其中 $a = - 2 ， b = 2$ ．

查看试题解析
25. 某商场经销的甲、乙两种商品，甲种商品每件售价60元，利润率为50%；乙种商品每件进价50元，售价80元．

(1)、甲种商品每件进价为元，每件乙种商品利润率为．

(2)、若该商场同时购进甲、乙两种商品共50件，恰好总进价为2100元，求购进甲种商品多少件？

查看试题解析
26. 已知如图，数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为 $t (t > 0)$ 秒．

(1)、数轴上点B表示的数是；当点P运动到 $A B$ 的中点时，它所表示的数是．

(2)、动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P，Q同时出发．求：
①当点P运动多少秒时，点P追上点Q？

②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

查看试题解析