河北省保定市安新县2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-12 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的相反数是（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 2018年10月24日港珠澳大桥全线通车，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门人工岛，止于珠海洪湾，它是世界上最长的跨海大析，被称为“新世界七大奇迹之一”，港珠澳大桥总长度5500000米，则数字5500000用科学记数法表示为（）

A、 $55 \times 10^{5}$ B、 $5.5 \times 10^{6}$ C、 $0.55 \times 10^{5}$ D、 $5.5 \times 10^{5}$

查看试题解析
3. 下面是小红所写的式子，其中，是一元一次方程的有（）
①5x﹣2；②3+5=﹣1+9；③5﹣ $\frac{1}{2}$ x=2x﹣8；④x=0；⑤x+2y=9．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列等式变形正确的是（）

A、如果 $S = \frac{1}{2} a b$ ，那么 $b = \frac{S}{2 a}$ B、如果 $\frac{1}{2} x = 6$ ，那么 $x = 3$ C、如果 $m x = m y$ ，那么 $x = y$ D、如果 $2 x - 3 = 2 y - 3$ ，那么 $x - y = 0$

查看试题解析
5. 下列对近似数的叙述错误的是（）

A、用四舍五入法对270.18（精确到个位）取近似值为270 B、用四舍五入法对0.518（精确到0.01）取近似值为0.52 C、由四舍五入法得到的近似数42.3万是精确到万位 D、由四舍五入法得到的近似数0.185是精确到千分位

查看试题解析
6. 下列说法中，正确的个数为（）
①单项式 $- \frac{2 π x^{2} y}{3}$ 的系数是 $- \frac{2}{3}$ ；②0是最小的有理数；③ $\frac{t}{2}$ 不是整式；④ $- 3 x^{3} y$ 的次数是4；⑤ $4 a b$ 与 $4 x y$ 是同类项；⑥ $\frac{1}{y}$ 是单项式；⑦连接两点的线段叫两点间的距离；⑧若点C是线段 $A B$ 的中点，则 $A C = B C$ ．

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 如果 $| a + 2 |$ 和 ${(b - 1)}^{2}$ 互为相反数，那么 ${(a + b)}^{2019}$ 的值是（）

A、 $- 2019$ B、2019 C、1 D、 $- 1$

查看试题解析
8. 已知关于x的方程3x+a＝0的解比关于x的方程5x﹣a＝0的解小1，则a的值为（）

A、﹣ $\frac{1}{8}$ B、 $\frac{1}{8}$ C、﹣ $\frac{15}{8}$ D、 $\frac{15}{8}$

查看试题解析
9. 若a与b互为相反数，c与d互为倒数，m的绝对值为2，则|m|﹣c×d+ $\frac{a + b}{m}$ 的值（）

A、1 B、﹣2 C、1或﹣3 D、 $\frac{3}{2}$ 或 $\frac{5}{2}$

查看试题解析
10. 定义 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ 为二阶行列式，规定它的运算法则为 $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ ，那么当 $x = 1$ 时，二阶行列式 $| \begin{matrix} x + 1 & x - 2 \\ 3 & - 5 \end{matrix} |$ 的值为（）

A、7 B、 $- 7$ C、1 D、 $- 1$

查看试题解析
11. 已知|a|=5，b³=﹣27，且a＞b，则a﹣b值为（）

A、2 B、﹣2或8 C、8 D、﹣2

查看试题解析
12. 如图，C、D是线段AB上的两个点，CD=3cm，M是AC的中点，N是DB的中点，AB=9.8cm，那么线段MN的长等于（）

A、5.4cm B、6.4cm C、6.8cm D、7cm

查看试题解析
13. 某小组有m人，计划做n个“中国结”，若每人做5个，则可比计划多做9个；若每人做4个，则将比计划少做15个，现有下列四个方程：① $5 m + 9 = 4 m - 15$ ；② $\frac{n - 9}{5} = \frac{n + 15}{4}$ ；③ $\frac{n + 9}{5} = \frac{n - 15}{4}$ ；④ $5 m - 9 = 4 m + 15$ ．其中正确的是（）

A、①② B、②④ C、②③ D、③④

查看试题解析

二、填空题

14. 宁城地区2015年冬季受降雪影响，气温变化异常，12月份某天早晨，气温为﹣13℃，中午上升了10℃，晚上又下降了8℃，则晚上气温为 ℃．

查看试题解析
15. 如图所示，在数轴上，点 $A$ 表示1，现将点 $A$ 沿轴做如下移动，第一次点 $A$ 向左移动3个单位长度到达点 $A_{1}$ ，第二次将点 $A_{1}$ 向右移动6个单位长度到达点 $A_{2}$ ，第三次将点 $A_{2}$ 向左移动9个单位长度到达点 $A_{3}$ ，按照这种移动规律移动下去，第 $n$ 次移动到点 $A_{n}$ ，如果点 $A_{n}$ 与原点的距离不小于20，那么 $n$ 的最小值是．

查看试题解析

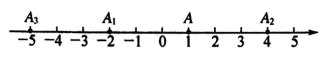
三、解答题

16. 计算

(1)、 $- 2 \frac{2}{5} - (+ 3 \frac{4}{11}) + (- \frac{3}{5}) - (- 1 \frac{7}{11})$

(2)、 $- 4^{2} \div {(- 2)}^{3} - \frac{4}{9} \times {(- \frac{3}{2})}^{2}$

查看试题解析
17.

(1)、 $\frac{2 x - 1}{2} - \frac{2 x + 5}{3} = \frac{6 x - 7}{6} - 1$ ．

(2)、3x+7=32-2x

查看试题解析
18. 如图，平面上有四个点A，B，C，D，请按要求画图：

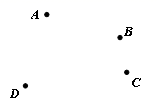
⑴作射线AB、DC交于点E；

⑵作线段AC，在线段AC上找到一点P，使其到B、D两个点的距离之和最短；

⑶作直线PE交线段AD于点M.

查看试题解析
19.

(1)、先化简，再求值： $3 x^{2} y - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y)] + 3 x y^{2}$ ，其中 $x = 3 ， y = - \frac{1}{3}$ ．

(2)、已知 $a + b = 7 ， a b = 10$ ，求代数式 $(5 a b + 4 a + 7 b) + (6 a - 3 a b) - (4 a b - 3 b)$ 的值．

查看试题解析
20. 如图， $∠ C O E$ 与 $∠ E O D$ 互余， $O E$ 平分 $∠ A O D$ ，已知 $∠ A O B = 140 °$ ．

(1)、若 $∠ C O E = 40 °$ ，则 $∠ D O E =$ ， $∠ B O D =$ ．

(2)、设 $∠ C O E = α$ ， $∠ B O D = β$ ，请探究 $α$ 与 $β$ 之间的数量关系．

查看试题解析
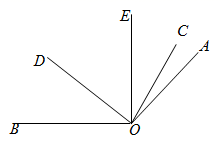21. 某市自来水公司为限制单位用水，每月只给某单位计划内用水300吨，计划内用水每吨收费3.4元，超过计划的部分每吨按4.6元收费．

(1)、当该单位每月用水250吨时，需付款元；当该单位每月用水350吨时，需付款元；

(2)、若某单位4月份缴纳水费1480元，则该单位用水多少吨？

(3)、若某单位5、6月份共用水700吨（6月份用水量超过5月份），共交水费2560元，则该单位5月份用水吨．

查看试题解析
22. 若A、B、C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是（A，B）的好点．

(1)、如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是（A，B）的好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D（A，B）的好点，但点D（B，A）的好点．（请在横线上填是或不是）

(2)、如图2，M、N为数轴上两点，点M所表示的数为4，点N所表示的数为-2．数所表示的点是（M，N）的好点；

(3)、如图3，A、B为数轴上两点，点A所表示的数为-20，点B所表示的数为40．现有一只电子蚂蚁P从点B出发，以4个单位每秒的速度向左运动，到达点A停止．当经过秒时，P、A和B中恰有一个点为其余两点的好点？

查看试题解析