北京市东城区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-10-12 类型：期末考试

进入出卷网下载

一、单选题

1. 四个有理数 $- \frac{2}{3} ， - 1 ， 0 ， 1$ ，其中最小的是（）

A、 $- \frac{2}{3}$ B、 $- 1$ C、0 D、1

查看试题解析
2. 2020年国庆中秋黄金周非比寻常，八天长假期间，全国共接待国内游客约 $637000000$ 人次，按可比口径同比恢复 $79 %$ .将数据 $637000000$ 用科学记数法表示应为（）

A、 $6.37 \times 10^{8}$ B、 $6.37 \times 10^{9}$ C、 $63.7 \times 10^{7}$ D、 $0.637 \times 10^{9}$

查看试题解析
3. 将如图所示的直角梯形绕直线l旋转一周，得到的立体图形是（　　）

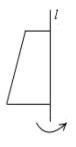A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $5 a b^{2} - 5 a^{2} b = 0$ C、 $7 a + a = 7 a^{2}$ D、 $- a b + 3 b a = 2 a b$

查看试题解析
5. 若有理数 $a$ ， $b$ 在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $a > - 2$ B、 $a > - b$ C、 $a b < 0$ D、 $| a | < | b |$

查看试题解析
6. 按照如图所示的操作步骤进行计算，若输入的值为 $- 3$ ，则输出的值为（）

A、 $0$ B、 $4$ C、 $55$ D、 $60$

查看试题解析
7. 一副三角板按如图所示的方式摆放，且 $∠ 1$ 的度数是 $∠ 2$ 度数的三倍，则 $∠ 2$ 的度数为（）

A、 $15 °$ B、 $22.5 °$ C、 $30 °$ D、 $67.5 °$

查看试题解析
8. 已知点 $C$ 在线段 $A B$ 上，点D在线段 $A B$ 的延长线上，若 $A C = 5$ ， $B C = 3$ ， $B D ＝ \frac{1}{4} A B$ ，则 $C D$ 的长为（）

A、 $2$ B、 $5$ C、 $7$ D、 $5$ 或 $1$

查看试题解析
9. 已知 $x$ ， $y$ 满足方程组 ${\begin{array}{l} x + 5 y = 12 \\ 3 x - y = 4 \end{array}$ ，则 $x + y$ 的值为（）

A、 $- 4$ B、 $- 2$ C、 $4$ D、 $2$

查看试题解析
10. 南锣鼓巷是全国首个引导游客开展垃圾分类的特色商业街区．据统计，街区每天产生垃圾中量最大的就是餐馆产生的厨余垃圾，而垃圾总量是厨余垃圾的 $2$ 倍少 $6$ 吨．“十一”期间南锣鼓巷主街商户劝导食客开展“光盘行动”后，每天能减少 $6$ 吨厨余垃圾，现在的厨余垃圾相当于“光盘行动”前垃圾总重量的三分之一．设“光盘行动”前每天产生厨余垃圾 $x$ 吨，可列方程为（）

A、 $x - 6 = \frac{1}{3} (2 x - 6)$ B、 $x + 6 = \frac{1}{3} (2 x - 6)$ C、 $\frac{1}{3} (x - 6) = 2 x - 6$ D、 $\frac{1}{3} (x + 6) = 2 x - 6$

查看试题解析

二、填空题

11. 单项式﹣2xy²的系数是，次数是．

查看试题解析
12. 已知x＝2是方程2x﹣5＝x+m的解，则m的值是．

查看试题解析
13. 已知 $m - 3 n = 2$ ，则 $5 - 2 m + 6 n$ 的值为．

查看试题解析
14. 等式 $a x - 3 x = 3$ 中，若 $x$ 是正整数，则整数 $a$ 的取值是．

查看试题解析
15. 若一个角的余角是它的补角的 $\frac{1}{6}$ ，则这个角的度数为．

查看试题解析
16. 如图所示，甲、乙三艘轮船从港口 $O$ 出发，当分别行驶到 $A$ ， $B$ 处时，经测量，甲船位于港口的北偏东 $44 °$ 方向，乙船位于港口的北偏西 $46 °$ 方向，则 $∠ A O B$ 等于度．

查看试题解析
17. 已知 $A$ ， $B$ ， $C$ 为直线l上的三点，如果线段 $A B ＝ 3 c m$ ， $B C ＝ 6 c m$ ，那么 $A$ ， $C$ 两点间的距离为．

查看试题解析
18. 如图，在 $∠ A O B$ 的内部有 $3$ 条射线 $O C$ ， $O D$ ， $O E$ ，若 $∠ A O C = 50 °$ ， $∠ B O E = \frac{1}{n} ∠ B O C$ ， $∠ B O D = \frac{1}{n} ∠ A O B$ ，则 $∠ D O E =$ $°$ （用含 $n$ 的代数式表示）．

查看试题解析

三、解答题

19. 计算题：

(1)、 $| - 12 | - (- 18) + (- 7) + 6$ ；

(2)、 $- 1^{2} - (- 32) \times (\frac{3}{4} - 2 \frac{1}{2} + 1 \frac{5}{8})$ ；

(3)、 $\frac{1}{6} \times [1 - {(- 3)}^{2}] \div (- \frac{1}{3})$ ．

查看试题解析
20. 解方程或方程组：

(1)、 $7 - 2 x = 3 - 4 (x - 2)$ ；

(2)、 $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$ ；（按要求解方程并在括号里注明此步依据）
解：去分母，得    ▲    ．（）

去括号，得    ▲    （）

移项，得    ▲    （）

合并同类项，得    ▲    ．

系数化为“ $1$ ”，得    ▲    ．

(3)、 ${\begin{array}{l} 5 x + 2 y = 25 \\ 3 x + 4 y = 15 \end{array}$

查看试题解析
21. 已知 $A = 2 a^{2} + 3 a b - 2 a - 1$ ， $B = - a^{2} + a b + 2$ ．

(1)、化简： $4 A - (3 A - 2 B)$ ；

(2)、若（1）中式子的值与 $a$ 的取值无关，求 $b$ 的值．

查看试题解析
22. 如图，平面内有四个点A，B，C，D．根据下列语句画图：

①画直线BC；

②画射线AD交直线 $B C$ 于点E；

③连接BD，用圆规在线段BD的延长线上截取DF=BD；

④在图中确定点O，使点O到点A，B，C，D的距离之和最小.

（友情提醒：截取用圆规，并保留痕迹；画完图要下结论）

查看试题解析
23. 如图为北京市地铁 $1$ 号线地图的一部分，某天，小王参加志愿者服务活动，从西单站出发，到从 $A$ 站出站时，本次志愿者服务活动结束，如果规定向东为正，向西为负，当天的乘车站数按先后顺序依次记录如下（单位：站）： $+ 4$ ， $- 3$ ， $+ 6$ ， $- 8$ ， $+ 9$ ， $- 2$ ， $- 7$ ， $+ 1$ ．

(1)、请通过计算说明 $A$ 站是哪一站？

(2)、若相邻两站之间的平均距离为 $1.2$ 千米，求这次小王志愿服务期间乘坐地铁行进的总路程约是多少千米？

查看试题解析
24. 补全解题过程：如图，已知线段 $A B = 6$ ，延长 $A B$ 至 $C$ ，使 $B C = 2 A B$ ，点 $P$ 、 $Q$ 分别是线段 $A C$ 和 $A B$ 的中点，求 $P Q$ 的长.

解： $∵ B C = 2 A B$ ， $A B = 6$

$∴ B C = 2 \times 6 = 12$

$∴ A C =$     ▲    $+$     ▲    $= 6 + 12 = 18$

$∵$ 点 $P$ 、 $Q$ 分别是线段 $A C$ 和 $A B$ 的中点

$∴ A P = \frac{1}{2}$     ▲    $= \frac{1}{2} \times 18 = 9$

$A Q = \frac{1}{2}$     ▲    $= \frac{1}{2} \times 6 = 3$

$∴ P Q =$     ▲    -    ▲    $= 9 - 3 = 6$

查看试题解析
25. 如图，点 $O$ 为直线 $A B$ 上一点， $∠ B O C ＝ 36 °$ ， $O D$ 平分 $∠ A O C$ ， $∠ D O E = 90 °$ ，求 $∠ A O E$ 的度数．

查看试题解析
26. 我们规定：若关于 $x$ 的一元一次方程 $a + x = b (a \neq 0)$ 的解为 $x = \frac{b}{a}$ ，则称该方程为“商解方程”．例如： $2 + x = 4$ 的解为 $x = 2$ 且 $2 = \frac{4}{2}$ ，则方程 $2 + x = 4$ 是“商解方程”．请回答下列问题：

(1)、判断 $3 + x = 4.5$ 是不是“商解方程”；

(2)、若关于 $x$ 的一元一次方程是 $4 + x = 2 (m - 3)$ “商解方程”，求 $m$ 的值．

查看试题解析
27. 自动驾驶汽车是一种通过电脑系统实现无人驾驶的智能汽车．某出租车公司拟在今明两年共投资 $9000$ 万元改造260辆无人驾驶出租车投放市场．今年每辆无人驾驶出租车的改造费用是5 $0$ 万元，预计明年每辆无人驾驶出租车的改造费用可下降50%．求明年改造的无人驾驶出租车是多少辆．

查看试题解析
28. 某校七年级准备观看电影《我和我的祖国》，由各班班长负责买票，每班人数都多于 $40$ 人，票价每张 $30$ 元，一班班长问售票员买团体票是否可以优惠，售票员说： $40$ 人以上的团体票有两种优惠方案可选择：
方案一：全体人员可打 $8$ 折；方案二：若打 $9$ 折，有 $5$ 人可以免票．

(1)、若二班有 $41$ 名学生，则他该选择哪个方案？

(2)、一班班长思考一会儿说，我们班无论选择哪种方案要付的钱是一样的，你知道一班有多少人吗？

查看试题解析