北京市昌平区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-10-12 类型:期末考试
一、单选题
-
1. 如果支出50元记作-50元,那么收入100元记作( )A、+100元 B、-100元 C、+50元 D、-50元2. -6的绝对值是( )A、-6 B、6 C、- D、3. 下列等式中成立的是( )A、a﹣(b+c)=a﹣b+c B、a+(b+c)=a﹣b+c C、a+b﹣c=a+(b﹣c) D、a﹣b+c=a﹣(b+c)4. 自2020年5月1日《北京市生活垃圾管理条例》实施以来,本市居民家庭厨余垃圾分出量大幅提升,分出量从《条例》实施前的每日309吨,增长至10月份的每日3946吨,增长了约12倍.预计2021年1月(31天)厨余垃圾的日均分出量约为5000吨,那么该月可分出厨余垃圾的总量用科学记数法表示为( )A、 B、 C、 D、5. 下列各数中,是负整数的是( )A、 B、 C、 D、6. 如果 与 是同类项,那么( )A、 , B、 , C、 , D、 ,7. 用若干根等长的小木棍搭建等边三角形(三边相等的三角形),搭建1个等边三角形最少需要3根小木棍,搭建2个等边三角形最少需要5根小木棍,搭建4个等边三角形最少需要小木棍的根数是( )A、12 B、10 C、9 D、6
二、填空题
-
8. ﹣ 的倒数是 .9. 比较大小:-7-5.10. 用列代数式表示“a的3倍与b的和”为 .11. 如果关于x的方程 的解是 ,那么a的值是 .12. 如图,已知 于点O, ,那么 ′.
 13. 已知 ,则 的值为 .14. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能符合题意解释这一现象的数学知识是 .
13. 已知 ,则 的值为 .14. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能符合题意解释这一现象的数学知识是 .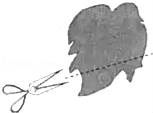 15. (问题)将 化为分数形式.
15. (问题)将 化为分数形式.(探求)步骤①设 .
步骤② .
步骤③ ,则 .
步骤④ ,解得: .
(回答)
(1)、 化为分数形式得;(2)、 化为分数形式得 .三、解答题
-
16. 计算: .17. 计算: .18. 计算: .19. 解方程: .20. 解方程: .21. 在学习了整式的加减后,老师在课堂上布置了一道练习:
已知:代数式 .
当(1) ;(2) ;(3) 时,从中选择a的一个取值代入代数式求值,看谁算的快.
小丹立马举手说:“我选 ,结果是2021,因为 时,含a的每一项都是0,0和任何有理数相加仍得这个有理数”;
小良随后举手说:“代入1或 的结果也是2021”;
小涛思考后举手说:“代入任何一个数的结果都是2021”.
你验证小涛的说法是正确的.
22. 补全解题过程.已知:如图, , , 平分 .
求 的度数.

解:∵ , ,
∴ ▲ = ▲ °.
∵ 平分 ,
∴ ▲ .( ▲ )
∴ .
∴ ▲ = ▲ °.
23. 如图,已知一条笔直的公路l的附近有A,B,C三个村庄.
⑴画出村庄A,C间距离最短的路线;
⑵加油站D在村庄B,C所在直线与公路l的交点处,画出加油站D的位置;
⑶画出村庄C到公路l的最短路线 ,作图依据是 ▲ , 测量 ▲ (精确到 );如果示意图与实际距离的比例尺是1∶200000,通过你的测量和计算,在实际中村庄C到公路l的最短路线为 ▲ .
24. 列方程解应用题.我国古代数学名著《算法统宗》中有这样一个问题:隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.问:人数多少?银子几何?意思是:有若干客人分银若干两,如果每人分7两,还多4两;如果每人分9两,还差8两(题中斤、两为旧制,1斤 两).问:有多少位客人?多少两银子?
25. 已知直线l上有A,B,C,D四点, , ,点D是线段 的中点,根据题意画出图形,并求线段 的长.26. 数学课上李老师说:咱们一起来玩儿一个找原点的游戏吧!(1)、如图1,在数轴上标有A,B两点,已知A,B两点所表示的数互为相反数.①如果点A所表示的数是 ,那么点B所表示的数是 ▲ ;
②在图1中标出原点O的位置;
 (2)、图2是小慧所画的数轴,数轴上标出的点中任意相邻两点间的距离都相等.
(2)、图2是小慧所画的数轴,数轴上标出的点中任意相邻两点间的距离都相等.根据小慧提供的信息,标出隐藏的原点O的位置,写出此时点C所表示的数是 ▲ ;
 (3)、如图3,数轴上标出若干个点,其中点A,B,C,D所表示的数分别为a,b,c,d.
(3)、如图3,数轴上标出若干个点,其中点A,B,C,D所表示的数分别为a,b,c,d.①用a,c表示线段 的长为 ▲ ;
②如果数轴上标出的若干个点中每相邻两点相距1个单位(如 ),且 .判断此时数轴上的原点是A,B,C,D中的哪一点,并说明理由.
 27. 规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方.
27. 规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方.例如 ,记作 ,读作“2的圈3次方”;
再例如 ,记作 ,读作“ 的圈4次方”;一般地,把 ( ,n为大于等于2的整数)记作 ,读作“a的圈n次方”.
(1)、①直接写出计算结果: , ;②关于除方,下列说法错误的是;
A.任何非零数的圈2次方都等于1;
B.对于任何大于等于2的整数c, ;
C. ;
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数;
(2)、我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?除方 乘方幂的形式
①仿照上面的算式,将下列运算结果直接写成幂的形式:
; ;
②将一个非零有理数a的圈n次方写成幂的形式为;
③将 (m为大于等于2的整数)写成幂的形式为 .