安徽合肥庐阳四十五中2021-2022学年九年级上学期数学第一次月考试卷

试卷更新日期：2021-10-12 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）

1. 已知函数y＝（m＋3）x²＋4是二次函数，则m的取值范围为（）

A、m＞－3 B、m＜－3 C、m≠－3 D、任意实数

查看试题解析
2. 对于二次函数y=-2（x+3）²的图象，下列说法正确的是（）

A、开口向上 B、对称轴是直线x=-3 C、当x＞-4时，y随x的增大而减小 D、顶点坐标为（-2，-3）

查看试题解析
3. 已知二次函数y=-x²+bx+c的顶点为（1，5），那么关于x的一元二次方程-x²+bx+c-4=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
4. 已知二次函数y=x²-6x+8，当0<x≤m时，-1≤y≤8，则m的值是（）

A、3 B、4 C、6 D、7

查看试题解析
5. 我们定义两个不相交的函数图象在竖直方向上的最短距离为这两个函数的“和谐值”．抛物线y=x²-2x+3与直线y=x-2的“和谐值”为（）

A、3 B、 $\frac{11}{4}$ C、 $\frac{5}{2}$ D、2

查看试题解析
6. 定义：min{a，b}= ${\begin{cases} a (a \leq b) \\ b (a > b) \end{cases}$ ，若函数y=min{x+1，-x²+2x+3}，则该函数的最大值为（）

A、0 B、2 C、3 D、4

查看试题解析
7. 已知点A（x₁ ， y₁），B（x₂ ， y₂）都在反比例函数 $y = - \frac{3}{x}$ 的图象上，且x₁< 0< x₂ ，则y₁ ， y₂的关系是（）

A、y₁> y₂ B、y₁< y₂ C、y₁=y₂ D、|y₁|=|y₂|

查看试题解析
8. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长），其余三边除大门外用栅栏围成，栅栏总长度为50m，门宽为2m．若饲养室长为xm，占地面积为ym² ，则y关于x的函数表达式为（）

A、y=- $\frac{1}{2}$ x²+26x（2≤x＜52） B、y=- $\frac{1}{2}$ x²+50x（2≤x＜52） C、y=-x²+52x（2≤x＜52） D、y=- $\frac{1}{2}$ x²+27x-52（2≤x＜52）

查看试题解析
9. 抛物线y=-x²+bx+3的对称轴为直线x=-1，若关于x的一元二次方程-x²+bx+3-t=0（t为实数）在-2＜x＜3的范围内有实数根，则t的取值范围是（）

A、-12＜t≤3 B、-12＜t＜4 C、-12＜t≤4 D、-12＜t＜3

查看试题解析
10. 二次函数y=ax²+bx+c(a≠0)的部分图象如图4所示，图象过点（-4，0），对称轴为直线x=-1。有下列结论：①abc>0；②2a-b=0；③一元二次方程ax²+bx+c=0的解是x₁=-4，x₂=1；④当y>0时，-4< x< 2。其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共4小题，每小题5分，满分20分）

11. 已知二次函数y=x²+（m-2）x-2m，当m=时，函数图象的顶点在x轴上．

查看试题解析
12. 飞机着陆后滑行的距离s（单位：m）与滑行的时间t（单位：s）的函数解析式是s=60t-1.5t² ，那么飞机着陆后滑行s时间才能停下来。

查看试题解析
13. 根据表格估计方程x²+2x=6其中一个解的近似值．

x

1.63

1.64

1.65

1.66

…

x²+2x

5.9169

5.9696

6.0225

6.0756

…

根据上表，求方程x²+2x=6的一个解大约是（精确到0.01）

查看试题解析
14. 如图，抛物线y= - $\frac{1}{2}$ x²+ $\frac{3}{2}$ x+2与x轴交于点A，B(点B在点A的左侧），与y轴交于点C，连接BC，AC.

(1)、∠ACB的度数是°；

(2)、若点P是AC上一动点，则OP的最小值为.

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 已知函数y=（|m|-1）x²+（m+1)x+3.

(1)、若这个函数是一次函数，求m的值；

(2)、若这个函数是二次函数，求m的取值范围.

查看试题解析
16. 已知抛物线的顶点为(-1，4)，且经过点(2，-5)，试确定该抛物线的函数表达式.

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 如图，抛物线y=2x²-6x+4与x轴交于A，B两点(点A在点B左侧)，与y轴交于C.

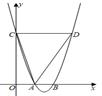(1)、求点A、点C的坐标；

(2)、作 CD∥x轴交抛物线于D，连接AC，AD，求△ACD的面积.；

查看试题解析
18. 已知二次函数y= -x²+2x+3.

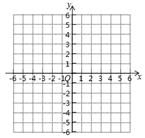(1)、在坐标系中作出该函数的图象；

(2)、结合图象，①直接写出函数图象与x轴的交点坐标；
②直接写出不等式 –x²+2x+3< 0的解集.

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 为应对全球爆发的新冠疫情，某疫苗生产企业于2021年1月份开始了技术改造，其月生产数量y(万支)与月份x之间的变化如图所示，技术改造完成前是反比例函数图象的一部分，技术改造完成后是一次函数图象的一部分，请根据图中数据解答下列问题：

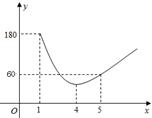(1)、该疫苗生产企业4月份的生产数量为多少万支？

(2)、该疫苗生产企业有多少个月的月生产数量不超过90万支？

查看试题解析
20. 已知二次函数y= -x²+2x-m（m是常数)﹒

(1)、若该二次函数的图象与x轴有两个不同的交点，求m的取值范围；

(2)、若该二次函数的图象与x轴的其中一个交点坐标为(-1，0)，求一元二次方程 -x²+2x-m=0的解.

查看试题解析

六、（本题满分12分）

21. 如图，一次函数y= $\frac{3}{4}$ x-3的图象与坐标轴交于点A、B，二次函数y= $\frac{3}{8}$ x²+bx+c的图象过A、B两点.

(1)、求二次函数的表达式；

(2)、已知点Р在对称轴上，且点P位于x轴上方，连接PB，若PB=AB，求点P的坐标.

查看试题解析

七、（本题满分12分）

22. 为巩固“脱贫攻坚”成果，某驻村干部指导农户进行草莓种植和销售，已知草莓的种植成本为8元/千克，经市场调查发现，今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8<x≤32)成一次函数关系，下表列出了x与y的一些对应值：

(1)、根据表中信息，求y与x的函数关系式；

(2)、若五一期间销售草毒获取的利润为w(元)，请写出w与x之间函数表达式，并求出销售单价为多少时，获得的利润最大?最大利润是多少?（利润=销售额一成本)

查看试题解析

八、（本题满分14分）

23. 如图，在平面直角坐标系xOy中，一次函数y=k₁x+b的图象与反比例函数y= $\frac{k_{2}}{x}$ 的图象交于点A（2，4)和点B(m，-2）

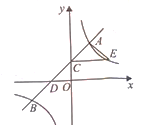(1)、求一次函数与反比例函数的表达式；

(2)、直线AB与x轴交于点D，与y轴交于点C.
①过点C作CE//x轴交反比例函数y= $\frac{k_{2}}{x}$ 多的图象于点E，连接AE，试判断△ACE的形状，并说明理由；

②设M是x轴上一点，当∠CMO= $\frac{1}{2}$ ∠DCO时，求点M的坐标

查看试题解析

x	1.63	1.64	1.65	1.66	…
x²+2x	5.9169	5.9696	6.0225	6.0756	…