炎德英才联考合作体2021-2022学年高三上学期数学10月联考试卷

试卷更新日期：2021-10-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知全集为R，集合 $A = {x | 0 < x < 1}$ ， $B = {x | x > 3}$ ，则（）

A、 $A \subseteq B$ B、 $B \subseteq A$ C、 $A \cup B = R$ D、 $A \cap (C_{R} B) = A$

查看试题解析
2. 等比数列 ${a_{n}}$ 中， $a_{1} + a_{2} = 1 ， a_{4} + a_{5} = - 8$ ，则 $\frac{a_{7} + a_{8}}{a_{5} + a_{6}} =$ （）

A、-8 B、-4 C、2 D、4

查看试题解析
3. 复数 $\frac{{(1 - i)}^{2}}{1 + i} =$ （）

A、 $1 - i$ B、 $- 1 - i$ C、 $1 + i$ D、 $- 1 + i$

查看试题解析
4. 已知平面向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为60°， $\vec{a} = (2 ， 0)$ ， $| \vec{b} | = 1$ ，则 $| \vec{a} - 2 \vec{b} |$ 的值为（）

A、 $\sqrt{2}$ B、2 C、4 D、 $\frac{1}{2}$

查看试题解析
5. 函数 $f (x) = (x^{2} - 2 x) e^{x}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
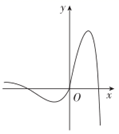6. 非零向量 $\vec{A B}$ ， $\vec{A C}$ 满足 $(\frac{\vec{A B}}{| \vec{A B} |} + \frac{\vec{A C}}{| \vec{A C} |}) \cdot \vec{B C} = 0$ ，且 $\frac{\overset{⇀}{A B}}{| \overset{⇀}{A B} |} \cdot \frac{\overset{⇀}{A C}}{| \overset{⇀}{A C} |} = \frac{1}{2}$ ，则 $△ A B C$ 为（）

A、三边均不相等的三角形 B、直角三角形 C、等腰非等边三角形 D、等边三角形

查看试题解析
7. Logistic模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 $I (t)$ （ $t$ 的单位：天）的Logistic模型： $I (t) = \frac{K}{1 + e^{- 0.23 (t - 52)}}$ 其中 $K$ 为最大确诊病例数．当 $I (t^{*}) = 0.95 K$ 时，标志着已初步遏制疫情，则 $t^{*}$ 约为（） $(\ln 19 \approx 3)$

A、60 B、65 C、66 D、69

查看试题解析
8. 在 $△ A B C$ 中，D为三角形所在平面内一点，且 $\vec{A D} = \frac{1}{3} \vec{A B} + \frac{1}{2} \vec{A C}$ ，则 $\frac{S_{△ B C D}}{S_{△ A C D}} =$ （）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析

二、多选题

9. 设向量 $\vec{a} = (2, 0)$ ， $\vec{b} = (1, 1)$ ，则（）

A、 $| \vec{a} | = | \vec{b} |$ B、 $(\vec{a} - \vec{b}) // \vec{b}$ C、 $(\vec{a} - \vec{b}) ⊥ \vec{b}$ D、 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{4}$

查看试题解析
10. 下列命题错误的是（）

A、命题“ $\exists x_{0} \in R$ ， $x_{0}^{2} + 1 > 3 x_{0}$ ”的否定是“ $\forall x \in R$ ， $x^{2} + 1 > 3 x$ ” B、“函数 $f (x) = \cos a x - \sin a x$ 的最小正周期为 $π$ ”是“ $a = 2$ ”的必要不充分条件 C、 $x^{2} + 2 x \geq a x$ 在 $x \in [1 ， 2]$ 时有解 $\Leftrightarrow {(x^{2} + 2 x)}_{\min} \geq {(a x)}_{\min}$ 在 $x \in [1 ， 2]$ 时成立 D、“平面向量 $\vec{a}$ 与 $\vec{b}$ 的夹角是钝角”的充分必要条件是“ $\vec{a} \cdot \vec{b} < 0$ ”

查看试题解析
11. 有下面四个不等式，其中恒成立的有（）

A、 $\frac{a + b}{2} > \sqrt{a b}$ B、 $a (1 - a) \leq \frac{1}{4}$ C、 $a^{2} + b^{2} + c^{2} \geq a b + b c + c a$ D、 $\frac{b}{a} + \frac{a}{b} \geq 2$

查看试题解析
12. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，下列说法正确的是（）

A、若 $S_{n} = {(n + 1)}^{2}$ ，则 ${a_{n}}$ 是等差数列 B、若 $S_{n} = 2^{n} - 1$ ，则 ${a_{n}}$ 是等比数列 C、若 ${a_{n}}$ 是等差数列，则 $S_{2 n - 1} = (2 n - 1) a_{n}$ D、若 ${a_{n}}$ 是等比数列，则 $S_{n}$ ， $S_{2 n} - S_{n}$ ， $S_{3 n} - S_{2 n}$ 成等比数列

查看试题解析

三、填空题

13. 已知 $a_{n} = \lg \frac{n + 1}{n} (n \in N^{*})$ ，若数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} = 1$ ，则 $n =$

查看试题解析
14. 已知函数 $f (x) = \frac{1}{3} x^{3} + m x^{2} + n x + 1$ 的单调递减区间是 $(- 3 ， 1)$ ，则 $m + n$ 的值为.

查看试题解析
15. 已知对任意平面向量 $\vec{A B} = (x ， y)$ ，把 $\vec{A B}$ 绕其起点沿逆时针方向旋转 $θ$ 角得到向量 $\vec{A P} = (x \cos θ - y \sin θ ， x \sin θ + y \cos θ)$ ，叫做把点B绕点A沿逆时针方向旋转 $θ$ 角得到点P.已知平面内点 $A (- \frac{3}{2} \sqrt{3} ， 2 \sqrt{3})$ ， $B (4 - \frac{3}{2} \sqrt{3} ， 3 + 2 \sqrt{3})$ ，把点B绕点A沿顺时针方向旋转 $\frac{π}{3}$ 后得到点P，则点P的坐标为.

查看试题解析
16. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，若 $A - C = \frac{π}{2}$ ，a，b，c成等差数列，则 $\cos B$ 的值为．

查看试题解析

四、解答题

17. 在△ABC中，角A，B，C所对的边分别为a，b，c，设S为△ABC的面积，满足 $S = \frac{\sqrt{3}}{4} (a^{2} + b^{2} - c^{2})$ ．
（Ⅰ）求角C的大小；

（Ⅱ）求 $\sin A + \sin B$ 的最大值．

查看试题解析
18. 某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本 $y$ 万元与年产量 $x$ 吨之间的函数关系可以近似地表示为 $y = \frac{x^{2}}{5} - 24 x + 2000$ ，已知此生产线的年产量最小为60吨，最大为110吨.

(1)、年产量为多少吨时，生产每吨产品的平均成本最低?并求最低平均成本；

(2)、若每吨产品的平均出厂价为24万元，且产品能全部售出，则年产量为多少吨时，可以获得最大利润?并求最大利润.

查看试题解析
19. 已知在数列 ${a_{n}}$ 中， $a_{1} = 3$ ， $a_{n} = a_{n - 1} + 2^{n - 1} (n \geq 2)$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \log_{2} (a_{n + 1} - 1)$ ，求 ${\frac{1}{b_{n} b_{n + 1}}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
20. 已知函数 $f (x) = x \ln x + (1 - a) x + a$ .

(1)、当 $a = 0$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、若对任意 $x \in (0 ， 1)$ ，不等式 $f (x) > 0$ 恒成立，求正整数 $a$ 的最小值.

查看试题解析
21. 已知函数 $f (x) = \sqrt{3} \sin (ω x + φ) + 2 \sin^{2} (\frac{ω x + φ}{2}) - 1$ （ $ω > 0$ ， $0 < φ < π$ ）为奇函数，且 $f (x)$ 图象的相邻两对称轴间的距离为 $\frac{π}{2}$ .

(1)、求 $f (x)$ 的解析式与单调递减区间；

(2)、将函数 $f (x)$ 的图象向右平移 $\frac{π}{6}$ 个单位长度，再把横坐标缩小为原来的 $\frac{1}{2}$ （纵坐标不变），得到函数 $y = g (x)$ 的图象，当 $x \in [- \frac{π}{12} ， \frac{π}{6}]$ 时，求函数 $g (x)$ 的值域.

查看试题解析
22. 已知函数 $f (x) = e^{x} - \frac{1}{2} x^{2} - a x (a \in R)$ ．

(1)、若函数 $f (x)$ 在R上是增函数，求实数a的取值范围；

(2)、如果函数 $g (x) = f (x) - (a - \frac{1}{2}) x^{2}$ 恰有两个不同的极值点 $x_{1} ， x_{2}$ ，证明： $\frac{x_{1} + x_{2}}{2} < \ln 2 a$ ．

查看试题解析