福建省普通高中2022届高三数学9月阶段性质量检测试卷

试卷更新日期：2021-10-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {1, 2, 3},$ $B = {x | x^{2} < 9}$ ，则 $A \cap B =$ （）

A、 ${- 2, - 1, 0, 1, 2, 3}$ B、 ${- 2, - 1, 0, 1, 2}$ C、 ${1,2,3}$ D、 ${1, 2}$

查看试题解析
2. 已知等差数列{a_n}前9项的和为27，a₁₀=8，则a₁₀₀=（　　）

A、100 B、99 C、98 D、97

查看试题解析
3. 若 $\cos (\frac{π}{4} - α) = \frac{3}{5}$ ，则 $\sin 2 α =$ （）

A、 $\frac{7}{25}$ B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、 $- \frac{7}{25}$

查看试题解析
4. 下列函数中，在区间 $(- 1 ， 1)$ 上为减函数的是（）

A、 $y = \frac{2020}{2000 - x}$ B、 $y = \cos x$ C、 $y = \ln (x + 1)$ D、 $y = 2021^{- x}$

查看试题解析
5. 设{a_n}是首项为正数的等比数列，公比为q ，则“q<0”是“对任意的正整数n ， a_2n₋₁+a_2n<0”的（）

A、充要条件 B、充分而不必要条件 C、必要而不充分条件 D、既不充分也不必要条件

查看试题解析
6. 函数 $f (x) = \frac{x^{2} \sin | x |}{e^{x}}$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
7. 已知 $a = 5^{\sqrt{2}}$ ， $b = \log_{2} 37$ ， $c = \ln (e^{6} + 50)$ ，则（）

A、 $b < a < c$ B、 $a < b < c$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析
8. 已知椭圆C₁： $\frac{x^{2}}{m^{2}}$ +y²=1（m＞1）与双曲线C₂： $\frac{x^{2}}{n^{2}}$ –y²=1（n＞0）的焦点重合，e₁ ， e₂分别为C₁ ， C₂的离心率，则（）

A、m＞n且e₁e₂＞1 B、m＞n且e₁e₂＜1 C、m＜n且e₁e₂＞1 D、m＜n且e₁e₂＜1

查看试题解析
9. 若 $\tan θ = \sqrt{3}$ ，则 $\cos 2 θ =$ （）

A、 $\frac{1}{2}$ B、-0.5 C、 $- \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析

二、多选题

10. 已知 $p$ ：关于 $x$ 的不等式 $m x^{2} - 2 x + 1 > 0$ 的解集为 $R$ ，则下列结论正确的是（）

A、 $p$ 的必要不充分条件是 $0 \leq m$ B、 $p$ 的充分不必要条件是 $m = 2020$ C、 $1 < m$ 是 $p$ 的充要条件 D、 $| m | \leq 1$ 是 $p$ 的既不充分也不必要条件

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} x^{2} + (4 a - 3) x + 3 a ， x < 0 \\ \log_{a} (x + 1) + 1 ， x \geq 0 \end{array}$ （ $a > 0$ 且 $a \neq 1$ ）在 $R$ 上单调递减，且关于 $x$ 的方程 $| f (x) | = 2 - \frac{x}{3}$ 有2个不相等的实数解，则 $a$ 的取值可以是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 设 $x > 0$ ， $x ， y \in R$ ，则（）

A、“ $x > y$ ” $\Rightarrow$ “ $x > | y |$ ” B、“ $x < y$ ” $\Rightarrow$ “ $x < | y |$ ” C、“ $x \geq | y |$ ” $\Rightarrow$ “ $x + y \geq | x + y |$ ” D、“ $x > y$ ” $\Rightarrow$ “ $x + | y | \geq | x + y |$ ”

查看试题解析

三、填空题

13. 已知曲线 $f (x) = x^{3} + b$ 在 $x = a (a > 0)$ 处的切线方程为 $3 x - y + 2 = 0$ ，则 $b =$ .

查看试题解析
14. 方程 $3 \cos 2 x = \sin x + 1$ 在区间 $[0 ， π]$ 上的解为．

查看试题解析
15. 已知 ${a_{n}}$ 为等差数列， $S_{n}$ 为其前 $n$ 项和，若 $a_{1} = 4$ ， $a_{3} + a_{5} = 0$ ，则 $S_{6} =$ ．

查看试题解析
16. 已知函数 $f (x)$ 是定义在R上的周期为2的奇函数，当0＜x＜1时， $f (x) = 3^{x}$ ，则 $f (- \frac{5}{2}) + f (1)$ = ．

查看试题解析

四、解答题

17. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别是 $a$ ， $b$ ， $c$ ，且 $\frac{\cos A}{a} + \frac{\cos B}{b} = \frac{\sin C}{c}$ ．

(1)、证明： $\sin A \sin B = \sin C$ ；

(2)、若 $\cos A = \frac{3}{5}$ ，求 $\sin B$ ．

查看试题解析
18. 某化肥厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料．生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示：

原料

肥料

A

B

C

甲

4

8

3

乙

5

5

10

现有A种原料400吨，B种原料460吨，C种原料500吨，在此基础上生产甲乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元．分别用x，y表示生产甲、乙两种肥料的车皮数．

(1)、用x，y列出满足生产条件的数学关系式；

(2)、问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．

查看试题解析
19. 等差数列{a_n}中，a₃+a₄=4，a₅+a₇=6．

(1)、求{a_n}的通项公式；

(2)、设b_n=[a_n]，求数列{b_n}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0，[2.6]=2．

查看试题解析
20. 将边长为1的正方形 $A A_{1} O_{1} O$ （及其内部）绕 $O O_{1}$ 旋转一周形成圆柱，如图， $\overset{⌢}{A C}$ 长为 $\fr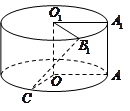ac{2 π}{3}$ ， $\overset{⌢}{A_{1} B_{1}}$ 长为 $\frac{π}{3}$ ，其中 $B_{1}$ 与 $C$ 在平面 $A A_{1} O_{1} O$ 的同侧.

(1)、求三棱锥 $C - O_{1} A_{1} B_{1}$ 的体积；

(2)、求异面直线 $B_{1} C$ 与 $A A_{1}$ 所成的角的大小.

查看试题解析
21. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ ( $a > 0$ ， $b > 0$ )的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，双曲线的 $C$ 右顶点 $A$ 在圆 $O$ ： $x^{2} + y^{2} = 1$ 上，且 $\vec{A F_{1}} \cdot \vec{A F_{2}} = - 1$ ．

(1)、求双曲线 $C$ 的标准方程；

(2)、动直线 $l$ 与双曲线 $C$ 恰有1个公共点，且与双曲线 $C$ 的两条渐近线分别交于点 $M$ 、 $N$ ，问 $△ O M N$ ( $O$ 为坐标原点)的面积是否为定值？若为定值，求出该定值；若不为定值，试说明理由．

查看试题解析
22. 已知函数 $f (x) = (x - 2) e^{x} + a {(x - 1)}^{2}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 有两个零点，求 $\frac{\sqrt{a}}{a + 1}$ 的取值范围．

查看试题解析