福建省龙岩市重点高中2022届高三上学期数学第一次月考试卷

试卷更新日期：2021-10-11 类型：月考试卷

进入出卷网下载

一、单选题

1. 设集合 $A = {x | \frac{1}{2} \leq 2^{x} \leq 8} ， B = {x | y = \ln (2 - x)}$ ，则 $A \cap B =$ （）

A、 $[- 3 ， 2)$ B、 $(2 ， 3]$ C、 $[- 1 ， 2)$ D、 $(- 1 ， 2)$

查看试题解析
2. 下列函数中，既为奇函数又在定义域内单调递增的是（）

A、 $y = 2^{- x} - 2^{x}$ B、 $y = \log_{2} (x^{2} + 1)$ C、 $y = \ln (\frac{1 + x}{1 - x}) + x$ D、 $y = | \sin x |$

查看试题解析
3. 牛顿曾经提出了常温环境下的温度冷却模型： $t = - \frac{1}{k} \ln \frac{θ - θ_{0}}{θ_{1} - θ_{0}}$ （ $t$ 为时间，单位分钟， $θ_{0}$ 为环境温度， $θ_{1}$ 为物体初始温度， $θ$ 为冷却后温度），假设一杯开水温度 $θ_{1} = 100$ ℃，环境温度 $θ_{0} = 20$ ℃，常数 $k = 0.2$ ，大约经过多少分钟水温降为40℃？（结果保留整数，参考数据： $\ln 2 \approx 0.7$ ）（）

A、9 B、8 C、7 D、6

查看试题解析
4. 函数 $f (x) = \frac{e^{x} - e^{- x}}{x^{2}}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
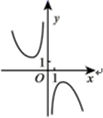5. 下列命题中为真命题的是（）

A、“ $a - b = 0$ ”的充要条件是“ $\frac{a}{b} = 1$ ” B、“ $a > b$ ”是“ $\frac{1}{a} < \frac{1}{b}$ ”的充分不必要条件 C、命题“ $\exists x \in R$ ， $x^{2} - 2^{x} < 0$ ”的否定是“ $\forall x \in R$ ， $x^{2} - 2^{x} \geq 0$ ” D、“ $a > 2$ ， $b > 2$ ”是“ $a b > 4$ ”的必要条件

查看试题解析
6. 已知函数f(x)是偶函数，且f(x)在 $[0 ， + \infty)$ 上是增函数，若 $f (\frac{1}{2}) = 0$ ，则不等式 $f (\log_{4} x) > 0$ 的解集为（）

A、{x|x>2} B、 ${x | 0 < x < \frac{1}{2}}$ C、{ $x | 0 < x < \frac{1}{2}$ 或x>2} D、{ $x | \frac{1}{2} < x < 1$ 或x>2}

查看试题解析
7. 已知 $a > 0 ， b > 0$ ，且 $a + b = 1$ ，则 $\frac{3 a b}{a + 4 b}$ 的最大值为（）

A、 $\frac{3}{10}$ B、 $\frac{3}{8}$ C、 $\frac{9}{28}$ D、 $\frac{1}{3}$

查看试题解析
8. 已知函数 $f (x) = x^{2} - b x + c$ 满足 $f (1 + x) = f (1 - x)$ ，且 $f (0) = 3$ ，则 $f (b^{x})$ 与 $f (c^{x})$ 的大小关系为（）

A、 $f (c^{x}) \geq f (b^{x})$ B、 $f (c^{x}) \leq f (b^{x})$ C、 $f (c^{x}) > f (b^{x})$ D、 $f (c^{x}) = f (b^{x})$

查看试题解析

二、多选题

9. 已知集合 $A = {x \in R | x^{2} - 3 x - 18 < 0}$ ， $B = {x \in R | x^{2} + a x + a^{2} - 27 < 0}$ ，则下列命题中正确的是（）

A、若 $A = B$ ，则 $a = - 3$ B、若 $A \subseteq B$ ，则 $a = - 3$ C、若 $B = \emptyset$ ，则 $a \leq - 6$ 或 $a \geq 6$ D、若 $B ⊊ A$ 时，则 $- 6 < a \leq - 3$ 或 $a \geq 6$

查看试题解析
10. 已知 $x > 0$ ， $y > 0$ ，且 $2 x + y = 1$ ，则 $\frac{x + 1}{x y}$ 可能取的值有（）

A、9 B、10 C、11 D、12

查看试题解析
11. 已知函数 $f (x) = x^{2} - 2 (a - 1) x + a$ ，若对于区间 $[- 1, 2]$ 上的任意两个不相等的实数 $x_{1}$ ， $x_{2}$ ，都有 $f (x_{1}) \neq f (x_{2})$ ，则实数 $a$ 的取值范围可以是（）

A、 $(- \infty, 0]$ B、 $[0, 3]$ C、 $[- 1, 2]$ D、 $[3, + \infty)$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} x + 2 & x \leq 0 \\ | lg x | & x > 0 \end{array}$ ，方程 $f^{2} (x) - m f (x) - 1 = 0$ 有4个不同的实数根，则下列选项正确的为（）

A、函数 $f (x)$ 的零点的个数为2 B、实数 $m$ 的取值范围为 $(- \infty ， \frac{3}{2}]$ C、函数 $f (x)$ 无最值 D、函数 $f (x)$ 在 $(0 ， + \infty)$ 上单调递增

查看试题解析

三、填空题

13. 计算求值： ${(\frac{1}{4})}^{\frac{1}{2}} - {(π - 3)}^{0} + {(\frac{1}{27})}^{- \frac{2}{3}} + \lg 5 + \lg 2 + e^{\ln 2} + \frac{1}{4} \lg 0.01 =$ .

查看试题解析
14. 若函数 $f (x) = {log}_{4} (4^{x} + 1) - k x$ 为偶函数，则 $k =$ .

查看试题解析
15. 已知函数 $f (x) = \log_{a} (2 x - a)$ 在区间 $[\frac{1}{3} ， \frac{2}{3}]$ 上恒有 $f (x) > 0$ ，则实数 $a$ 的取值范围为.

查看试题解析
16. 设函数 $f (x) = {\begin{array}{l} x^{2} - 2 x + 2 ， (x \geq 0) \\ \log_{2} (x + 2) + 1 ， (- 2 < x < 0) \end{array}$ ，若互不相等的实数 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 满足 $f (x_{1}) = f (x_{2}) = f (x_{3})$ ，则 $x_{1} + x_{2} + x_{3}$ 的取值范围是．

查看试题解析

四、解答题

17. 已知集合 $A = {x | x^{2} - 2 x + m \leq 0}$ ， $B = {y | y = 3^{x} ， x \leq n}$ .

(1)、若集合A为空集，求实数m的取值范围：

(2)、当 $m = - 8$ 时，若“ $x \in A$ ”是“ $x \in B$ ”的必要不充分条件，求实数n的取值范围.

查看试题解析
18. 已知函数 $f (x) = x^{2} + a x - a - 1 (a \in R)$ .

(1)、若 $f (x)$ 在 $[1, + \infty)$ 上单调递增，求a的取值范围；

(2)、解关于x的不等式 $f (x) \leq 0$ .

查看试题解析
19. 已知函数 $f (x) = \frac{2^{x} - a}{2^{x} + 1}$ 为奇函数.

(1)、求实数 $a$ 的值并证明 $f (x)$ 的单调性；

(2)、若实数满足不等式 $f (\frac{1}{t - 2}) + f (- 1) > 0$ ，求 $t$ 的取值范围.

查看试题解析
20. 已知函数 $f (x) = a^{x} + \log_{a} x (a > 0 ， a \neq 1)$ 在 $[1 ， 2]$ 上的最大值与最小值之和为 $6 + \log_{a} 2$ ．

(1)、求实数 $a$ 的值；

(2)、对于任意的 $x \in [2 ， + \infty)$ ，不等式 $k f (x) - 1 \geq 0$ 恒成立，求实数 $k$ 的取值范围．

查看试题解析
21. 已知函数 $f (x)$ 为 $R$ 上的偶函数， $g (x)$ 为 $R$ 上的奇函数，且 $f (x) + g (x) = \log_{4} (4^{x} + 1)$ ．

(1)、求 $f (x)$ ， $g (x)$ 的解析式；

(2)、若函数 $h (x) = f (x) - \frac{1}{2} \log_{2} (a \cdot 2^{x} + 2 \sqrt{2} a)$ （ $a > 0$ ）在 $R$ 上只有一个零点，求实数 $a$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = x^{2} + (m - 2) x - m$ ， $g (x) = \frac{f (x)}{x}$ ，且函数 $y = f (x - 2)$ 是偶函数.

(1)、若不等式 $g (\ln x) - n \ln x \geq 0$ 在 $[\frac{1}{e^{2}} ， 1)$ 上恒成立，求 $n$ 的取值范围；

(2)、若函数 $y = g [\log_{2} (x^{2} + 4)] + k \cdot \frac{2}{\log_{2} (x^{2} + 4)} - 9$ 恰好有三个零点，求 $k$ 的值及该函数的零点.

查看试题解析