北师版数学八年级上册《第三章 位置与坐标》单元检测B卷
试卷更新日期:2021-10-09 类型:单元试卷
一、单选题
-
1. 在平面直角坐标系中,若点P(a-3,1)与点Q(2,b+1)关于x轴对称,则a+b的值是( )A、1 B、2 C、3 D、42. 在平面直角坐标系中,点 关于原点对称的点的坐标是( )A、(-3,2) B、(3,-2) C、(-2,-3) D、(-3,-2)3. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=-3,n=2 C、m=3,n=2 B.m=-2,n=34. 在平面直角坐标系中,点P(-3,m2+1)关于原点对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图的坐标平面上有原点O与A,B,C,D四点.若有一直线L通过点(-3,4)且与y轴垂直,则L也会通过下列哪一点?( )
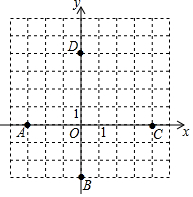 A、A B、B C、C D、D6. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、7. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、78. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
A、A B、B C、C D、D6. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、7. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、78. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
A、(4,1) B、(﹣1,4) C、(﹣4,﹣1) D、(﹣1,﹣4)9. 在平面直角坐标系中,第四象限内有一点M,它到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、(-4,5) B、(-5,4) C、(4,-5) D、(5,-4)10. 如图所示,在平面直角坐标系中,点P(-1,2)关于直线x=1的对称点的坐标为( ) A、(1,2) B、(2,2) C、(3,2) D、(4,2)11. 在直角坐标系中,点A(1,2)的横坐标乘-1,纵坐标不变,得到A'点,则点A与点A'的关系是( )A、关于x轴对称 B、关于y轴对称 C、没有对称关系 D、将A点向x轴的负方向平移1个单位长度12. 已知点P(m+2,2m-4)在x轴上,则点P的坐标是( )A、(4,0) B、(0,4) C、(-4,0) D、(0,-4)
A、(1,2) B、(2,2) C、(3,2) D、(4,2)11. 在直角坐标系中,点A(1,2)的横坐标乘-1,纵坐标不变,得到A'点,则点A与点A'的关系是( )A、关于x轴对称 B、关于y轴对称 C、没有对称关系 D、将A点向x轴的负方向平移1个单位长度12. 已知点P(m+2,2m-4)在x轴上,则点P的坐标是( )A、(4,0) B、(0,4) C、(-4,0) D、(0,-4)二、填空题
-
13. 如图,在直角坐标系中,已知点 ,将 绕点 逆时针方向旋转 后得到 ,则点 的坐标是.
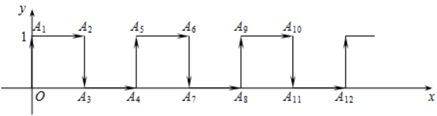
 14. 已知点A( , )与点B( , )关于 轴对称,则 =.15. 点N(a+5,a-2)在y轴上,则点N的坐标为16. 如图,动点P从坐标原点 出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点 ,第2秒运动到点 ,第3秒运动到点 ,第4秒运动到点 …则第2068秒点P所在位置的坐标是.
14. 已知点A( , )与点B( , )关于 轴对称,则 =.15. 点N(a+5,a-2)在y轴上,则点N的坐标为16. 如图,动点P从坐标原点 出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点 ,第2秒运动到点 ,第3秒运动到点 ,第4秒运动到点 …则第2068秒点P所在位置的坐标是.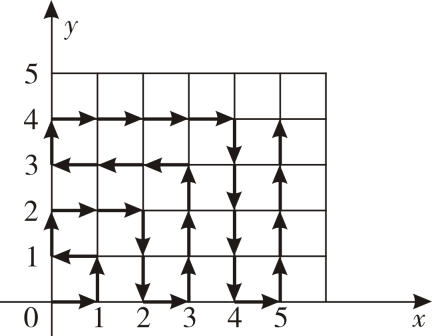 17. 点P位于x轴下方,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是18. 在平面直角坐标系中,点P( , )到原点的距离是。
17. 点P位于x轴下方,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是18. 在平面直角坐标系中,点P( , )到原点的距离是。三、解答题
-
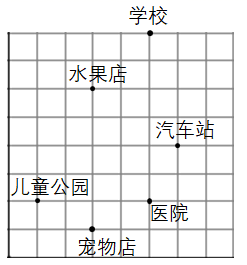
19. 请在图中建立平面直角坐标系,使学校的坐标是 ,并写出儿童公园,医院,水果店,宠物店,汽车站的坐标.
 20. 已知点 ,根据下列条件,求出点 的坐标.(1)、点 在 轴上;(2)、点 的坐标为 ,直线 轴.21. 如图, 在平面直角坐标系中的坐标分别为 , ,
20. 已知点 ,根据下列条件,求出点 的坐标.(1)、点 在 轴上;(2)、点 的坐标为 ,直线 轴.21. 如图, 在平面直角坐标系中的坐标分别为 , ,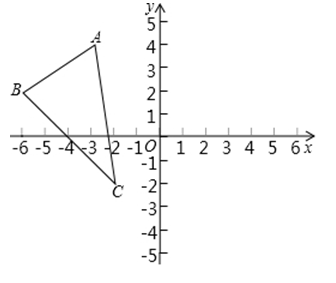 (1)、作出 关于y轴对称的图形 ;(2)、分别求出 、 、 的坐标.22. 作图题:
(1)、作出 关于y轴对称的图形 ;(2)、分别求出 、 、 的坐标.22. 作图题:如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
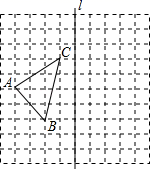
( 1 )在图中画出△ABC关于直线l对称的△A1B1C1;
(要求:A与A1 , B与B1 , C与C1相对应)
( 2 )求出△A1B1C1面积.
( 3 )在直线l上找一点P,使得PA+PB的值最小.
23. 问题情境:在平面直角坐标系 中有不重合的两点 和点 ,小明在学习中发现,若 ,则 轴,且线段 的长度为 ;若 ,则 轴,且线段 的长度为 ;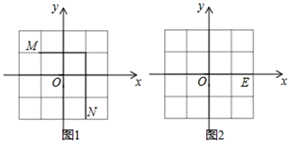 (1)、(应用)
(1)、(应用)若点 、 ,则 轴, 的长度为 .
(2)、若点 ,且 轴,且 ,则点 的坐标为 .(3)、(拓展)我们规定:平面直角坐标系中任意不重合的两点 , 之间的折线距离为 ;例如:图1中,点 与点 之间的折线距离为 .
解决下列问题:
如图1,已知 ,若 ,则 =;
(4)、如图2,已知 , ,若 ,求t的值.