天津市南开区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下面图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，是随机事件的是（）

A、画一个三角形，其内角和是180° B、投掷一枚正六面体骰子，朝上一面的点数为5 C、在只装了红色卡片的袋子里，摸出一张白色卡片 D、明天太阳从东方升起

查看试题解析
3. 对于反比例函数y= $\frac{3}{x}$ ，下列判断正确的是（）

A、图象经过点(-1，3) B、图象在第二、四象限 C、不论x为何值，y>0 D、图象所在的第一象限内，y随x的增大而减小

查看试题解析
4. 如图，四边形ABCD是正方形，点E、F分别在线段BC、DC上，∠BAE＝25°，若线段AE绕点A逆时针旋转后与线段AF重合，则旋转的角度是（）

A、25° B、40° C、90° D、50°

查看试题解析
5. 如图，在△ABC中，DE∥BC，AD＝6，DB＝3，AE＝4，则AC的长为（）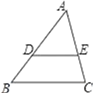

A、2 B、4 C、6 D、8

查看试题解析
6. 如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（）

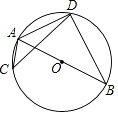A、∠ADC B、∠ABD C、∠BAC D、∠BAD

查看试题解析
7. 已知 $A (x_{1}, y_{1}), B (x_{2}, y_{2}), C (x_{3}, y_{3})$ 是反比例函数 $y = \frac{2}{x}$ 上的三点，若 $x_{1} < x_{2} < x_{3}$ ， $y_{2} < y_{1} < y_{3}$ ，则下列关系式错误的是（）

A、 $x_{1} x_{2} < 0$ B、 $x_{1} x_{3} < 0$ C、 $x_{2} x_{3} < 0$ D、 $x_{1} + x_{2} < 0$

查看试题解析
8. 已知k₁＜0＜k₂ ，则函数y=k₁x和y= $\frac{k_{2}}{x}$ 的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
9. 如图， $P A$ 切 $⊙ O$ 于点 $A ， P B$ 切 $⊙ O$ 于点 $B ， P O$ 交 $⊙ O$ 于点 $C$ ，下列结论中不一定成立的是（）

A、 $P A = P B$ B、 $P O$ 平分 $∠ A P B$ C、 $A B ⊥ O P$ D、 $∠ P A B = 2 ∠ A P O$

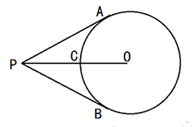查看试题解析
10. 已知二次函数y＝x²﹣（m﹣2）x＋4图象的顶点在坐标轴上，则m的值一定不是（）

A、2 B、6 C、﹣2 D、0

查看试题解析
11. 如图，⊙O的半径为1，点 O到直线 a的距离为2，点 P是直线a上的一个动点，PA切⊙O于点 A，则 PA的最小值是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
12. 如图是抛物线y₁＝ax²＋bx＋c（a≠0）的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点为B（4，0），直线y₂＝mx＋n（m≠0）与抛物线交于A、B两点，结合图象分析下列结论：
①2a＋b＝0；②abc＞0；③方程ax²＋bx＋c＝3有两个相等的实数根；④当1＜x＜4时，有y₂＜y₁；⑤抛物线与x轴的另一个交点是（﹣1，0）．

其中正确的是（）

A、①②③ B、②④ C、①③④ D、①③⑤

查看试题解析

二、填空题

13. 已知 $4 a = 5 b$ ，则 $\frac{a}{b} =$ ．

查看试题解析
14. 现有4条线段，长度依次是2、4、6、7，从中任选三条，能组成三角形的概率是．

查看试题解析
15. 下列y关于x的函数中，y随x的增大而增大的有．（填序号）
①y＝﹣2x+1，②y $= \frac{1}{x}$ ，③y＝（x+2）²+1（x＞0），④y＝﹣2（x﹣3）²﹣1（x＜0）

查看试题解析
16. 如图，菱形 $O A B C$ 的顶点C的坐标为 $(3 ， 4)$ ，顶点A在x轴的正半轴上.反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过顶点B，则k的值为．

查看试题解析
17. 如图，正六边形ABCDEF的边长为2，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为（结果保留根号和π）．

查看试题解析
18. 如图，在由小正方形组成的网格中，△ABC的顶点都在格点上，请借助网格，仅用无刻度的直尺在网格中作出△ABC的高AH，并简要说明作图方法（不要求证明）

查看试题解析

三、解答题

19. 有4个完全相同的小球，把它们分别标号为1、2、3、4，放在一个口袋中，随机的摸出一个小球然后放回，再随机的摸出一个小球.

(1)、采用树形图法（或列表法）列出两次摸球出现的所有可能结果，并回答两次摸球出现的所有可能结果共有几种.

(2)、求两次摸出的球的标号相同的概率；

(3)、求两次摸出的球的标号的和等于4的概率.

查看试题解析
20. 如图，A、B是双曲线 $y = \frac{k}{x}$ 上的点，点A的坐标是（1，4），B是线段AC的中点．

(1)、求k的值；

(2)、求△OAC的面积．

查看试题解析
21. 如图，在等边三角形ABC中，点E为CB边上一点（与点C不重合），点F是AC边上一点，若AB＝5，BE＝2，∠AEF＝60°，求AF的长度．

查看试题解析
22. 在△ABC中， $∠ C = 90^{°}$ ，以边AB上一点O为圆心，OA为半径的圈与BC相切于点D，分别交AB，AC于点E，F

(1)、如图①，连接AD，若 $∠ C A D = 25^{°}$ ，求∠B的大小；

(2)、如图②，若点F为 $\overset{⌢}{A D}$ 的中点， $⊙ O$ 的半径为2，求AB的长．

查看试题解析
23. 如图，一段长为45m的篱笆围成一个一边靠墙的矩形花园，墙长为27m，设花园的面积为sm² ，平行于墙的边为xm．若x不小于17m，

(1)、求出s关于x的函数关系式；

(2)、求s的最大值与最小值．

查看试题解析
24. 平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（ $6$ ， $6$ ），P是射线OB上一点，将 $△ A O P$ 绕点A顺时针旋转90°，得 $△ A B Q$ ，Q是点P旋转后的对应点.

(1)、如图（1）当OP = $2 \sqrt{2}$ 时，求点Q的坐标；

(2)、如图（2），设点P（ $x$ ， $y$ ）（ $0 < x < 6$ ）， $△ A P Q$ 的面积为S. 求S与 $x$ 的函数关系式，并写出当S取最小值时，点P的坐标；

(3)、当BP+BQ = $8 \sqrt{2}$ 时，求点Q的坐标（直接写出结果即可）

查看试题解析
25. 在平面直角坐标系中，设二次函数 $y = x^{2} - x - a^{2} - a$ ，其中 $a > 0$ ；

(1)、若函数y的图象经过点（1，﹣2），求函数y的解析式；

(2)、若抛物线与x轴的两交点坐标为A，B（A点在B点的左侧），与y轴的交点为C，满足OC＝2OB时，求 $a$ 的值．

(3)、已知点 $P (x_{0} ， m)$ 和 $Q (1 ， n)$ 在函数y的图象上，若m＜n，求 $x_{0}$ 的取值范围．

查看试题解析