天津市河东区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $3 x^{2} + 2 x - 3 = 0$ 的一次项系数和常数项分别是（）

A、2和﹣3 B、3和﹣2 C、﹣3和2 D、3和2

查看试题解析
2. 下列关系式中，不是y关于x的反比例函数的是（）

A、xy＝2 B、y＝ $\frac{5 x}{8}$ C、x＝ $\frac{5}{7 y}$ D、x＝5y^﹣1

查看试题解析
3. 抛掷一枚质地均匀的硬币，“反面朝上”的概率为0.5，那么抛掷一枚质地均匀的硬币100次，下列理解正确的是（）

A、可能有50次反面朝上 B、每两次必有1次反面朝上 C、必有50次反面朝上 D、不可能有100次反面朝上

查看试题解析
4. 如图， $⊙ O$ 的半径等于4，如果弦 $A B$ 所对的圆心角等于90°，那么圆心O到弦 $A B$ 的距离为（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、 $3 \sqrt{2}$

查看试题解析
5. 下面图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 已知⊙O的半径OA长为1，OB＝ $\sqrt{2}$ ，则正确图形可能是（）

A、 B、 C、 D、

查看试题解析
7. 如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D。若⊙O的半径为1，则BD的长为（）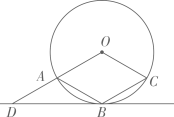

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
8. 已知反比例函数y＝ $- \frac{6}{x}$ ，下列说法中正确的是（）

A、图象分布在第一、三象限 B、点（﹣4，﹣3）在函数图象上 C、y随x的增大而增大 D、图象关于原点对称

查看试题解析
9. 已知Rt△ABC在平面直角坐标系中如图放置，∠ACB＝90°，且y轴是BC边的中垂线．已知S_△ABC＝6，反比例函数y＝ $\frac{k}{x}$ （k≠0）图象刚好经过A点，则k的值为（）

A、6 B、﹣6 C、3 D、﹣3

查看试题解析
10. 函数 $y = - \frac{k}{x}$ 与 $y = k x^{2} - k (k \neq 0)$ 在同一直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
11. 为防止疫情扩散，佩戴口罩成为疫情期间有效防范措施之一，某工厂为了能给市场提供充足的口罩，第一个月至第三个月生产口罩由67500袋增加到90000袋，设该工厂第一个月至第三个月生产口罩平均每月增长率为 $x$ ，则可列方程为（）

A、 $67500 (1 + 2 x) = 90000$ B、 $67500 {(1 + x)}^{2} = 90000$ C、 $67500 + 67500 (1 + x) + 67500 {(1 + x)}^{2} = 90000$ D、 $67500 \times 2 (1 + x) = 90000$

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c (a > 0)$ 过点(1，0)和点(0，－3)，且顶点在第三象限，设m＝a－b＋c，则m的取值范围是（）

A、－6＜m＜0 B、－6＜m＜－3 C、－3＜m＜0 D、－3＜m＜－1

查看试题解析

二、填空题

13. 若m是一元二次方程x²﹣3x+1＝0的一个根，则2020﹣m²+3m＝.

查看试题解析
14. 如图，六边形ABCDEF是半径为2的⊙O的内接正六边形，则劣弧CD的长为．

查看试题解析
15. 如图，飞镖游戏板中每一块小正方形除颜色外都相同．若某人向游戏板投掷飞镖一次，假设飞镖落在游戏板上，则飞镖落在阴影部分的概率是．

查看试题解析
16. 如图，已知⊙O的半径为3，弦AB、CD所对的圆心角分别是∠AOB、∠COD，若∠AOB与∠COD互补，弦CD＝4，则弦AB的长为．

查看试题解析
17. 如图，正三角形ABC的边长为2，点A ， B在半径为 $\sqrt{2}$ 的圆上，点C在圆内，将正三角形ABC绕点A逆时针旋转，当边AC第一次与圆相切时，旋转角为．

查看试题解析

三、解答题

18. 图①、图②、图③均是 $6 \times 6$ 的正方形网格，每个小正方形的顶点称为格点，小正方形边长为1，点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 、 $F$ 均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

(1)、在图①中以线段 $A B$ 为边画个中心对称四边形 $A B G H$ ．使其面积为9；

(2)、在图②中以线段 $C D$ 为边画一个轴对称四边形 $C D M N$ ．使其面积为10；

(3)、在图③中以线段 $E F$ 为边一个四边形 $E F P Q$ ，使其满足仅有一对对角都为直角．

查看试题解析
19. 解下列方程：

(1)、2（x﹣3）＝3x（3﹣x）；

(2)、3x²﹣5x＋2＝0

查看试题解析
20. 在甲口袋中有三个球分别标有数码1，-2，3；在乙口袋中也有三个球分别标有数码4，-5，6；已知口袋均不透明，六个球除标码不同外其他均相同，小明从甲口袋中任取一个球，并记下数码，小林从乙口袋中任取一个球，并记下数码.

(1)、用树状图或列表法表示所有可能的结果；

(2)、求所抽取的两个球数码的乘积为负数的概率.

查看试题解析
21. 如图，PA、PB是⊙O的切线，A、B为切点，∠P＝44°．

(1)、如图①，若点C为优弧AB上一点，求∠ACB的度数；

(2)、如图②，在（1）的条件下，若点D为劣弧AC上一点，求∠PAD＋∠C的度数．

查看试题解析
22. 在二次函数y＝ax²＋bx＋c（a≠0）中，函数y与自变量x的部分对应值如表：

x

…

0

1

2

3

4

…

y

…

3

0

﹣1

0

m

…

(1)、求这个二次函数的表达式及m的值；并利用所给的坐标网格，画出该函数图象；

(2)、将这个二次函数向左平移2个单位，再向上平移1个单位，求平移后的函数解析式．

查看试题解析

23. 某公司在市场销售“国耀2020”品牌手机，第一年售价定为4500元时，销售量为14百万台，根据以往市场调查经验，从第二年开始，手机每降低500元，销售量就增加2百万台，设该手机在市场销售的年份为x年（x为整数）．

(1)、根据题意，填写下表：

第x年	1	2	3	…	x
售价（元）	4500	4000		…
销售量（百万台）	14	16		…

(2)、设第x年“国耀2020”手机的年销售额为y（百万元），试问该公司销售“国耀2020”手机在第几年的年销售额可以达到最大？最大值为多少百万元？

(3)、若生产一台“国耀2020”手机的成本为3000元，如果你是该公司的决策者，要使公司的累计总利润最大，那么“国耀2020”手机销售年就应该停产，去创新新的手机．

查看试题解析

24. 如图1，已知△ABC中，∠ACB＝90°，AC＝BC＝6，点D在AB边的延长线上，且CD＝AB．

(1)、求BD的长度；

(2)、如图2，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'．
①若α＝30°，A'D'与CD相交于点E，求DE的长度；

②连接A'D、BD'，若旋转过程中A'D＝BD'时，求满足条件的α的度数．

(3)、如图3，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'，若点M为AC的中点，点N为线段A'D'上任意一点，直接写出旋转过程中线段MN长度的取值范围．

查看试题解析
25. 如图，抛物线y＝ $\frac{1}{2}$ x²﹣ $\frac{3}{2}$ x﹣2与x轴交于点A，点B，与y轴交于点C，直线y＝kx＋m，经过点B，C．

(1)、求k的值；

(2)、点P是直线BC下方抛物线上一动点，求四边形ACPB面积最大时点P的坐标；

(3)、若M是抛物线上一点，且∠MCB＝∠ABC，请直接写出点M的坐标．

查看试题解析