天津市和平区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列命题中，是真命题的是（）

A、直角三角形都相似 B、等腰三角形都相似 C、矩形都相似 D、正方形都相似

查看试题解析
3. 二次函数y＝ax²+bx+c图象上部分点的坐标如下表所示，则该函数图象的顶点坐标为（）

x

…

﹣1

0

1

2

…

y

…

0

3

4

3

…

A、（﹣1，0） B、（0，3） C、（1，4） D、（2，3）

查看试题解析
4. 如图，一个油桶靠在直立的墙边，量得 $W Y = 0.5 m$ ，并且 $X Y ⊥ W Y$ ，则这个油桶的底面半径是（）

A、 $0.25 m$ B、 $0.5 m$ C、 $0.75 m$ D、 $1m$

查看试题解析
5. 一个仅装有球的不透明布袋里共有4个球（只有编号不同），编号为1，2，3，5，从中任意摸出一个球，记下编号后放回，搅匀，再任意摸出一个球，则两次摸出的球的编号之和为偶数的概率是（）

A、 $\frac{5}{8}$ B、 $\frac{1}{2}$ C、 $\frac{5}{12}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图，Rt△ABC中，∠C＝90°，AB＝10，AC＝8，E是边AC上一点，AE＝5，ED⊥AB ，垂足为点D ，则AD的长是（）

A、16 B、 $\frac{25}{4}$ C、6 D、4

查看试题解析
7. 在如图所示的网格中，以点O为位似中心，四边形 $A B C D$ 的位似图形是（）

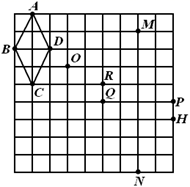A、四边形 $N P M Q$ B、四边形 $N P M R$ C、四边形 $N H M Q$ D、四边形 $N H M R$

查看试题解析
8. 如图，在▱OABC中，∠A＝60°，将▱OABC绕点O逆时针旋转得到▱OA′B'C′，且∠A'OC＝90°，设旋转角为α（0°＜α＜90°），则α的大小为（）

A、30° B、45° C、60° D、75°

查看试题解析
9. 设函数y＝a（x﹣h）²+k（a ， h ， k是实数，a≠0），当x＝1时，y＝1；当x＝8时，y＝8，（）

A、若h＝4，则a＜0 B、若h＝5，则a＞0 C、若h＝6，则a＜0 D、若h＝7，则a＞0

查看试题解析
10.
如图是抛物线形拱桥，当拱顶高离水面2m时，水面宽4m．水面下降2.5m，水面宽度增加（　　）

A、1m B、2m C、3m D、6m

查看试题解析
11. 如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上（不与点A，点C重合），BD与OA交于点E.设∠AED＝α，∠AOD＝β，则（）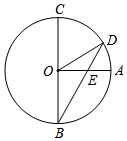

A、3α+β＝180° B、2α+β＝180° C、3α﹣β＝90° D、2α﹣β＝90°

查看试题解析
12. 如图，抛物线y＝ax²+bx+c的顶点坐标为（1，﹣4a），点A（4，y₁）是该抛物线上一点，若点B（x₂ ， y₂）是该抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②抛物线y＝ax²+bx+c与x轴交于点（﹣1，0），（3，0）；③若y₂＞y₁ ，则x₂＞4；④若0≤x₂≤4，则﹣3a≤y₂≤5a ．其中，正确结论的个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

13. 一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在岔路口随机选择一条路径，它获得食物的概率是．

查看试题解析
14. 已知正六边形的半径是3，则这个正六边形的边长是．

查看试题解析
15. 如图，在△ABC中，点D ， E在AC边上，且AE＝ED＝DC ．点F ， M在AB边上，且 $E F // D M // B C$ ，延长FD交BC的延长线于点N ，则 $\frac{E F}{B N}$ 的值＝．

查看试题解析
16. 已知圆锥的底面半径为40cm，母线长为90cm，则它的侧面展开图的圆心角为．

查看试题解析
17. 对于一个函数，自变量x取a时，函数值y也等于a ，我们称a为这个函数的不动点．如果二次函数y＝x²+2x+c有两个相异的不动点x₁ ， x₂ ，且x₁＜1＜x₂ ，则c的取值范围是．

查看试题解析
18. 已知正方形 $A B C D$ 的边长为6， $O$ 是 $B C$ 边的中点．

（Ⅰ）如图①，连接 $A O$ ，则 $A O$ 的长为．

（Ⅱ）如图②，点 $E$ 是正方形内一动点， $O E = 2$ ，连接 $D E$ ，将线段 $D E$ 绕点 $D$ 逆时针旋转90°得 $D F$ ．则线段 $O F$ 长的最小值为．

查看试题解析

三、解答题

19. 已知2是方程 $x^{2} - c = 0$ 的一个根，求常数 $c$ 的值及该方程的另一根．

查看试题解析
20. 已知， $⊙ O$ 中， $\overset{⌢}{A B} = \overset{⌢}{B C}$ ， $D$ 是 $⊙ O$ 上的点， $O C ⊥ B D$ ．

(1)、如图①，求证 $\overset{⌢}{A B} = \overset{⌢}{C D}$ ；

(2)、如图②，连接 $A B$ ， $B C$ ， $C D$ ， $D A$ ，若 $∠ A = 70 °$ ，求 $∠ B C D$ ， $∠ A D B$ 的大小．

查看试题解析
21. 已知⊙O的直径AB＝4，C为⊙O上一点，AC＝2．

(1)、如图①，点P是 $\overset{⌢}{B C}$ 上一点，求∠APC的大小；

(2)、如图②，过点C作⊙O的切线MC ，过点B作BD⊥MC于点D ， BD与⊙O交于点E ，求∠DCE的大小及CD的长．

查看试题解析
22. 一个直角三角形的两条直角边的和是 $7 cm$ ，面积是 $6 {cm}^{2}$ ，求两条直角边的长．

查看试题解析
23. 如图，已知矩形 $A B C D$ 的周长为 $36 cm$ ，矩形绕它的一条边 $C D$ 旋转形成一个圆柱．设矩形的一边 $A B$ 的长为 $x cm (x > 0)$ ，旋转形成的圆柱的侧面积为 $S {cm}^{2}$ ．

(1)、用含 $x$ 的式子表示：
矩形的另一边 $B C$ 的长为 $cm$ ；旋转形成的圆柱的底面圆的周长为 $cm$ ．

(2)、求 $S$ 关于 $x$ 的函数解析式及自变量 $x$ 的取值范围；

(3)、求当 $x$ 取何值时，矩形旋转形成的圆柱的侧面积最大；

(4)、若矩形旋转形成的圆柱的侧面积等于 $18 π {cm}^{2}$ ，则矩形的长是 $cm$ ，宽是 $cm$ ．

查看试题解析
24. 在△ABC中，∠ACB＝90°，CA＝CB＝2，点P是边AB的中点，连接CP．

(1)、如图①，∠B的大小＝（度），AB的长＝， CP的长＝；

(2)、延长BC至点O，使OC＝2BC，将△ABC绕点O逆时针旋转α（0°＜α＜180°）得到△A'B'C'，点A，B，C，P的对应点分别为A'，B'，C'，P'．
①图②，当α＝30°时，求点C′到直线OB的距离及点C'到直线AB的距离；

②当C′P'与△ABC的一条边平行时，求点P'到直线AC的距离（直接写出结果即可）．

查看试题解析
25. 如图，点A ， B ， C都在抛物线y＝ax²﹣2amx+am²+2m﹣5（其中﹣ $\frac{1}{4}$ ＜a＜0）上，AB∥x轴，∠ABC＝135°，且AB＝4．

(1)、当m＝1时，求抛物线的顶点坐标；

(2)、求点C到直线AB的距离（用含a的式子表示）；

(3)、若点C到直线AB的距离为1，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．

查看试题解析

x	…	﹣1	0	1	2	…
y	…	0	3	4	3	…