天津市滨海新区2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $4 x^{2} + 5 x = 81$ 化成一般形式后，它的二次项系数和常数项分别是（）

A、4，5 B、4，-5 C、4，81 D、4，081

查看试题解析
2. 2020年12月1日，《天津市生活垃圾管理条例》正式施行，标志着本市垃圾分类工作进入法制化、制度化、规范化阶段．生活垃圾分类实施“四分类”标准，即可回收物、厨余垃圾、有害垃圾、其他垃圾，分别对应下面四个图形，那么这些图形中为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列成语表示随机事件的是（）

A、缘木求鱼 B、水落石出 C、瓮中捉鳖 D、守株待兔

查看试题解析
4. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形， $A D$ 是 $⊙ O$ 的直径，若 $∠ C A D = 50 °$ ，则 $∠ A B C$ 的度数是（）

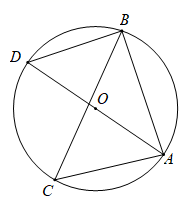A、30° B、40° C、50° D、60°

查看试题解析
5. 正方形ABCD内一点P，BP=2，把△ABP绕点B顺时针旋转90°得到△CBP′，则PP′的长为（）

A、2 $\sqrt{2}$ B、2 $\sqrt{3}$ C、3 D、3 $\sqrt{2}$

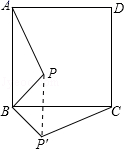查看试题解析
6. $△ A B C$ 与 $△ D E F$ 相似且对应高线之比为2：3，已知 $△ A B C$ 周长为40，则 $△ D E F$ 周长是（）

A、10 B、20 C、40 D、60

查看试题解析
7. 关于x的方程x（x﹣2）＝2x根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
8. 已知点 $(- 2 ， y_{1}) ， (- 1 ， y_{2}) ， (1 ， y_{3})$ 都在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，那么 $y_{1} ， y_{2}$ 与 $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
9. 将抛物线 $y = - 2 x^{2} - 3$ 向右平移2个单位长度，再向上平移1个单位长度，得到的抛物线解析式为（）

A、 $y = - 2 {(x + 2)}^{2} + 2$ B、 $y = - 2 {(x - 2)}^{2} - 2$ C、 $y = - 2 {(x + 2)}^{2} - 2$ D、 $y = - 2 {(x - 2)}^{2} - 5$

查看试题解析
10. 如图，正六边形ABCDEF内接于 $⊙ O$ ，过点O作 $O M ⊥$ 弦BC于点M ，若 $⊙ O$ 的半径为4，则弦心距OM的长为（）

A、 $2 \sqrt{3}$ B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
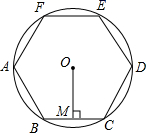11. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 40 °$ ，将 $△ A B C$ 绕点A逆时针方向旋转得 $△ A E F$ ，其中，E ， F是点B ， C旋转后的对应点，BE ， CF相交于点D ．当旋转到 $A F // B E$ 时， $∠ C A E$ 的大小是（）

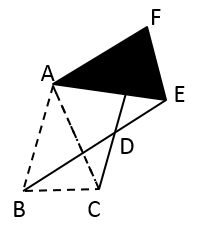A、90° B、75° C、60° D、45°

查看试题解析
12. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，则下列结论：① $a b c > 0$ ；②关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的根是-1，3；③ $a + 2 b = c$ ；④y最大值 $= \frac{4}{3} c$ ；其中正确的有（）个．

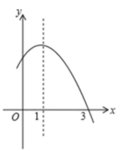A、4 B、3 C、2 D、1

查看试题解析

二、填空题

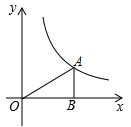
13. 二次函数 $y = x^{2} + 2 x + 3$ 的顶点坐标为．

查看试题解析
14. 一个不透明的袋子里装有6个只有颜色不同的球，其中4个红球，2个白球．从袋中任意摸出1个球，则摸出的球是红球的概率为．

查看试题解析
15. 如图，过反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上一点A作 $A B ⊥ x$ 轴于点B ，连接AO ，若 $S_{△ A O B} = 4$ ，则k的值为．

查看试题解析
16. 某区2019年投入教育经费2000万元，预计2021年投入教育经费2880万元．设这两年投入的教育经费的年平均增长率为 $x$ ，则可列方程为．

查看试题解析
17. 如图， $C D$ 是 $△ A B C$ 的边 $A B$ 上的中线，将线段 $A D$ 绕点 $D$ 顺时针旋转 $90 °$ 后，点 $A$ 的对应点 $E$ 恰好落在 $A C$ 边上，若 $A D = \sqrt{2}$ ， $B C = \sqrt{5}$ ，则 $A C$ 的长为．

查看试题解析

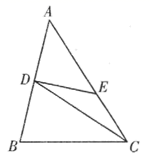
三、解答题

18. 如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段DE ，点A、B、D、E均在小正方形的顶点上．

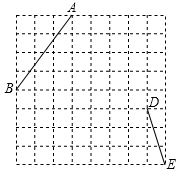(1)、①在方格纸中画出以AB为一边的锐角等腰三角形ABC ，点C在小正方形的顶点上，且 $△ A B C$ 的面积为10；
②在方格纸中画出以DE为一边的直角三角形DEF ，点F在小正方形的顶点上，且 $△ D E F$ 的面积为5；

(2)、连接CF ，则线段CF长为．

查看试题解析
19. 解方程： $x^{2} + 4 x + 8 = 2 x + 11$

查看试题解析
20. 如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（指针指在分界线时取指针右侧扇形的数）．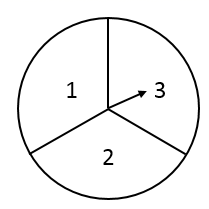

(1)、小王转动一次转盘指针指向3所在扇形的概率是．

(2)、请你用树状图或列表的方法求一次游戏结束后两数之和是5的概率．

查看试题解析
21. 如图，F为四边形ABCD边CD上一点，连接AF并延长交BC延长线于点E，已知 $∠ D = ∠ D C E$ ．

(1)、求证： $△ A D F ∽ △ E C F$ ；

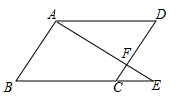(2)、若ABCD为平行四边形， $A B = 6$ ， $E F = 2 A F$ ，求FD的长度．

查看试题解析
22. 如图， $Δ A B C$ 和 $Δ E C D$ 都是等边三角形，直线 $A E$ ， $B D$ 交于点F.

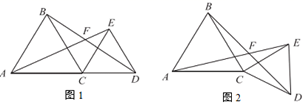(1)、如图1，当A，C，D三点在同一直线上时， $∠ A F B$ 的度数为，线段 $A E$ 与 $B D$ 的数量关系为.

(2)、如图2，当 $Δ E C D$ 绕点C顺时针旋转 $α$ $(0 ° \leq α < 360 °)$ 时，（1）中的结论是否还成立？若不成立，请说明理由：若成立，请就图2给予证明.

(3)、若 $A C = 4$ ， $C D = 3$ ，当 $Δ E C D$ 绕点C顺时针旋转一周时，请直接写出 $B D$ 长的取值范围.

查看试题解析
23. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + \frac{5}{2}$ 与 $x$ 轴交于 $A (5 ， 0)$ ， $B (- 1 ， 0)$ 两点，与y轴交于点C ．

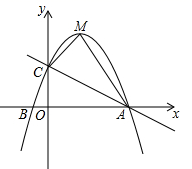(1)、求抛物线的解析式；

(2)、若点M是抛物线的顶点，连接AM ， CM ，求 $△ A M C$ 的面积；

(3)、若点Р是抛物线上的一个动点，过点Р作PE垂直y轴于点E ，交直线AC于点D ，过点D作x轴的垂线，垂足为点F ，连接EF ，当线段EF的长度最短时，求出点P的坐标．

查看试题解析
24. 如图，在平面直角坐标系中，已知抛物线 $y = a x^{2} + b x + \frac{5}{2}$ 与 $x$ 轴交于 $A (5 ， 0)$ ， $B (- 1 ， 0)$ 两点，与y轴交于点C ．

(1)、求抛物线的解析式；

(2)、若点M是抛物线的顶点，连接AM ， CM ，求 $△ A M C$ 的面积；

(3)、若点Р是抛物线上的一个动点，过点Р作PE垂直y轴于点E ，交直线AC于点D ，过点D作x轴的垂线，垂足为点F ，连接EF ，当线段EF的长度最短时，求出点P的坐标．

查看试题解析