河北省唐山市遵化市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O的位置关系是( )A、相离 B、相交 C、相切 D、不确定2. 对于每一象限内的双曲线 , 都随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、3. 圆锥的底面半径为1,母线长为3,则该圆锥侧面积为( )A、3 B、6π C、3π D、64. 如图,已知 为 上一点,若 ,则 的度数为( )
 A、50° B、80° C、100° D、130°5. 关于抛物线 的判断,下列说法正确的是( )A、抛物线的开口方向向上 B、抛物线的对称轴是直线 C、抛物线对称轴左侧部分是下降的 D、抛物线顶点到 轴的距离是26. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线7. 将函数y=x2的图象向左平移2个单位后,得到的新图象的解析式是( )A、 B、y= +4x+3 C、y= +4x+4 D、y= -4x+48. 已知关于 的二次三项式 的值恒为正,则 的取值范围是( )A、 B、 C、 D、9. 已知 , , 是1,3,4中的任意一个数( , , 互不相等),当方程 的解均为整数时,以1,3和此方程的所有解为边长能构成的多边形一定是( )A、轴对称图形 B、中心对称图形 C、轴对称图形或中心对称图形 D、非轴对称图形或中心对称图形10. 如图,在平面直角坐标系中,矩形 四个顶点的坐标 ,当双曲线 与矩形有四个交点时, 的取值范围是( )
A、50° B、80° C、100° D、130°5. 关于抛物线 的判断,下列说法正确的是( )A、抛物线的开口方向向上 B、抛物线的对称轴是直线 C、抛物线对称轴左侧部分是下降的 D、抛物线顶点到 轴的距离是26. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线7. 将函数y=x2的图象向左平移2个单位后,得到的新图象的解析式是( )A、 B、y= +4x+3 C、y= +4x+4 D、y= -4x+48. 已知关于 的二次三项式 的值恒为正,则 的取值范围是( )A、 B、 C、 D、9. 已知 , , 是1,3,4中的任意一个数( , , 互不相等),当方程 的解均为整数时,以1,3和此方程的所有解为边长能构成的多边形一定是( )A、轴对称图形 B、中心对称图形 C、轴对称图形或中心对称图形 D、非轴对称图形或中心对称图形10. 如图,在平面直角坐标系中,矩形 四个顶点的坐标 ,当双曲线 与矩形有四个交点时, 的取值范围是( ) A、 B、 C、 D、11. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠C=140°,则弧BD的长为( )
A、 B、 C、 D、11. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为3,∠C=140°,则弧BD的长为( ) A、 π B、 π C、π D、2π12. 图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )
A、 π B、 π C、π D、2π12. 图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )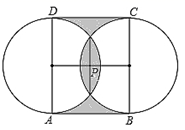 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 正比例函数 与反比例函数 交于 、 两点,若 点坐标是 ,则 点坐标是 .14. 已知扇形的半径为 ,弧长是 ,则此扇形的面积是 .15. 如果一个正n边形的每个内角为108°,那么这个正n边形的边数为 .
三、解答题

