河北省石家庄市辛集市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 用长为1cm,2cm,3cm的三条线段围成三角形的事件是( )
A、随机事件 B、必然事件 C、不可能事件 D、以上说法都不对2. 若函数 是反比例函数,且它的图象在第一、三象限,则m的值为( )A、2 B、﹣2 C、 D、3. 如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )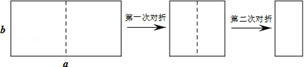 A、a= b B、a=2b C、a=2 b D、a=4b4. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( )
A、a= b B、a=2b C、a=2 b D、a=4b4. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC与△ADE相似的是( ) A、∠C=∠AED B、∠B=∠D C、 D、5. 如图,四边形 内接于 , ,若 ,则 的度数为( )
A、∠C=∠AED B、∠B=∠D C、 D、5. 如图,四边形 内接于 , ,若 ,则 的度数为( ) A、 B、 C、 D、6. 一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是 ( )A、6π B、4π C、8π D、47. 在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )A、11 B、13 C、24 D、308. 已知关于 的方程 没有实数解,则函数 的图象大致是图中的( )A、
A、 B、 C、 D、6. 一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个圆,那么这个几何体的表面积是 ( )A、6π B、4π C、8π D、47. 在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )A、11 B、13 C、24 D、308. 已知关于 的方程 没有实数解,则函数 的图象大致是图中的( )A、 B、
B、 C、
C、 D、
D、 9. 已知 , , 在二次函数 的图象上,则 , , 的大小关系正确的是A、 B、 C、 D、10. 2020年,新型冠状病毒感染的肺炎疫情牵动着全国人民的心.某学生写了一份预防新型冠状病毒倡议书在微信朋友圈传播,规则为:将倡议书发表在自己的朋友圈,再邀请 个好友转发倡议书,每个好友转发倡议书,又邀请 个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有931人参与了传播活动,则方程列为( )A、 B、 C、 D、11. 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,若⊙O的直径为4,则弦AB长为( )
9. 已知 , , 在二次函数 的图象上,则 , , 的大小关系正确的是A、 B、 C、 D、10. 2020年,新型冠状病毒感染的肺炎疫情牵动着全国人民的心.某学生写了一份预防新型冠状病毒倡议书在微信朋友圈传播,规则为:将倡议书发表在自己的朋友圈,再邀请 个好友转发倡议书,每个好友转发倡议书,又邀请 个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有931人参与了传播活动,则方程列为( )A、 B、 C、 D、11. 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A,B两点,若⊙O的直径为4,则弦AB长为( )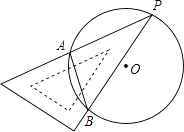 A、2 B、3 C、 D、12. 已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )A、 B、 C、 D、213. 如图,从渔船 处测得灯塔 在北偏东55°方向上,这艘渔船以 的速度向正东方向航行,半小时后到达 处,在 处测得灯塔 在北偏东20°方向上,此时灯塔 与渔船的距离( )
A、2 B、3 C、 D、12. 已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )A、 B、 C、 D、213. 如图,从渔船 处测得灯塔 在北偏东55°方向上,这艘渔船以 的速度向正东方向航行,半小时后到达 处,在 处测得灯塔 在北偏东20°方向上,此时灯塔 与渔船的距离( ) A、 B、 C、 D、14. 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm、1cm, 若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为( )cm
A、 B、 C、 D、14. 如图,已知正方形ABCD与正方形AEFG的边长分别为4cm、1cm, 若将正方形AEFG绕点A旋转,则在旋转过程中,点C、F之间的最小距离为( )cm A、3 B、2 C、4 -1 D、315. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )
A、3 B、2 C、4 -1 D、315. 如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y= (x>0)的图象上,则经过点B的反比例函数解析式为( )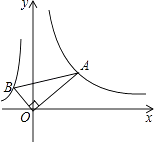 A、y=﹣ B、y=﹣ C、y=﹣ D、y=16. 我们定义一种新函数:形如 (a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:其中正确结论的个数是( )
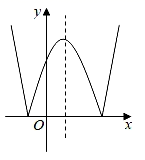
A、y=﹣ B、y=﹣ C、y=﹣ D、y=16. 我们定义一种新函数:形如 (a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:其中正确结论的个数是( )①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4,
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
17. 如果关于 的一元二次方程 的一个解是 ,则 .18. 如图,在反比例函数 ( )的图象上,有点 、 、 、 ,它们的横坐标依次为2,4,6,8……分别过这些点作 轴与 轴的垂线,图中所构成的阴影部分的面积从左到右依次为 、 、 …,则点 的坐标为 , 阴影部分的面积和 为 .
 19. 曲线 在直角坐标系中的位置如图所示,曲线 是由半径为2,圆心角为 的 ( 是坐标原点,点 在 轴上)绕点 旋转 ,得到 ;再将 绕点 旋转 ,得到 ;……依次类推,形成曲线 ,现有一点 从 点出发,以每秒 个单位长度的速度,沿曲线 向右运动,则点 的坐标为;在第 时,点 的坐标为 .
19. 曲线 在直角坐标系中的位置如图所示,曲线 是由半径为2,圆心角为 的 ( 是坐标原点,点 在 轴上)绕点 旋转 ,得到 ;再将 绕点 旋转 ,得到 ;……依次类推,形成曲线 ,现有一点 从 点出发,以每秒 个单位长度的速度,沿曲线 向右运动,则点 的坐标为;在第 时,点 的坐标为 .
三、解答题
-
20. 解方程:(1)、 ;(2)、 .21. 某商场销售一批衬衫,每件成本为50元,如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件,如果商场销售这批衬衫要获利润12000元,又使顾客获得更多的优惠,那么这种衬衫售价应定为多少元?(1)、设提价了 元,则这种衬衫的售价为元,销售量为件.(2)、列方程完成本题的解答.22. 如图,已知一次函数 的图像与反比例函数 的图像交于点 和点 ,与 轴交于点 .
 (1)、反比例函数的表达式;一次函数的表达式.(2)、若在 轴上有一点 ,其横坐标是1,连接 ,求 的面积.23. “五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.(1)、请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;(2)、判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.24. 探究:某学校数学社团遇到这样一个题目:如图①,在 中,点 在线段 上, , , , ,求 的长.
(1)、反比例函数的表达式;一次函数的表达式.(2)、若在 轴上有一点 ,其横坐标是1,连接 ,求 的面积.23. “五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.(1)、请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;(2)、判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.24. 探究:某学校数学社团遇到这样一个题目:如图①,在 中,点 在线段 上, , , , ,求 的长.
经过社团成员讨论发现,过点 作 ,交 的延长线于点 ,连结 ,如图②所示,通过构造 就可以解决问题.
(1)、请你写出求 长的过程.(2)、应用:如图③,在四边形 中,对角线 与 相交于点 , , , .若 ,请你求出 的长.25. 如图,抛物线 : 与抛物线 : 开口大小相同、方向相反,它们相交于 , 两点,且分别与 轴的正半轴交于点 ,点 , .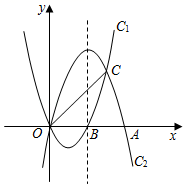 (1)、求抛物线 的解析式;(2)、在抛物线 的对称轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由;(3)、 是直线 上方抛物线 上的一个动点,连接 , , 运动到什么位置时, 面积最大?并求出最大面积.26. 如图,在 中, , , ,半径为2的 从点 开始(如图1)沿直线 向右滚动,滚动时始终与直线 相切(切点为 ),当 与 只有一个公共点时滚动停止,作 于点 .
(1)、求抛物线 的解析式;(2)、在抛物线 的对称轴上是否存在点 ,使 的值最小?若存在,求出点 的坐标,若不存在,说明理由;(3)、 是直线 上方抛物线 上的一个动点,连接 , , 运动到什么位置时, 面积最大?并求出最大面积.26. 如图,在 中, , , ,半径为2的 从点 开始(如图1)沿直线 向右滚动,滚动时始终与直线 相切(切点为 ),当 与 只有一个公共点时滚动停止,作 于点 . (1)、图1中, 在 边上截得的弦长 ;(2)、当圆心落在 上时,如图2,判断 与 的位置关系,并说明理由.(3)、在 滚动过程中,线段 的长度随之变化,设 , ,求出 与 的函数关系式,并直接写出 的取值范围.
(1)、图1中, 在 边上截得的弦长 ;(2)、当圆心落在 上时,如图2,判断 与 的位置关系,并说明理由.(3)、在 滚动过程中,线段 的长度随之变化,设 , ,求出 与 的函数关系式,并直接写出 的取值范围.