河北省石家庄市高邑县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 一元二次方程 的解为( )A、 B、 C、 D、2. 从一组数据1,2,2,3中任意取走一个数,剩下三个数不变的是( )A、平均数 B、众数 C、中位数 D、方差3. 已知函数 是反比例函数,则此反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限4. 若抛物线y=kx2﹣2x﹣1与x轴有两个不同的交点,则k的取值范围为( )A、k>﹣1 B、k≥﹣1 C、k>﹣1且k≠0 D、k≥﹣1且k≠05. 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是( )
 A、① B、② C、③ D、④6. 如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段 AC 的长为( )
A、① B、② C、③ D、④6. 如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC,则线段 AC 的长为( )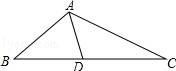 A、4 B、4 C、6 D、47. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )
A、4 B、4 C、6 D、47. 如图, 分别与 相切于 点,C为 上一点, ,则 ( )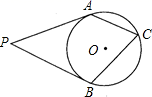 A、 B、 C、 D、8. 一个扇形半径30cm,圆心角120°,用它作一个圆锥的侧面,则圆锥底面半径为( )A、5cm B、10cm C、20cm D、30cm9. 在反比例函数y= 的图象上有两点A(x1 , y1)、B(x2 , y2).若x1<0<x2 , y1<y2则k的取值范围是( )A、k≥ B、k> C、k<﹣ D、k<10. 老师设计了接力游戏,用合作的方式完成“求抛物线 的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
A、 B、 C、 D、8. 一个扇形半径30cm,圆心角120°,用它作一个圆锥的侧面,则圆锥底面半径为( )A、5cm B、10cm C、20cm D、30cm9. 在反比例函数y= 的图象上有两点A(x1 , y1)、B(x2 , y2).若x1<0<x2 , y1<y2则k的取值范围是( )A、k≥ B、k> C、k<﹣ D、k<10. 老师设计了接力游戏,用合作的方式完成“求抛物线 的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是( )
A、只有丁 B、乙和丁 C、乙和丙 D、甲和丁11. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、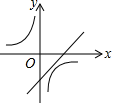 B、
B、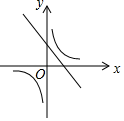 C、
C、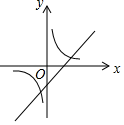 D、
D、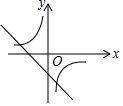 12. 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC, ,△CEF的面积为2,则△EBC的面积为( )
12. 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC, ,△CEF的面积为2,则△EBC的面积为( ) A、4 B、6 C、8 D、1213. 如图, 的外切正六边形 的边长为2,则图中阴影部分的面积为( )
A、4 B、6 C、8 D、1213. 如图, 的外切正六边形 的边长为2,则图中阴影部分的面积为( ) A、 B、 C、 D、14. 如图钓鱼竿AC长6m , 露在水面上的鱼线BC长3 m , 钓者想看看鱼钓上的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A、 B、 C、 D、14. 如图钓鱼竿AC长6m , 露在水面上的鱼线BC长3 m , 钓者想看看鱼钓上的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( ) A、3m B、 m C、 m D、4m15. 服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )A、150元 B、160元 C、170元 D、180元16. 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
A、3m B、 m C、 m D、4m15. 服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )A、150元 B、160元 C、170元 D、180元16. 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )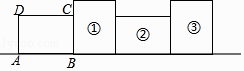 A、2017π B、2034π C、3024π D、3026π
A、2017π B、2034π C、3024π D、3026π二、填空题
-
17. 在Rt△ABC中,∠C=90°,AC=9,sinB= ,则BC=.18. 如图, 在中, ,I是内心,O是外心,则 .
 19. 如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上 ,则k值为 .
19. 如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上 ,则k值为 . 20. 如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(- ,y1),( ,y2)是抛物线上两点,则y1<y2 , 其中结论正确的是 .
20. 如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(- ,y1),( ,y2)是抛物线上两点,则y1<y2 , 其中结论正确的是 .
三、解答题
-
21. 已知关于x的方程 =0.
(1)、求证:不论a取何实数,该方程都有两个不相等的实数根。(2)、当a=1时,求该方程的根。22. 如图是某货站传送货物的平面示意图为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角使其由 改为 ,已知原传送带 长为4米.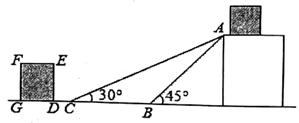 (1)、求新传送带 的长度;(结果保留根号)(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离 点5米的货物 是否需要挪走,并说明理由(结果精确到0.1米参考数据: , , )23. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)、求新传送带 的长度;(结果保留根号)(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离 点5米的货物 是否需要挪走,并说明理由(结果精确到0.1米参考数据: , , )23. “垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题: (1)、接受问卷调查的学生共有人,条形统计图中 的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.24. 如图,直线 与双曲线 在第一象限内交于A、B两点,已知 , .
(1)、接受问卷调查的学生共有人,条形统计图中 的值为;(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为;(3)、若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.24. 如图,直线 与双曲线 在第一象限内交于A、B两点,已知 , .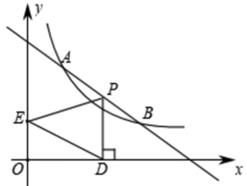 (1)、求 的值及直线 的解析式.(2)、根据函数图象,直接写出不等式 的解集.(3)、设点P是线段 上的一个动点,过点P作 轴于点D,E是y轴上一点,当 的面积最大时,请求出此时P点的坐标.
(1)、求 的值及直线 的解析式.(2)、根据函数图象,直接写出不等式 的解集.(3)、设点P是线段 上的一个动点,过点P作 轴于点D,E是y轴上一点,当 的面积最大时,请求出此时P点的坐标.

