河北省秦皇岛市青龙县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、52. 下列方程中,是一元二次方程的为( )A、 B、 C、 D、3. 在Rt△ABC中,∠C=90°,AC=4,BC=3,则cosB的值为( )A、 B、 C、 D、4. 抛物线y=3(x-2)2+1的顶点坐标是( )A、(2,1) B、(-2,1) C、(-2,-1) D、(1,2)5. 老师对甲、乙两人的五次数学测验成绩进行统计,得出两人五次测验成绩的平均分均为90分,方差分别是S2甲=51、S2乙=12,由此可知( )A、甲比乙的成绩稳定 B、乙比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定6. 若方程 的两个实数根分别为 、 ,则 等于( )A、3 B、 C、-3 D、7. 为了了解某校3000名学生的体重情况,从中抽取了200名学生的体重,就这个问题来说,下列说法正确的是( )A、3000名学生是总体 B、3000名学生的体重是总体 C、每个学生是个体 D、200名学生是所抽取的一个样本8. 如图,△ABC∽△ADE , 则下列比例式正确的是( )
 A、 B、 C、 D、9. 函数 的图象位于( ).A、第三象限 B、第一、三象限 C、第二、四象限 D、第二象限10. 某厂今年3月份的产值为5万元;5月份上升到7万元,这两个月的平均每月增长的百分率是多少?若设平均每月增长的百分率为 ,则列出的方程是( )A、 B、 C、 D、11. 如图,反比例函数y=
A、 B、 C、 D、9. 函数 的图象位于( ).A、第三象限 B、第一、三象限 C、第二、四象限 D、第二象限10. 某厂今年3月份的产值为5万元;5月份上升到7万元,这两个月的平均每月增长的百分率是多少?若设平均每月增长的百分率为 ,则列出的方程是( )A、 B、 C、 D、11. 如图,反比例函数y= (k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( ) A、
(k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是( ) A、 B、
B、 C、
C、 D、
D、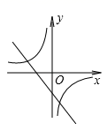 12. 如图,在平行四边形 中,点 是边 上一点,且 , 交对角线 于点 ,则 与 的周长比为( )
12. 如图,在平行四边形 中,点 是边 上一点,且 , 交对角线 于点 ,则 与 的周长比为( ) A、9 B、3 C、 D、213. 在一次比赛前,教练预言说:“这场比赛我们队有60%的机会获胜”,则下列说法中与“有60%的机会获胜”的意思接近的是( )A、他这个队赢的可能性较大 B、若这两个队打10场,他这个队会赢6场 C、若这两个队打100场,他这个队会赢60场 D、他这个队必赢14. 如图, 是正六边形ABCDEF的外接圆,P为 上除C,D外的任意一点,则 的值为( )
A、9 B、3 C、 D、213. 在一次比赛前,教练预言说:“这场比赛我们队有60%的机会获胜”,则下列说法中与“有60%的机会获胜”的意思接近的是( )A、他这个队赢的可能性较大 B、若这两个队打10场,他这个队会赢6场 C、若这两个队打100场,他这个队会赢60场 D、他这个队必赢14. 如图, 是正六边形ABCDEF的外接圆,P为 上除C,D外的任意一点,则 的值为( ) A、 B、1 C、 D、15. 二次函数 的图象如图所示,则函数值 时,x的取值范围是( )
A、 B、1 C、 D、15. 二次函数 的图象如图所示,则函数值 时,x的取值范围是( ) A、 B、 C、 D、 或16. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )
A、 B、 C、 D、 或16. 有一题目:“已知;点 为 的外心, ,求 .”嘉嘉的解答为:画 以及它的外接圆 ,连接 , ,如图.由 ,得 .而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )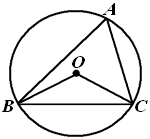 A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值
A、淇淇说的对,且 的另一个值是115° B、淇淇说的不对, 就得65° C、嘉嘉求的结果不对, 应得50° D、两人都不对, 应有3个不同值二、填空题
-
17. 数据2,3,5,5,4的众数是 .18. 已知 是一元二次方程 的一个解,则m的值是 .19. 如图, 中, // , , , ,则 的长为
 20. “经过某交通信号灯的路口,遇到红灯”是事件(填“必然”、“不可能“、“随机”)21. 点 在反比例函数 的图象上,则k的值为22. 如图,∠1=∠2,添加一个条件使得△ADE∽△ACB .
20. “经过某交通信号灯的路口,遇到红灯”是事件(填“必然”、“不可能“、“随机”)21. 点 在反比例函数 的图象上,则k的值为22. 如图,∠1=∠2,添加一个条件使得△ADE∽△ACB . 23. 已知 ,则 的值为.24. 在一个不透明的袋中装着3个红球和1个黄球,它们除颜色外其余都相同,随机从袋中摸出1个球,恰好是红球的概率为25. 将抛物线 向下平移3个单位,再向左平移2个单位,则平移后的抛物线表达式为26. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为mm.
23. 已知 ,则 的值为.24. 在一个不透明的袋中装着3个红球和1个黄球,它们除颜色外其余都相同,随机从袋中摸出1个球,恰好是红球的概率为25. 将抛物线 向下平移3个单位,再向左平移2个单位,则平移后的抛物线表达式为26. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为mm.
三、解答题
-
27.(1)、用适当的方法解方程:3(x-1)2=2(x-1)(2)、计算:28. 扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手.为了解同学们“智慧学堂”平台使用的熟练程度,某校随机抽取了部分同学进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.

根据以上信息,回答下列问题:
(1)、本次调查的样本容量是 , 扇形统计图中表示A等级的扇形圆心角为 ;(2)、补全条形统计图;(3)、学校拟对“不太熟练或不熟练”的同学进行平台使用的培训,若该校有2000名学生,试估计该校需要培训的学生人数.29. 小明家所在居民楼的对面有一座大厦AB,AB= 米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
(参考数据: )
30. 某产品的成本是120元/件,在试销阶段,当产品的售价为x(元/件)时,日销售量为(200-x)件.(1)、写出用售价x(元/件)表示每日的销售利润y(元)的表达式(2)、当日销售利润是1500元时,产品的售价是多少?日销售量是多少件?(3)、当售价定位多少时,日销售利润最大?最大日销售利润是多少元?31. 如图,在平面直角坐标系 中,反比例函数 的图像经过点 ,点 在 轴的负半轴上, 交 轴于点 , 为线段 的中点.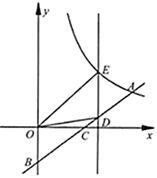 (1)、 , 点 的坐标为;(2)、若点 为线段 上的一个动点,过点 作 轴,交反比例函数图象于点 ,求 面积的最大值.32. 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2
(1)、 , 点 的坐标为;(2)、若点 为线段 上的一个动点,过点 作 轴,交反比例函数图象于点 ,求 面积的最大值.32. 如图,在矩形ABCD中,AB=6cm,BC=8cm,动点P以2cm/s的速度从点A出发,沿AC向点C移动,同时动点Q以1cm/s的速度从点C出发.沿CB向点B移动,设P、Q两点移动ts(0<t<5)后,△CQP的面积为Scm2 (1)、在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;(2)、当运动时间为多少秒时,△CPQ与△CAB相似.
(1)、在P、Q两点移动的过程中,△CQP的面积能否等于3.6cm2?若能,求出此时t的值;若不能,请说明理由;(2)、当运动时间为多少秒时,△CPQ与△CAB相似.