河北省承德市宽城县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-10-09 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在Rt△ABC中，∠C=90，AC=3，BC=4，则斜坡AB的坡度为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{5}{3}$

查看试题解析
2. 如果一个三角形的面积为10，底边长为x ，底边上的高为y ，则y与x 的函数表达式为（）

A、y= $\frac{10}{x}$ B、y= $\frac{5}{x}$ C、y= $\frac{20}{x}$ D、y= $\frac{x}{20}$

查看试题解析
3. 方程 $(m - 2) x^{m^{2} + m - 4} - m x + 5 = 0$ 是关于x的一元二次方程，则m的值为（）

A、﹣3 B、2 C、3 D、2或﹣3

查看试题解析
4. 二次函数 $y = - x^{2} + 4 x + 1$ 有（）

A、最大值5 B、最小值5 C、最大值-3 D、最小值-3

查看试题解析
5. 一次演讲比赛中，评委将从演讲内容、演讲能力，演讲效果三方面为选手打分，并按如图所示的权重计入总评成绩，小明的三项成绩分别是90，95，90（单位：分），则他的总评成绩是（）

A、91分 B、91.5分 C、92分 D、92.5分

查看试题解析
6. 图中的两个三角形是位似图形，它们的位似中心是（）

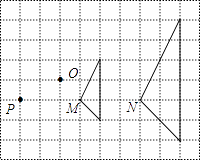A、点P B、点O C、点M D、点N

查看试题解析
7. 反比例函数y= $\frac{k}{x}$ 的图像如图所示，下列说法正确的是（）

A、k>0 B、y 随x的增大而增大 C、若矩形 OABC的面积为2，则 $k = - 2$ D、若图像上点B的坐标是（-2，1），则当x<-2时，y的取值范围是y<1

查看试题解析
8. 如图．PA ， PB是⊙O的两条切线，切点分别为A ， B ，连接OA ， OB ， OP ， AB ．若 OA=1，∠APB=60°，则△PAB 的周长为（）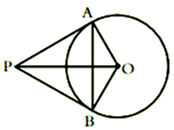

A、2 $\sqrt{3}$ B、4 C、3 $\sqrt{3}$ D、2 $\sqrt{3}$ +2

查看试题解析
9. 如图，在Rt△ABC中，∠CAB=90，AD⊥BC于点D，若BD=2，sinC= $\frac{\sqrt{5}}{5}$ ，则线段 AB 的长为（）

A、10 B、4 C、4 $\sqrt{5}$ D、2 $\sqrt{5}$

查看试题解析
10. 一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了1.4m，则此时排水管水面宽为（）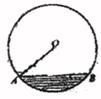

A、1.2m B、1.4m C、1.6m D、1.8m

查看试题解析
11. 如图，在 $Δ A B C$ 中，点 $D$ 在 $A B$ 上， $∠ A C D = ∠ B$ ．若 $A D = 2 ， B D = 3$ ，则 $A C$ 等于（）

A、5 B、6 C、 $\sqrt{6}$ D、 $\sqrt{10}$

查看试题解析
12. 如图，在边长为1的正六边形 $A B C D E F$ 中，M是边 $D E$ 上一点，则线段 $A M$ 的长可以是（）

A、1.4 B、1.6 C、1.8 D、2.2

查看试题解析
13. 已知函数 $y = {\begin{array}{l} x^{2} + 1 (x \geq - 1) \\ \frac{2}{x} (x < - 1) \end{array}$ 则下列图像正确的是（）

A、 B、 C、 D、

查看试题解析
14. 如图1，有一张长 $32 cm$ ，宽 $16 cm$ 的长方形硬纸片，裁去角上2个小正方形和2个小长方形（图中阴影部分）之后，恰好折成如图2所示的有盖纸盒.若纸盒的底面积是 $130 {cm}^{2}$ ，则纸盒的高为（）

A、 $2 cm$ B、 $2.5 cm$ C、 $3 cm$ D、 $4 cm$

查看试题解析
15. 点P(m，n)在以y轴为对称轴的二次函数y＝x²+ax+4的图象上.则m﹣n的最大值等于（）

A、 $\frac{15}{4}$ B、4 C、﹣ $\frac{15}{4}$ D、﹣ $\frac{17}{4}$

查看试题解析
16. 在边长为1的正方形铁皮上剪下一个扇形（率径为R）和一个圆形（率径为r），使之恰好围成一个圆锥．嘉嘉说图1剪下的圆和扇形一定不可以围成一个圆锥，淇淇说图中剪下的圆和扇形有可能围成一个圆锥，还需要满足条件R=4r，则（）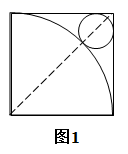

A、只有嘉嘉的说法正确 B、只有淇淇的说法正确 C、两个人的说法均正确 D、两人的说法均不正确

查看试题解析

二、填空题

17. 已知三条线段的长分别为2，x ， 4，若2是x和4的比例中项，则x= ．

查看试题解析
18. 若关于 $x$ 的二次函数 $y = - x^{2} + 2 x + m - 3$ 的函数值恒为负数，则 $m$ 的取值范围为．

查看试题解析
19. 如图，在平面直角坐标系 $x o y$ 中，直线 y=mx+1与双曲线 y= $\frac{k}{x}$ （k>0）相交于点A，B，已知点B（a，-2），点C在×轴正半轴上，点D（2，-3），连接 OA，OD，DC，AC，四边形AODC为菱形．

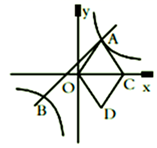(1)、反比例函数的表达式为；

(2)、不等式 $\frac{k}{x}$ >mx+1 的解集是；

(3)、设P是y轴上一动点，且△OAP的面积等于菱形OACD的面积，则点P的坐标为．

查看试题解析

三、解答题

20. 计算下列各小题

(1)、 $2 c o s^{2} 45 ° + t a n 60 ° \cdot t a n 30 ° - c o s 60 °$ ；

(2)、 $3 \tan 30 ° + \sqrt{8} \cos 45 ° + \sqrt{{(1 - \tan 60 °)}^{2}}$ ．

查看试题解析
21. 定义：若两个一元二次方程有且只有一个相同的实数根，我们就称这两个方程为“同伴方程”．例如x²=4和（x-2）（x+3）=0有且只有一个相同的实数根x=2，所以这两个方程为“同伴方程”．

(1)、根据所学定义，下列方程属于“同伴方程”的是；（只填写序号即可）
① ${(x - 1)}^{2} = 9$ ； ② $x^{2} + 4 x + 4 = 0$ ； ③ $(x + 4) (x - 2) = 0$ ；

(2)、若关于x的一元二次方程x²-2x=0与x²+3x+m-1=0为“同伴方程”，求m的值．

查看试题解析

22. 为宣传普及新冠肺炎防控知识，引导学生做好防控，某校举行了主题为“防控新冠，从我做起”的线上知识竞赛活动，测试内容为 20道判断题，每道题5分，满分 100分．为了解八、九年级学生此次竞赛成绩的情况，分别随机在八、九年级各抽取了20名参赛学生的成绩，已知抽取得到的八年级的数据如下（单位：分）：80，95，75，75，90，75，80，65， 80.85.75，65，70，65，85，70，95，80，75.80．为了便于分析数据，统计员对八年级数据进行了整理，得到表1

表1：

等级	分数（单位：分）	学生数
D	60＜x≤70	5
C	70＜x≤80	a
B	80＜x≤90	b
A	90＜x≤100	2

表2：

年级	平均分	中位数	优秀率
八年级	78分	c分	m%
九年级	76分	82.5分	50%

[八、九年级成绩的平均数、中位数、优秀率如表2所示（分数80分以上，不含80分为优秀）．]

(1)、根据题目信息填空：a= ，c= ， m=；

(2)、八年级王宇和九年级程义的分数都为80分，请判断王字、程义在各自年级的排名哪位更靠前?请筒速你的理由．

查看试题解析

23. 如图，在阳光下，小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米，同时小强同学在测量树的高度时，发现树的影子有一部分（0.2 米）落在教学楼的第一级台阶上，落在地面上的影长为4.42米，每级台阶高为0.3米．小玲说：“要是没有台阶遮挡的话，树的影子长度应该是 4.62米．”小强说：“要是没有台阶遮挡的话，树的影子长度肯定比 4.62米要长．”

(1)、你认为谁的说法对?并说明理由；

(2)、请根据小玲和小强的测量数据计算树的高度．

查看试题解析
24. 为满足市场需求，某超市购进一种品牌糕点，每盒进价是40元．超市规定每盒售价不得少于45元．根据以往销售经验发现，当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高 $1$ 元，每天要少卖出20盒．

(1)、试求出每天的销售量 $y$ （盒）与每盒售价 $x$ （元）之间的函数关系式；

(2)、当每盒售价定为多少元时，每天销售的利润 $P$ （元）最大？最大利润是多少？

(3)、如果超市想要每天获得不低于 $6000$ 元的利润，那么超市每天至少销售糕点多少盒？

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，D为AB边上的一点，以AD为直径的⊙O交BC于点E ，过点C作CG⊥AB交AB于点G ，交AE于点F ，过点E作EP⊥AB交AB于点P ， ∠EAD＝∠DEB ．

(1)、求证：BC是⊙O的切线；

(2)、求证：CE＝EP；

(3)、若CG＝12，AC＝15，求四边形CFPE的面积．

查看试题解析
26. 如图，二次函数y=- $\frac{1}{2}$ x²+2x+1的图像与一次函数y=-x+1的图像交于A、B两点，点C是二次函数图象的顶点，P是x轴下方线段AB上一点（与端点不重合），过点P分别作x轴的垂线和平行线，垂足为E，平行线交直线BC于点F．

(1)、若反比例函数 y= $\frac{k}{x}$ 的图像正好过点 C，求k的值；

(2)、求当 $△ P E F$ 面积最大时，点 P的坐标；

(3)、如图2，将二次函数y=- $\frac{1}{2}$ x²+2x+1关于x轴对称得到新抛物线 $y^{'}$ ， $y^{'}$ 的顶点为 $C^{'}$ ，再将 $y^{'}$ 沿直线 AB的方向平移得到新抛物线 $y^{″}$ ， $y^{″}$ 的顶点为 $C^{″}$ ．在 $y^{″}$ 平移过程中，是否存在一个合适的位置，使得 $△ A B C^{″}$ 是一个直角三角形?若存在，请直接写出所有满足条件的点 $C^{″}$ 的坐标；若不存在，请说明理由．

查看试题解析