河北省承德市丰宁满族自治县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是确定性事件的是( )A、篮球队员在罚球线上投篮一次,未投中 B、经过有交通信号灯的路口,遇到绿灯 C、投掷一枚骰子(六个面分别刻有 到 的点数),向上一面的点数大于 D、任意画一个三角形,其外角和是3. 方程(x﹣1)(x﹣2)=0的解是( )A、1 B、2 C、1和2 D、﹣1和﹣24. 抛物线 的顶点坐标为( )A、(−2,1) B、(2,−1) C、(1,2) D、(2,1)5. 将点 绕原点顺时针旋转 得到的点的坐标是( )A、 B、 C、 D、6. 下列方程中,无实数根的方程是( )A、 B、 C、 D、7. 正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 ( )A、 B、 C、 D、8. 如图,⊙O的弦AB=8,M是弦AB上的动点,若OM的最小值是3,则⊙O的半径是( )
2. 下列事件中,是确定性事件的是( )A、篮球队员在罚球线上投篮一次,未投中 B、经过有交通信号灯的路口,遇到绿灯 C、投掷一枚骰子(六个面分别刻有 到 的点数),向上一面的点数大于 D、任意画一个三角形,其外角和是3. 方程(x﹣1)(x﹣2)=0的解是( )A、1 B、2 C、1和2 D、﹣1和﹣24. 抛物线 的顶点坐标为( )A、(−2,1) B、(2,−1) C、(1,2) D、(2,1)5. 将点 绕原点顺时针旋转 得到的点的坐标是( )A、 B、 C、 D、6. 下列方程中,无实数根的方程是( )A、 B、 C、 D、7. 正方体的棱长为x,表面积为y,则y与x之间的函数关系式为 ( )A、 B、 C、 D、8. 如图,⊙O的弦AB=8,M是弦AB上的动点,若OM的最小值是3,则⊙O的半径是( )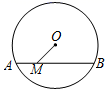 A、4 B、5 C、6 D、79. 如图,如果将正方形甲旋转到正方形乙的位置,可以作为旋转中心的点有( )
A、4 B、5 C、6 D、79. 如图,如果将正方形甲旋转到正方形乙的位置,可以作为旋转中心的点有( )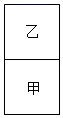 A、1个 B、2个 C、3个 D、4个10. 某口罩生产厂2020年1月份平均日产20万个,1月底因防控新冠疫情需求,工厂立即决定从2月份起扩大产能,3月份平均日产量达到45万个,则口罩日产量的月平均增长率是( )A、20% B、30% C、40% D、50%11. 已知二次函数 ,下列叙述中正确的是( )A、图象的开口向上 B、图象的对称轴为直线 C、函数有最小值 D、当 时,函数值 随自变量 的增大而减小12. 若⊙O的内接正n边形的边长与⊙O的半径相等,则 ( )A、6 B、 C、 D、413. 若关于 的一元二次方程 的常数项为 ,则 的值等于( )A、2 B、−2 C、±2 D、−414. 若点 , , 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、15. 如图,在扇形AOB中,∠AOB=90° , 点P是弧AB上任意一点(不与点A , B重合),OC⊥AP , OD⊥BP , 垂足分别为C , D , CD= ,则扇形OAB的面积 ( )
A、1个 B、2个 C、3个 D、4个10. 某口罩生产厂2020年1月份平均日产20万个,1月底因防控新冠疫情需求,工厂立即决定从2月份起扩大产能,3月份平均日产量达到45万个,则口罩日产量的月平均增长率是( )A、20% B、30% C、40% D、50%11. 已知二次函数 ,下列叙述中正确的是( )A、图象的开口向上 B、图象的对称轴为直线 C、函数有最小值 D、当 时,函数值 随自变量 的增大而减小12. 若⊙O的内接正n边形的边长与⊙O的半径相等,则 ( )A、6 B、 C、 D、413. 若关于 的一元二次方程 的常数项为 ,则 的值等于( )A、2 B、−2 C、±2 D、−414. 若点 , , 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、15. 如图,在扇形AOB中,∠AOB=90° , 点P是弧AB上任意一点(不与点A , B重合),OC⊥AP , OD⊥BP , 垂足分别为C , D , CD= ,则扇形OAB的面积 ( )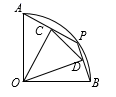 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 用配方法解方程 ,将方程变为 的形式,则 .17. 已知反比例函数y= ,当-3<x<-1时,y的取值范围是.18. 如图,点O是△ABC的内心,将∠ABC平移使顶点B与点O重合,两边与AC分别交于点D和E , 若AB=5,BC=4,AC=7,则△ODE的周长为 .
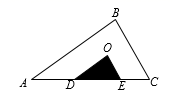 19. 如图,在平面直角坐标系 中,已知点 , 为平面内的动点,且满足 , 为直线 上的动点,则线段 长的最小值为.
19. 如图,在平面直角坐标系 中,已知点 , 为平面内的动点,且满足 , 为直线 上的动点,则线段 长的最小值为.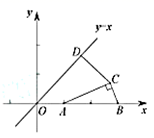
三、解答题
-
20.(1)、解方程:2(x2﹣x)=x2 .(2)、已知方程x2+x+k+1=0有一个根是2,求另一个根.21. 如图,点D是等边三角形ABC内一点,连接DA , DC , 将△DAC绕点A顺时针旋转60°,点D的对应点为点E .
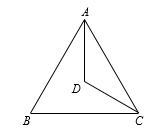 (1)、画出旋转后的图形;(2)、当C , D , E三点共线时,求∠BEC的度数.22. 为了发扬中国航天精神,在中国航天日纪念活动中,学校举行班级歌咏比赛.将分别写有《飞天》《仰望星空》《祖国不会忘记》和《不忘初心》歌名的4张卡片,由一班和二班随机抽取.一班先从中随机抽取1张,放回后再由二班从中随机抽取1张.(1)、写出一班抽中歌曲《祖国不会忘记》的概率.(2)、试用画树状图或列表的方法表示所有可能的结果,求出一班和二班抽中不同歌曲的概率.23. 某学校计划建一个长方形种植园,如图,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).
(1)、画出旋转后的图形;(2)、当C , D , E三点共线时,求∠BEC的度数.22. 为了发扬中国航天精神,在中国航天日纪念活动中,学校举行班级歌咏比赛.将分别写有《飞天》《仰望星空》《祖国不会忘记》和《不忘初心》歌名的4张卡片,由一班和二班随机抽取.一班先从中随机抽取1张,放回后再由二班从中随机抽取1张.(1)、写出一班抽中歌曲《祖国不会忘记》的概率.(2)、试用画树状图或列表的方法表示所有可能的结果,求出一班和二班抽中不同歌曲的概率.23. 某学校计划建一个长方形种植园,如图,种植园的一边靠墙,另三边用周长为30m的篱笆围成,已知墙长为18m,设这个种植园垂直于墙的一边长为x(m),种植园面积为y(m2).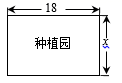 (1)、求 与 的函数关系式,并写出自变量 的取值范围;(2)、根据实际需要,要求这个种植园的面积为100m2 , 求 的值;(3)、当 为多少m时,这个种植园的面积最大,并求出最大值.24. 在平面直角坐标系 中,抛物线 与 轴交于点A , 将点A向右平移2个单位长度,得到点B . 直线 与 轴, 轴分别交于点C , D .
(1)、求 与 的函数关系式,并写出自变量 的取值范围;(2)、根据实际需要,要求这个种植园的面积为100m2 , 求 的值;(3)、当 为多少m时,这个种植园的面积最大,并求出最大值.24. 在平面直角坐标系 中,抛物线 与 轴交于点A , 将点A向右平移2个单位长度,得到点B . 直线 与 轴, 轴分别交于点C , D .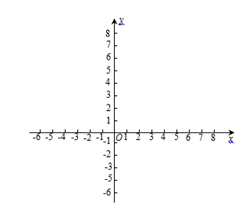
 (1)、该抛物线的对称轴为;(2)、点C的坐标为 , 点D的坐标为;(3)、若点A与点D关于 轴对称:
(1)、该抛物线的对称轴为;(2)、点C的坐标为 , 点D的坐标为;(3)、若点A与点D关于 轴对称:①求点B的坐标;
②若抛物线与线段BC恰有一个公共点,结合函数图象,求 的取值范围.