河北省承德市承德县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 如图,下列角中为俯角的是( )
 A、∠1 B、∠2 C、∠3 D、∠42. 若反比例函数 ( 是常数)的图象在第一、三象限,则 的取值范围是( )A、 B、 C、 D、3. 如图中的几何体是由一个正方体切去一个小正方体后形成的,该几何体的左视图是( )
A、∠1 B、∠2 C、∠3 D、∠42. 若反比例函数 ( 是常数)的图象在第一、三象限,则 的取值范围是( )A、 B、 C、 D、3. 如图中的几何体是由一个正方体切去一个小正方体后形成的,该几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 用配方法将二次函数 化为 的形式为( )A、 B、 C、 D、5. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差S2(单位:千克2)如下表所示:
4. 用配方法将二次函数 化为 的形式为( )A、 B、 C、 D、5. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差S2(单位:千克2)如下表所示:甲
乙
丙
丁
x
24
24
23
20
S2
2.1
1.9
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是( )
A、甲 B、乙 C、丙 D、丁6. 如图,若 与 是位似图形,则位似中心的坐标是( ) A、 B、 C、 D、7. 某口罩加工厂 年一月份口罩产值达 万元,第一季度总产值达 万元,若第二、三月份的月平均增长率为x,则由题意可列方程为( )A、 B、 C、 D、8. 如图,在 中, 为 上一点,若 ,则( )
A、 B、 C、 D、7. 某口罩加工厂 年一月份口罩产值达 万元,第一季度总产值达 万元,若第二、三月份的月平均增长率为x,则由题意可列方程为( )A、 B、 C、 D、8. 如图,在 中, 为 上一点,若 ,则( ) A、 ~ B、 ~ C、 ~ D、无法判断9. 如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.则正方形ABCD与正六边形AEFCGH的周长之比为( )
A、 ~ B、 ~ C、 ~ D、无法判断9. 如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.则正方形ABCD与正六边形AEFCGH的周长之比为( ) A、 ∶ 3 B、 ∶1 C、 ∶ D、1∶10. 一辆汽车匀速通过某段公路,所需时间(h)与行驶速度 (km/h)满足函数关系 点 ,其图象为如图所示的一段双曲线,端点为 和 ,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A、 ∶ 3 B、 ∶1 C、 ∶ D、1∶10. 一辆汽车匀速通过某段公路,所需时间(h)与行驶速度 (km/h)满足函数关系 点 ,其图象为如图所示的一段双曲线,端点为 和 ,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( ) A、 分钟 B、40分钟 C、60分钟 D、 分钟11. 已知点O是△ABC的外心,连接OB,若∠OBC=28°,则∠A的度数为( )
A、 分钟 B、40分钟 C、60分钟 D、 分钟11. 已知点O是△ABC的外心,连接OB,若∠OBC=28°,则∠A的度数为( ) A、28° B、52° C、56° D、62°12. 甲、乙两名同学在一次用频率去估计概率的试验中,统计了某一结果出现的频率,并绘出了如下折线统计图,则最有可能符合这一结果的试验的是( )
A、28° B、52° C、56° D、62°12. 甲、乙两名同学在一次用频率去估计概率的试验中,统计了某一结果出现的频率,并绘出了如下折线统计图,则最有可能符合这一结果的试验的是( ) A、掷一枚正六面体的骰子,出现1点的概率 B、抛一枚硬币,出现正面的概率 C、任意写一个整数,它能被3整除的概率 D、从一副去掉大小王的扑克牌中,任意抽取一张,抽到黑桃的概率13. 如图,在 中,中线 , 相交于点 ,连接 ,给出下列结论∶① ;② ;③ ;④ ;⑤ .其中错误的个数是( )
A、掷一枚正六面体的骰子,出现1点的概率 B、抛一枚硬币,出现正面的概率 C、任意写一个整数,它能被3整除的概率 D、从一副去掉大小王的扑克牌中,任意抽取一张,抽到黑桃的概率13. 如图,在 中,中线 , 相交于点 ,连接 ,给出下列结论∶① ;② ;③ ;④ ;⑤ .其中错误的个数是( ) A、1 B、2 C、3 D、414. 如图,已知 的半径为5,所对的弦AB长为8,点P是 的中点,将 绕点A逆时针旋转90°后得到 ,则在该旋转过程中,点P的运动路径长是( )
A、1 B、2 C、3 D、414. 如图,已知 的半径为5,所对的弦AB长为8,点P是 的中点,将 绕点A逆时针旋转90°后得到 ,则在该旋转过程中,点P的运动路径长是( ) A、 π B、 π C、2 π D、2π15. 如图, 点 , , ,…在射线 上,点 , , ,…在射线 上, , , ,…均为等边三角形,若 ,则边 的长为( )
A、 π B、 π C、2 π D、2π15. 如图, 点 , , ,…在射线 上,点 , , ,…在射线 上, , , ,…均为等边三角形,若 ,则边 的长为( ) A、 B、 C、 D、16. 在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系 中,当 为何值时,抛物线 与直线段 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:
A、 B、 C、 D、16. 在数学活动课上,王老师出示一道数学题目:“在平面直角坐标系 中,当 为何值时,抛物线 与直线段 有唯一公共点或有两个公共点?”某学习小组经探究得到以下四个结论:①当 时,有唯一公共点;②若 为整数,则仅当 的值为4或5或6或7时,才有唯一公共点;③若 为整数,则当 的值为1或2或3时,有两个公共点;④当 时,有两个公共点.其中正确的结论有( )
A、①②④ B、①②③ C、①③ D、①④二、填空题
-
17. 已知关于x的一元二次方程 有一个根为 ,则a的值为 .18. 已知二次函数 中函数y与自变量x之间部分对应值如下表所示,点 在函数图象上
x
…
0
1
2
3
…
y
…
m
n
3
n
…
则表格中的m=;当 时, 和 的大小关系为 .
19. 如图,在 中, , , .点 是 上一动点,以 为斜边向右侧作等腰直角三角形 ,使 ,连接 .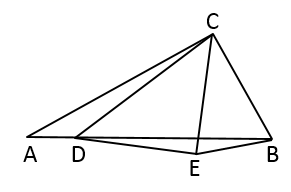 (1)、若点 恰好落在 上,则 的值为;(2)、线段 的最小值为 .
(1)、若点 恰好落在 上,则 的值为;(2)、线段 的最小值为 .三、解答题
-
20. 已知关于 的一元二次方程为 .(1)、当 时,不解方程,判断方程根的情况;(2)、在(1)的条件下,若 ,求解这个方程.21. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
 (1)、求证:△ABD∽△DCE;(2)、若△ABC的边长为9,BD=3,求CE的长.22. 钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”重庆实验外国语学校为鼓励学生抗疫期间在家阅读,组织八年级全体同学参加了疫期居家海量读书活动,随机抽查了部分同学读书本数的情况统计如图所示.
(1)、求证:△ABD∽△DCE;(2)、若△ABC的边长为9,BD=3,求CE的长.22. 钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”重庆实验外国语学校为鼓励学生抗疫期间在家阅读,组织八年级全体同学参加了疫期居家海量读书活动,随机抽查了部分同学读书本数的情况统计如图所示. (1)、本次共抽查学生 ▲ 人,并将条形统计图补充完整;(2)、读书本数的众数是本,中位数是本.(3)、在八年级2000名学生中,读书15本及以上(含15本)的学生估计有多少人?(4)、在八年级六班共有50名学生,其中读书达到25本的有两位男生和两位女生,老师要从这四位同学中随机邀请两位同学分享读书心得,试通过画树状图或列表的方法求恰好是两位男生分享心得的概率.23. 如图,平面直角坐标系中,一次函数 ( )的图象与反比例函数 ( )的图象交于点 和 .
(1)、本次共抽查学生 ▲ 人,并将条形统计图补充完整;(2)、读书本数的众数是本,中位数是本.(3)、在八年级2000名学生中,读书15本及以上(含15本)的学生估计有多少人?(4)、在八年级六班共有50名学生,其中读书达到25本的有两位男生和两位女生,老师要从这四位同学中随机邀请两位同学分享读书心得,试通过画树状图或列表的方法求恰好是两位男生分享心得的概率.23. 如图,平面直角坐标系中,一次函数 ( )的图象与反比例函数 ( )的图象交于点 和 . (1)、求一次函数和反比例函数的表达式;(2)、请直接写出 时x的取值范围;(3)、过点B作 轴, 于点D,点C是直线 上一点,若 ,求点C的坐标.24. 小强洗漱时的侧面示意图如图所示,洗漱台(矩形 )靠墙摆放,高 cm,宽 cm,小强身高166cm,下半身 cm,洗漱时身体前倾,下半身与地面的夹角 ,上半身与下半身所成夹角 ,脚与洗漱台距离 cm,点 , , , 在同一直线上.
(1)、求一次函数和反比例函数的表达式;(2)、请直接写出 时x的取值范围;(3)、过点B作 轴, 于点D,点C是直线 上一点,若 ,求点C的坐标.24. 小强洗漱时的侧面示意图如图所示,洗漱台(矩形 )靠墙摆放,高 cm,宽 cm,小强身高166cm,下半身 cm,洗漱时身体前倾,下半身与地面的夹角 ,上半身与下半身所成夹角 ,脚与洗漱台距离 cm,点 , , , 在同一直线上. (1)、求此时小强腰部点 到墙 的距离.(2)、此时小强头部点 是否恰好在洗漱盆 的中点 的正上方?若是,请说明理由;若不是,则他应向前还是向后移动多少厘米,使头部点 恰好在洗漱盆 的中点 的正上方?(计算过程及结果的长度均精确到1cm.参考数据; , , )25. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如表:
(1)、求此时小强腰部点 到墙 的距离.(2)、此时小强头部点 是否恰好在洗漱盆 的中点 的正上方?若是,请说明理由;若不是,则他应向前还是向后移动多少厘米,使头部点 恰好在洗漱盆 的中点 的正上方?(计算过程及结果的长度均精确到1cm.参考数据; , , )25. 某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如表:售价(元/件)
200
210
220
230
……
月销量(件)
200
180
160
140
……
已知该运动服的进价为每件150元.
(1)、售价为x元,月销量为y件.①求y关于x的函数关系式:
②若销售该运动服的月利润为w元,求w关于x的函数关系式,并求月利润最大时的售价;
(2)、由于运动服进价降低了a元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则a的值是多少?26. 如图,在四边形 中, , , , , , 是 上一点,以点 为圆心的圆切 于点 ,分别交 , 的延长线于点 , ,设 . (1)、当 时,求扇形 的面积;(2)、求 的长;(3)、若 上的点到点 , 的距离均不小于 ,求 的取值范围.
(1)、当 时,求扇形 的面积;(2)、求 的长;(3)、若 上的点到点 , 的距离均不小于 ,求 的取值范围.