河北省沧州市青县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 下列图形中既是中心对称图形又是轴对称图形的是( )A、正三角形 B、正方形 C、正五边形 D、平行四边形2. 把一元二次方程 配方,得 ,则c和m的值分别是( )A、c=5,m=4 B、c=10,m=6 C、c=﹣5,m=﹣4 D、c=3,m=83. 用长分别为3cm,4cm,5cm的三条线段可以围成直角三角形的事件是( )A、必然事件 B、不可能事件 C、随机事件 D、以上都不是4. 如果(x﹣y﹣2)(x﹣y+1)=0,那么x﹣y=( )A、2 B、﹣1 C、2或﹣1 D、﹣2或15. 如图, 内接于 , 是 是直径, 平分 交 于 点,则 等于( )
 A、 B、 C、 D、6. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )
A、 B、 C、 D、6. 如图,某水库堤坝横断面迎水坡AB的坡比是1: ,堤坝高BC=50m,则应水坡面AB的长度是( )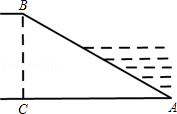 A、100m B、100 m C、150m D、50 m7. 如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2 , 设小路的宽为xm,那么x满足的方程是( )
A、100m B、100 m C、150m D、50 m7. 如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2 , 设小路的宽为xm,那么x满足的方程是( ) A、2x2-25x+16=0 B、x2-25x+32=0 C、x2-17x+16=0 D、x2-17x-16=08. 已知反比例函数 ,下列结论错误的是( )A、其图象经过点(-2,1) B、其图象位于第二、第四象限 C、当x <0时,y随x的增大而增大 D、当x>-1时,y>-29. 如图,PA、PB分别切圆O于点A、B,∠P=70°,则∠C=( )
A、2x2-25x+16=0 B、x2-25x+32=0 C、x2-17x+16=0 D、x2-17x-16=08. 已知反比例函数 ,下列结论错误的是( )A、其图象经过点(-2,1) B、其图象位于第二、第四象限 C、当x <0时,y随x的增大而增大 D、当x>-1时,y>-29. 如图,PA、PB分别切圆O于点A、B,∠P=70°,则∠C=( ) A、70° B、55° C、110° D、140°10. 三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,AA′=30cm,则三角尺与它在墙上影子的周长比是( )
A、70° B、55° C、110° D、140°10. 三角尺在灯泡O的照射下在墙上形成的影子如图所示.若OA=20cm,AA′=30cm,则三角尺与它在墙上影子的周长比是( ) A、4:9 B、2:3 C、4:25 D、2:511. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、
A、4:9 B、2:3 C、4:25 D、2:511. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、 B、
B、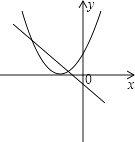 C、
C、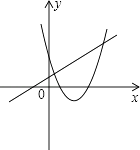 D、
D、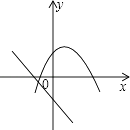 12. 若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为( )
12. 若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为( )
A、120° B、180° C、240° D、300°13. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )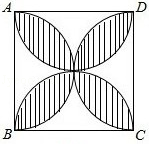 A、 B、 C、 D、14. 如图,△ABO的顶点A在函数y= (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为( )
A、 B、 C、 D、14. 如图,△ABO的顶点A在函数y= (x>0)的图象上,∠ABO=90°,过AO边的三等分点M、N分别作x轴的平行线交AB于点P、Q.若四边形MNQP的面积为3,则k的值为( )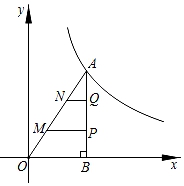 A、9 B、12 C、15 D、1815. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、9 B、12 C、15 D、1815. 如图, 中, ,点D在 上, .若 ,则 的长度为( )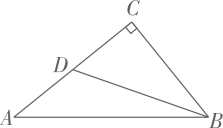 A、 B、 C、 D、416. 如图是二次函数 图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
A、 B、 C、 D、416. 如图是二次函数 图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;
②若点B( , )、C( , )为函数图象上的两点,则 ;
③2a﹣b=0;
④ <0,其中,正确结论的个数是( )
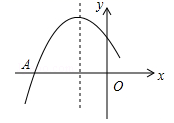 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
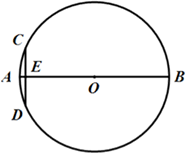
17.(1)、抛物线 的顶点坐标是 .(2)、关于 的一元二次方程 的根的情况是18. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何?”转化为现在的数学语言就是:如图, 是 的直径,弦 ,垂足为 , 寸, 寸.则直径 的长为寸.
 19. 已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:
19. 已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足如表:x
…
0
1
2
3
4
5
…
y
…
3
0
1
0
m
8
…
(1)、可求得m的值为;(2)、求出这个二次函数的解析式;(3)、当0<x<3时,则y的取值范围为 .三、解答题
-
20. 如图所示,△ABC三个顶点的坐标分别为A(-4,4),B(-2,0),C(-1,2).
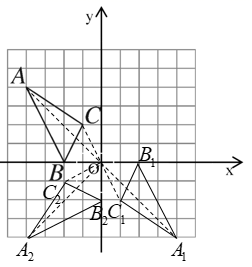
⑴如果△A1B1C1与△ABC关于原点中心对称,画出△A1B1C1并写出A1 , B1 , C1三点的坐标;
⑵画出将△ABC绕原点O按逆时针方向旋转 所得的△A2B2C2 .
21. 一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).(1)、小红摸出标有数3的小球的概率是 .(2)、请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.(3)、求点P(x,y)在函数y=﹣x+5图象上的概率.22. 如图反比例函数 与一次函数 的图象交于点A(1,3)和B(﹣3,n)两点. (1)、求反比例函数与一次函数的解析式;(2)、由图象直接写出当x取什么值时,一次函数的值大于反比例函数的值.(3)、连OA、OB,求出△OAB的面积.23. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)
(1)、求反比例函数与一次函数的解析式;(2)、由图象直接写出当x取什么值时,一次函数的值大于反比例函数的值.(3)、连OA、OB,求出△OAB的面积.23. 构建几何图形解决代数问题是“数形结合”思想的重要策略.在计算 时,如图,在 中, ,延长 使 ,连接 ,得 ,所以 ,类比这种方法,计算 (画图并写出过程)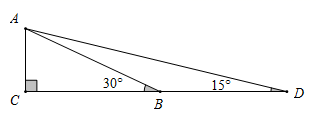 24. 在 中,弦 与直径 相交于点P , .
24. 在 中,弦 与直径 相交于点P , .

(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点D作 的切线,与 的延长线相交于点E , 求 的大小.
25. 如图,抛物线y=x2+bx+c经过点(3,12)和(﹣2,﹣3),与两坐标轴的交点分别为A,B,C,它的对称轴为直线l.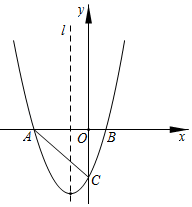 (1)、求该抛物线的表达式;(2)、P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.26. 如图1,在矩形ABCD中,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
(1)、求该抛物线的表达式;(2)、P是该抛物线上的点,过点P作l的垂线,垂足为D,E是l上的点.要使以P、D、E为顶点的三角形与△AOC全等,求满足条件的点P,点E的坐标.26. 如图1,在矩形ABCD中,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.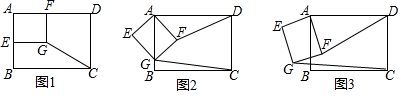 (1)、请直接写出CG的长是 .(2)、如图2,当矩形AEGF绕点A旋转(比如顺时针)至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.(提示:可作FP⊥AD于P)(3)、当矩形AEGF绕点A旋转至如图3的位置时,(2)中DF与CG之间的数量关系是否还成立?请说明理由.(提示:可连接AG和AC)
(1)、请直接写出CG的长是 .(2)、如图2,当矩形AEGF绕点A旋转(比如顺时针)至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.(提示:可作FP⊥AD于P)(3)、当矩形AEGF绕点A旋转至如图3的位置时,(2)中DF与CG之间的数量关系是否还成立?请说明理由.(提示:可连接AG和AC)