河北省保定市曲阳县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 如图,梯子(长度不变)跟地面所成的锐角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
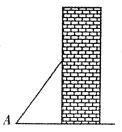 A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关2. 如果矩形的面积为6cm2 , 那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )A、
A、sinA的值越大,梯子越陡 B、cosA的值越大,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的三角函数值无关2. 如果矩形的面积为6cm2 , 那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( )A、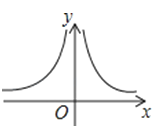 B、
B、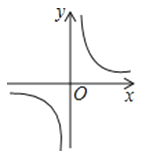 C、
C、 D、
D、 3. 在二次函数 中,函数值y与自变量x的部分对应值如下表 则m的值为( ).
3. 在二次函数 中,函数值y与自变量x的部分对应值如下表 则m的值为( ).x
-2
-1
0
1
2
3
4
y
7
2
-1
-2
m
2
7
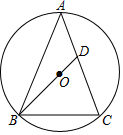
A、1 B、-1 C、2 D、-24. 如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.下列四个角中,一定与∠ACD互余的角是( )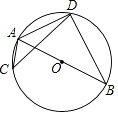 A、∠ADC B、∠ABD C、∠BAC D、∠BAD5. 如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC , 若sinC= ,BC=12,求AD的长( )
A、∠ADC B、∠ABD C、∠BAC D、∠BAD5. 如图,在△ABC中,AD是BC上的高,tan∠B=cos∠DAC , 若sinC= ,BC=12,求AD的长( )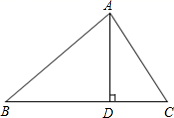 A、13 B、12 C、8 D、无法判断6. 某地统计部门公布最近5年国民消费指数增长率分别为8.5%、9.2%、9.9%、10.2%、9.8%,业内人士评论说:“这五年消费指数增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”说明这组数据中比较小的是( )A、方差 B、平均数 C、众数 D、中位数7. 探究性学习小组的同学接受了测量同样型号圆柱工件直径的任务.他们使用的工具是有一个角是60°的直角三角板和刻度尺.小明的测量方法如图甲所示.测得PC=12cm.小亮的测量方法如图乙所示.则与QA的值最接近的是( )
A、13 B、12 C、8 D、无法判断6. 某地统计部门公布最近5年国民消费指数增长率分别为8.5%、9.2%、9.9%、10.2%、9.8%,业内人士评论说:“这五年消费指数增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”说明这组数据中比较小的是( )A、方差 B、平均数 C、众数 D、中位数7. 探究性学习小组的同学接受了测量同样型号圆柱工件直径的任务.他们使用的工具是有一个角是60°的直角三角板和刻度尺.小明的测量方法如图甲所示.测得PC=12cm.小亮的测量方法如图乙所示.则与QA的值最接近的是( ) A、8cm B、7 cm C、6 cm D、5 cm8. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )
A、8cm B、7 cm C、6 cm D、5 cm8. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )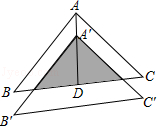 A、2 B、3 C、 D、9. 如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm , ⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( )
A、2 B、3 C、 D、9. 如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm , ⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为( ) A、12 cm B、7 cm C、6 cm D、随直线MN的变化而变化10. 如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣ x2刻画,斜坡可以用一次函数y= x刻画,下列结论错误的是( )
A、12 cm B、7 cm C、6 cm D、随直线MN的变化而变化10. 如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣ x2刻画,斜坡可以用一次函数y= x刻画,下列结论错误的是( )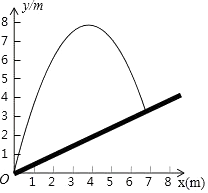 A、当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m B、小球距O点水平距离超过4米呈下降趋势 C、小球落地点距O点水平距离为7米 D、斜坡的坡度为1:2
A、当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m B、小球距O点水平距离超过4米呈下降趋势 C、小球落地点距O点水平距离为7米 D、斜坡的坡度为1:2二、填空题
-
11. 当x=时,代数式x2-13x+12的值等于012. cos60°的值等于 .13. 在平面直角坐标系 中,直线 与双曲线 交于A,B两点.若点A,B的纵坐标分别为 ,则 的值为 .14. 如图,四边形OABC是菱形,点B,C在以点O为圆心的弧EF上,且∠1=∠2,若菱形边OA=3,则扇形OEF的面积为
 15. 如图,在矩形ABCD中,过点B作对角线AC的垂线,交AD于点E , 若AB=2,BC=4,则AE= .
15. 如图,在矩形ABCD中,过点B作对角线AC的垂线,交AD于点E , 若AB=2,BC=4,则AE= .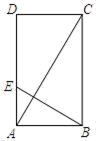 16. 已知二次函数y=ax2﹣4ax+4,当x分别取x1、x2两个不同的值时,函数值相等,则当x取x1+x2时,y的值为17. 如图所示,已知⊙O的半径为5,弦AB , CD所对的圆心角分别是∠AOB , ∠COD . 若∠AOB与∠COD互补,弦CD=6,则弦AB的长为 .
16. 已知二次函数y=ax2﹣4ax+4,当x分别取x1、x2两个不同的值时,函数值相等,则当x取x1+x2时,y的值为17. 如图所示,已知⊙O的半径为5,弦AB , CD所对的圆心角分别是∠AOB , ∠COD . 若∠AOB与∠COD互补,弦CD=6,则弦AB的长为 . 18. 若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣ 的图象上,则y1 , y2 , y3的大小关系是.19. 如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2( +1)m.工人师傅搬运此钢架(填“能”或“不能”)通过一个直径为2.1m的圆形门?
18. 若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣ 的图象上,则y1 , y2 , y3的大小关系是.19. 如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2( +1)m.工人师傅搬运此钢架(填“能”或“不能”)通过一个直径为2.1m的圆形门? 20. 如图,抛物线y= (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的是(填序号)
20. 如图,抛物线y= (x+2)(x﹣8)与x轴交于A,B两点,与y轴交于点C,顶点为M,以AB为直径作⊙D.下列结论:①抛物线的对称轴是直线x=3;②⊙D的面积为16π;③抛物线上存在点E,使四边形ACED为平行四边形;④直线CM与⊙D相切.其中正确结论的是(填序号)
三、解答题
-
21. 已知x1 , x2是关于x的一元二次方程 的两实数根.(1)、求m的范围;(2)、若 ,求m的值;(3)、已知等腰△ABC的一边长为7,若x1 , x2恰好是△ABC另外两边的边长,求这个三角形的周长.22. 随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
 (1)、如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是什么;(2)、机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,角度精确到度;参考数据:sin49°≈0.75,cos37°≈0.80,tan37°≈0.75)23. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
(1)、如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是什么;(2)、机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,角度精确到度;参考数据:sin49°≈0.75,cos37°≈0.80,tan37°≈0.75)23. 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:.小云所住小区5月1日至30日的厨余垃圾分出量统计图:

.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段
1日至10日
11日至20日
21日至30日
平均数
100
170
250
(1)、该小区5月1日至30日的厨余垃圾分出量的平均数约为(结果取整数)(2)、已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的倍(结果保留小数点后一位);(3)、记该小区5月1日至10日的厨余垃圾分出量的方差为 5月11日至20日的厨余垃圾分出量的方差为 ,5月21日至30日的厨余垃圾分出量的方差为 .直接写出 的大小关系.24. 如图,已知A ,B(-1,2)是一次函数 与反比例函数( )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
 (1)、根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)、求一次函数解析式及m的值;(3)、P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
(1)、根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)、求一次函数解析式及m的值;(3)、P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.