北京市东城区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-10-09 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、直角三角形 B、圆 C、等边三角形 D、四边形2. 在平面直角坐标系 中,下列函数的图象上存在点 的是( )A、 B、 C、 D、3. 若关于 的方程 的一个根是-1,则 的值是( )A、1 B、-1 C、 D、-34. 若菱形的面积为定值,则它的一条对角线的长与另一条对角线的长满足的函数关系是( )A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系5. 在平面直角坐标系 中, 与 关于原点 成中心对称的是( )A、
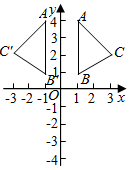 B、
B、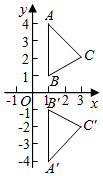 C、
C、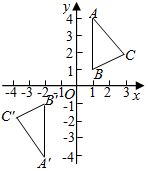 D、
D、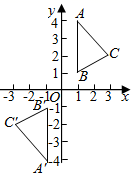 6. 不透明的袋子里有50张2022年北京冬奥会宣传卡片,卡片上印有会徽、吉祥物冰墩墩、吉祥物雪容融图案,每张卡片只有一种图案除图案不同外其余均相同,其中印有冰墩墩的卡片共有 张.从中随机摸出1张卡片,若印有冰墩墩图案的概率是 ,则 的值是( )A、250 B、10 C、5 D、17. 如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为 ,设交点为 ,点 之间有一座假山.为了测量 之间的距离,小明已经测量了线段 和 的长度,只需再测量一条线段的长度,就可以计算 之间的距离.小明应该测量的是( )
6. 不透明的袋子里有50张2022年北京冬奥会宣传卡片,卡片上印有会徽、吉祥物冰墩墩、吉祥物雪容融图案,每张卡片只有一种图案除图案不同外其余均相同,其中印有冰墩墩的卡片共有 张.从中随机摸出1张卡片,若印有冰墩墩图案的概率是 ,则 的值是( )A、250 B、10 C、5 D、17. 如图,在圆形花圃中有两条笔直的小径,两端都在花圃边界上,分别记为 ,设交点为 ,点 之间有一座假山.为了测量 之间的距离,小明已经测量了线段 和 的长度,只需再测量一条线段的长度,就可以计算 之间的距离.小明应该测量的是( )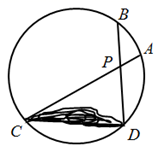 A、线段 B、线段 C、线段 D、线段8. 如图所示,在矩形纸片上剪下一个扇形和一个圆形,使之恰好能围成一个圆锥模型.若扇形的半径为 ,圆的半径为 ,则 与 满足的数量关系是( )
A、线段 B、线段 C、线段 D、线段8. 如图所示,在矩形纸片上剪下一个扇形和一个圆形,使之恰好能围成一个圆锥模型.若扇形的半径为 ,圆的半径为 ,则 与 满足的数量关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
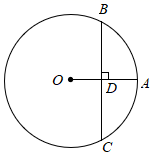
9. 写出一个二次函数,使其满足:①图象开口向下;②当 时, 随着 的增大而减小.这个二次函数的解析式可以是 .10. 如图,点 在 上,弦 垂直平分 ,垂足为 .若 ,则 的长为 .
 11. 盒中有2个黄球、1个白球, 盒中有1个黄球、1个白球,这些球除颜色外无其他差别.分别从每个盒中随机取出1个球,取出的2个球都是白球的概率是 .12. 2017年生产1吨某种商品的成本是3000元,由于原料价格上涨,两年后,2019年生产1吨该商品的成本是5000元,求该种商品成本的年平均增长率.设年平均增长率为 ,则所列的方程应为(不增加其它未知数).13. 在平面直角坐标系 中,将抛物线 沿着 轴平移2个单位长度,所得抛物线的解析式为 .14. 如图, 是等边三角形.若将 绕点 逆时针旋转角 后得到 ,连接 和 ,则 的度数为 .
11. 盒中有2个黄球、1个白球, 盒中有1个黄球、1个白球,这些球除颜色外无其他差别.分别从每个盒中随机取出1个球,取出的2个球都是白球的概率是 .12. 2017年生产1吨某种商品的成本是3000元,由于原料价格上涨,两年后,2019年生产1吨该商品的成本是5000元,求该种商品成本的年平均增长率.设年平均增长率为 ,则所列的方程应为(不增加其它未知数).13. 在平面直角坐标系 中,将抛物线 沿着 轴平移2个单位长度,所得抛物线的解析式为 .14. 如图, 是等边三角形.若将 绕点 逆时针旋转角 后得到 ,连接 和 ,则 的度数为 . 15. 已知抛物线 与直线 相交于 两点,若点 的横坐标 ,则点 的横坐标 的值为 .16. 如图1,在 中, 是边 上一动点,设 两点之间的距离为 两点之间的距离为 ,表示 与 的函数关系的图象如图2所示.则线段 的长为 , 线段 的长为 .
15. 已知抛物线 与直线 相交于 两点,若点 的横坐标 ,则点 的横坐标 的值为 .16. 如图1,在 中, 是边 上一动点,设 两点之间的距离为 两点之间的距离为 ,表示 与 的函数关系的图象如图2所示.则线段 的长为 , 线段 的长为 .
三、解答题
-
17. 已知:如图线段 .

求作:以 为斜边的直角 ,使得一个内角等于30°.
作法:①作线段 的垂直平分线交 于点 ;
②以点 为圆心, 长为半径画圆;
③以点 为圆心, 长为半径画弧,与 相交,
记其中一个交点为 ;
④分别连接 .
就是所求作的直角三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接 ,
是 的直径,
▲ °( ▲ )(填推理的依据).
是以 为斜边的直角三角形.
,
是等边三角形.
.
▲ °.
18. 在平面直角坐标系 中,二次函数的图象与 轴交于点 ,且过点 .(1)、求二次函数的解析式;(2)、当 时,求 的取值范围.19. 如图, 平分 ,作 交 于点 ,点 在 的延长线上, , 的延长线交 于点 .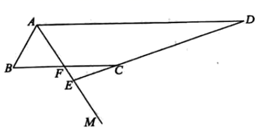 (1)、求证: ;(2)、若 ,求 的值.20. 关于 的一元二次方程 .(1)、若方程有两个相等的实数根用含 的代数式表示 ;(2)、若方程有两个不相等的实数根,且 .
(1)、求证: ;(2)、若 ,求 的值.20. 关于 的一元二次方程 .(1)、若方程有两个相等的实数根用含 的代数式表示 ;(2)、若方程有两个不相等的实数根,且 .①求 的取值范围;
②写出一个满足条件的 的值,并求此时方程的根.
21. 在平面直角坐标系 中,已知双曲线 过点 ,与直线 交于 两点(点 的横坐标小于点 的横坐标). (1)、求 的值;(2)、求点 的坐标;(3)、若直线 与双曲线 交于点 ,与直线 交于点 .当 时,写出 的取值范围.22. 如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 .
(1)、求 的值;(2)、求点 的坐标;(3)、若直线 与双曲线 交于点 ,与直线 交于点 .当 时,写出 的取值范围.22. 如图,在 中, 平分 ,交 于点 ,以点 为圆心, 长为半径画 . (1)、补全图形,判断直线 与 的位置关系,并证明;(2)、若 ,求 的半径.23. 在平面直角坐标系 中已知抛物线 .(1)、若此抛物线经过点 ,求 的值;(2)、求抛物线的顶点坐标(用含 的式子表示);(3)、若抛物线上存在两点 和 ,且 ,求 的取值范围.24. 在 中, 于点 .
(1)、补全图形,判断直线 与 的位置关系,并证明;(2)、若 ,求 的半径.23. 在平面直角坐标系 中已知抛物线 .(1)、若此抛物线经过点 ,求 的值;(2)、求抛物线的顶点坐标(用含 的式子表示);(3)、若抛物线上存在两点 和 ,且 ,求 的取值范围.24. 在 中, 于点 .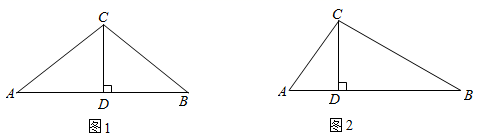 (1)、如图1,当点 是线段 的中点时,
(1)、如图1,当点 是线段 的中点时,① 的长为;
②延长 至点 ,使得 ,此时 与 的数量关系是 , 与 的数量关系是;
(2)、如图2,当点 不是线段 的中点时,画 (点 与点 在直线 的异侧),使 ,连接 .①按要求补全图形;
②求 的长.
25. 在平面直角坐标系 中, 的半径为1.给出如下定义:记线段 的中点为 ,当点 不在 上时,平移线段 ,使点 落在 上,得到线段 ( 分别为点 的对应点)线段 长度的最小值称为线段 到 的“平移距离”.
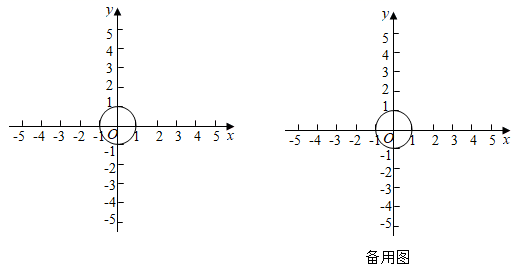 (1)、已知点 的坐标为 ,点 在 轴上.
(1)、已知点 的坐标为 ,点 在 轴上.①若点 与原点 重合,则线段 到 的“平移距离”为;
②若线段 到 的“平移距离”为2,则点 的坐标为;
(2)、若点 都在直线 上,且 ,记线段 到 的“平移距离”为 ,求 的最小值;(3)、若点 的坐标为 ,且 ,记线段 到 的“平移距离”为 ,直接写出 的取值范围.