甘肃省兰州市第四片区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-10-09 类型:期中考试
一、单选题
-
1. 下列各数中,3.14159, ,0.131131113…(相邻两个3之间1的个数逐次加1个), , , ,无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 若式子 在实数范围内有意义,则 x的取值范围是( )A、x>1 B、x>﹣1 C、x≥1 D、x≥﹣13. 如图为5×5的正方形格子,其中所有线段的端点都在格点上,长度是无理数的线段有 ( )
 A、b、c、d B、c、d C、a、d D、b、c4. 直线y=x﹣1的图象经过的象限是( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限5. 以下列各组数据为三角形三边,能构成直角三角形的是( )A、4cm,8cm,7cm B、3cm,5cm,2cm C、2cm,2cm,4cm D、13cm,12cm,5cm6. 如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.
A、b、c、d B、c、d C、a、d D、b、c4. 直线y=x﹣1的图象经过的象限是( )A、第一、二、三象限 B、第一、二、四象限 C、第二、三、四象限 D、第一、三、四象限5. 以下列各组数据为三角形三边,能构成直角三角形的是( )A、4cm,8cm,7cm B、3cm,5cm,2cm C、2cm,2cm,4cm D、13cm,12cm,5cm6. 如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.
a.运动员推出去的铅球(铅球的高度与时间的关系);
b.静止的小车从光滑的斜面滑下(小车的速度与时间的关系);
c.一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系);
d.小明从A地到B地后,停留一段时间,然后按原来的速度原路返回(小明离A地的距离与时间的关系).
正确的顺序是( )
A、abcd B、abdc C、acbd D、acdb7. 下列四组点中,可以在同一个正比例函数图象上的一组点是( )A、(2.-3),(-4,6) B、(-2,3),(4,6) C、(-2,-3),(4,-6) D、(2, 3),(-4,6)8. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、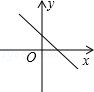 B、
B、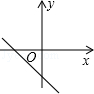 C、
C、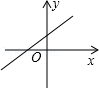 D、
D、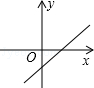 9. 如图,以数轴的单位长度线段为边作一个正方形,以表示数0的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
9. 如图,以数轴的单位长度线段为边作一个正方形,以表示数0的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )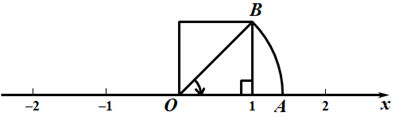 A、 B、 C、 D、10. 若一直角三角形两边长分别为4和5,则第三边长为 ( )A、3 B、3或 C、6或3 D、11. 下列运算中错误的有多少个( )
A、 B、 C、 D、10. 若一直角三角形两边长分别为4和5,则第三边长为 ( )A、3 B、3或 C、6或3 D、11. 下列运算中错误的有多少个( )① =4 ② ③ =﹣3 ④ =3 ⑤± =3.
A、4 B、3 C、2 D、112. 如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 4的平方根是14. 点 到x轴的距离是 , 到y轴的距离是 , 到原点的距离是.15. 在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B, 的面积为.16. 点 , 是一次函数 图象上的两点,则 .(填“ ”、“ ”或“ ”).17. 实数 、 在数轴上的位置,化简 .

三、解答题
-
18. 计算:(1)、(2)、19. 已知点 和 .试根据下列条件求出a,b的值.(1)、A,B两点关于y轴对称;(2)、A,B两点关于x轴对称;(3)、AB‖x轴20. 如图是美国总统Garfield于1876年给出的一种验证勾股定理的办法,你能利用它证明勾股定理吗?请写出你的证明过程.(提示:如图三个三角形均是直角三角形)
 21. 矩形的周长是 ,设一边长为 ,另一边长为 .
21. 矩形的周长是 ,设一边长为 ,另一边长为 . (1)、求y关于x的函数关系式,并写出自变量x的取值范围;(2)、在如图所示的平面直角坐标系中,作出所求函数的图象.22. 如图:在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
(1)、求y关于x的函数关系式,并写出自变量x的取值范围;(2)、在如图所示的平面直角坐标系中,作出所求函数的图象.22. 如图:在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积. 23. 为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过 时,水费按每立方米1.1元收费,超过 时,超过部分每立方米按1.6元收费,设每户每月用水量为 ,应缴水费为y元.(1)、写出y与x之间的函数表达式;(2)、如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?24. 如图,某储藏室入口的截面是一个半径为1.2米的半圆形,一个长、宽、高分别是1.2m,1m,0.8m的箱子能放进储藏室吗?请说明理由.
23. 为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过 时,水费按每立方米1.1元收费,超过 时,超过部分每立方米按1.6元收费,设每户每月用水量为 ,应缴水费为y元.(1)、写出y与x之间的函数表达式;(2)、如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?24. 如图,某储藏室入口的截面是一个半径为1.2米的半圆形,一个长、宽、高分别是1.2m,1m,0.8m的箱子能放进储藏室吗?请说明理由. 25. 在平面直角坐标系中,已知点M的坐标为 .(1)、若点M在x轴上,求m的值;(2)、已知点N的坐标为 ,且直线 轴,求线段 的长.
25. 在平面直角坐标系中,已知点M的坐标为 .(1)、若点M在x轴上,求m的值;(2)、已知点N的坐标为 ,且直线 轴,求线段 的长.

