江苏省扬州市江都区八校联谊2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期:2021-10-09 类型:月考试卷
一、单选题
-
1. 下列说法中,正确的是( )A、所有的等腰三角形都相似 B、所有的菱形都相似 C、所有的矩形都相似 D、所有的等腰直角三角形都相似2. 已知 ,且 ,则 等于( )A、 B、 C、 D、3. 期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”.上面两位同学的话能反映出的统计量分别是( )A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数4. 已知圆锥的底面半径为6,母线长为8,圆锥的侧面积为( )A、60 B、48 C、60π D、48π5. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片,如果全班有x名学生,根据题意,列出方程为( )A、x(x-1)=2070 B、x(x+1)=2070 C、2x(x+1)=2070 D、 =20706. 已知点 、 , 在函数 的图象上,则 的大小关系为( )A、 B、 C、 D、7. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a =2;④方程ax2+bx+c=0有两个相等的实数根.其中正确结论的个数为( )
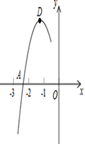 A、1个 B、2个 C、3个 D、4个8. 如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是( )
A、1个 B、2个 C、3个 D、4个8. 如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是( )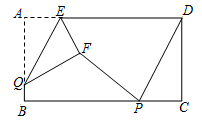 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 当 时,函数 是关于 的二次函数.10. 已知 ,且 ,则 的值为.11. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比,已知这本书的长为20cm,则它的宽约为cm.(精确到0.1cm)12. 若m是方程2x2﹣3x﹣1=0的一个根,则6m2﹣9m+2017的值为.13. 把二次函数y=2x2的图象向左平移1个单位长度,再向下平移2个单位长度,平移后抛物线的解析式为 .
14. 某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=60x﹣1.5x2 , 该型号飞机着陆后滑行m才能停下来.15. 抛物线y= ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:x
...
-3
-2
- 1
0
1
...
y
...
-6
0
4
6
6
...
容易看出,(-2,0)是抛物线与x轴的一个交点,则它与x轴的另一个交点的坐标为.
16. 如图,AB,AC分别是☉O的直径和弦,OD⊥AC于点D,连接BD,BC,AB=5,AC=4,则BD=.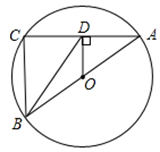 17. 若二次函数 的图象如图所示,则不等式 的解集为.
17. 若二次函数 的图象如图所示,则不等式 的解集为.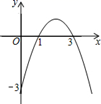 18. 如图, 的顶点 在抛物线 上,将 绕点 顺时针旋转 得到 ,现将抛物线沿 轴向上平移 个单位,使得抛物线与边 只有一个公共点 ,则 的取值范围为.
18. 如图, 的顶点 在抛物线 上,将 绕点 顺时针旋转 得到 ,现将抛物线沿 轴向上平移 个单位,使得抛物线与边 只有一个公共点 ,则 的取值范围为.
三、解答题
-
19. 解下列方程:(1)、 ;(2)、 .20. 已知关于 的一元二次方程 .(1)、求证:方程一定有两个实数根;(2)、若此方程的两根为不相等的整数,求正整数 的值.21. 某中学为了宣传防疫知识,在该校七、八两个年级开展了“防疫知识”大赛活动.为了了解参赛学生的成绩,从两个年级中各随机选取了10名学生的成绩,数据如下:
七年级:92,97,88,92,94,95,92,95,97,98;
八年级:93,94,88,91,92,93,100,98,98,93.
通过整理,得到如下所示的数据分析表.
项目
平均分
中位数
众数
方差
七年级
94.5
92
8.4
八年级
94
93
(1)、填空: , ;(2)、通过计算说明哪个年级的成绩更稳定;(3)、学校规定,成绩不低于96分的选手可以获奖,若该校七年级有300人参加比赛,请估计七年级有多少人获奖.22. 防疫期间,全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道,某天早晨,该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是;(2)、利用画树状图或列表的方法,求小明和小丽从同一个测温通道通过的概率.23. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F .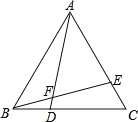 (1)、试说明△ABD≌△BCE;(2)、△EAF与△EBA相似吗?说说你的理由.24. 如图, 是圆O的弦, 是圆 外一点, , 交 于点P,交圆O于点D,且 .
(1)、试说明△ABD≌△BCE;(2)、△EAF与△EBA相似吗?说说你的理由.24. 如图, 是圆O的弦, 是圆 外一点, , 交 于点P,交圆O于点D,且 .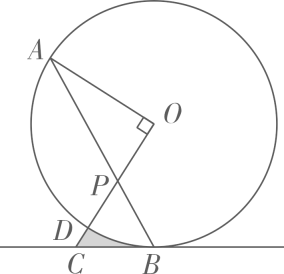 (1)、判断直线 与圆O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.25. 进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.(1)、试确定周销售量 (包)与售价 (元/包)之间的函数关系式并写出 的取值范围;(2)、当售价 (元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润 (元)最大?最大利润是多少?26. 如图,抛物线 的顶点为 ,且抛物线与直线 相交于 两点,且点 在 轴上,点 的坐标为 ,连接 .
(1)、判断直线 与圆O的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.25. 进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.(1)、试确定周销售量 (包)与售价 (元/包)之间的函数关系式并写出 的取值范围;(2)、当售价 (元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润 (元)最大?最大利润是多少?26. 如图,抛物线 的顶点为 ,且抛物线与直线 相交于 两点,且点 在 轴上,点 的坐标为 ,连接 .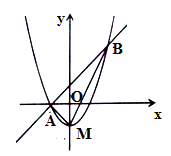 (1)、 , , (直接写出结果);(2)、当 时,则 的取值范围为(直接写出结果);(3)、在直线 下方的抛物线上是否存在一点 ,使得 的面积最大?若存在,求出 的最大面积及点 坐标.27. 阅读下列材料,完成文后任务:
(1)、 , , (直接写出结果);(2)、当 时,则 的取值范围为(直接写出结果);(3)、在直线 下方的抛物线上是否存在一点 ,使得 的面积最大?若存在,求出 的最大面积及点 坐标.27. 阅读下列材料,完成文后任务:克罗狄斯·托勒密(约公元 年—公元 年),希腊著名的天文学家、地理学家和光学家.在数学方面,他论证了四边形的特性,即著名的托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边的乘积之和.
用数学文字表示为:如图1,已知四边形 内接于 ,则
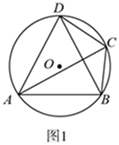
任务:
(1)、如图1,当 为等边三角形时, 与 有怎样的数量关系?并说明理由;(2)、如图2,已知 为直径, , ,求 的长; (3)、如图3,在四边形 中, , , ,则 的面积为.
(3)、如图3,在四边形 中, , , ,则 的面积为. 28. 如图,在矩形 中,点 、点 分别在 轴和 轴上,点 .抛物线 经过 两点,交 的延长线于点 ,与 轴另一个交点为 ,且 .
28. 如图,在矩形 中,点 、点 分别在 轴和 轴上,点 .抛物线 经过 两点,交 的延长线于点 ,与 轴另一个交点为 ,且 . (1)、求抛物线的表达式;(2)、点 是直线 上方抛物线上的一个动点, 轴, ,垂足为 .
(1)、求抛物线的表达式;(2)、点 是直线 上方抛物线上的一个动点, 轴, ,垂足为 .①猜想: 与 的数量关系,并证明你的猜想;
②设 的长为 ,点 的横坐标为 ,求 与 的函数表达式,并求 的最大值.
(3)、如果 是抛物线对称轴上一点,在抛物线上是否存在一点 ,使得以 为顶点的四边形是平行四边形?若存在,直接写出点 的坐标;若不存在,请说明理由.