江苏省东台市第五联盟2020-2021学年八年级上学期数学第二次月考试卷

试卷更新日期：2021-10-09 类型：月考试卷

进入出卷网下载

一、单选题

1. －2的绝对值是（）

A、2 B、－2 　　 C、 $\frac{1}{2}$ 　 D、－ $\frac{1}{2}$

查看试题解析
2. 已知点Q在第三象限，且到y轴的距离为2，则点Q的坐标可能为（）

A、（4，﹣2） B、（﹣4，﹣2） C、（2，4） D、（﹣2，﹣4）

查看试题解析
3. 在﹣0.101001， $\sqrt{8}$ ， $\sqrt[3]{8}$ ，﹣ $\frac{π}{2}$ ，0， $\frac{13}{7}$ 中无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列条件不能判定一个三角形为直角三角形的是（）

A、三个内角之比为1︰2︰3 B、一边上的中线等于该边的一半 C、三边为 $\frac{1}{12} ， \frac{1}{13} ， \frac{1}{5}$ D、三边长为 $m^{2} + n^{2} 、 m^{2} - n^{2} 、 2 m n (m > n > 0)$

查看试题解析
5. 在等腰△ABC中，AB=AC，中线BD将这个三角形的周长分为9和12两个部分，则这个等腰三角形的腰长为（）

A、5 B、8 C、5或9 D、6或8

查看试题解析
6. 已知等腰三角形的一个角是100°，则它的顶角是（）

A、40° B、60° C、80° D、100°

查看试题解析
7. 如图，在平面直角坐标系中，A(-8，-1)，B(-6，-9)，C(-2，-9)，D(-4，-1)先将四边形ABCD沿x轴翻折，再向右平移8个单位长度，向下平移1个单位长度后，得到四边形A₁B₁C₁D₁ ，最后将四边形A₁B₁C₁D₁ ，绕着A₁旋转，使旋转后的四边形对角线的交点落在x轴上，则旋转后的四边形对角线交点坐标为（）

A、(4 ，0) B、(5，0) C、(4，0)或 (5，0) D、(5，0)或(-5，0)

查看试题解析

二、填空题

8. 函数 $y = \sqrt{x - 1}$ 中自变量x的取值范围是.

查看试题解析
9. 在平面直角坐标系中，点A（﹣4，4）关于x轴的对称点B的坐标为．

查看试题解析
10. 太阳半径约为696000千米，数字696000用科学记数法表示为千米.

查看试题解析
11. 直角三角形的两边长分别为6和8，则该直角三角形斜边上的中线为.

查看试题解析
12. 若点A的坐标（x，y）满足条件(x－3)²＋ $\sqrt{y + 2}$ ＝0，则点A在第象限

查看试题解析
13. 等腰三角形一腰上的高与另一腰的夹角的度数为20°，则顶角的度数是．

查看试题解析
14. 若a＜ $\sqrt{13}$ ＜b，且a，b为连续正整数，则 $b^{2}$ － $a^{2}$ = ．

查看试题解析
15. 如图， $∠ 1 = ∠ 2$ ，要使 $△ A B E ≌ △ A C E$ ，还需添加一个条件是：.（填上你认为适当的一个条件即可）

查看试题解析
16. 在直线上按照如图所示方式放置面积为S₁、S₂、.S₃的正方形.若S₁=1、 S₂=3，则S₃=.

查看试题解析
17. 如图，在△ABC中，∠ACB=90°，AB=10，AC=8，P是AB边上的动点（不与点B重合），点B关于直线CP的对称点是B′，连接B′A，则B′A长度的最小值是.

查看试题解析

三、解答题

18.

(1)、计算： ${(π - 3.14)}^{0} + \sqrt{5} - | 2 - \sqrt{5} | - {(\sqrt{5})}^{2}$ ；

(2)、求 $x$ 的值： ${(2 x - 1)}^{3} - 8 = 0$

查看试题解析
19. 已知 $\sqrt{x - y + 3}$ 与 $\sqrt{x + y - 1}$ 互为相反数，求 ${(x^{2} - y^{2})}^{2}$ 的平方根.

查看试题解析
20. 如图，△ABC中，AB＝AC，AB的垂直平分线DE分别交AC、AB于点D、E.

(1)、若∠A＝50°，求∠CBD的度数；

(2)、若AB＝8，△CBD周长为13，求BC的长.

查看试题解析
21. 如图，一木杆在离地某处断裂，木杆顶部落在离木杆底部12米处，已知木杆原长18米，求木杆断裂处离地面多少米？

查看试题解析
22. 如图所示，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点．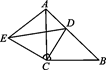

(1)、求证：△ACE≌△BCD；

(2)、若AD＝5，BD＝12，求DE的长．

查看试题解析
23. 如图是规格为8×8的正方形网格，每个小方格都是边长为1的正方形.

( 1 )在网格中建立平面直角坐标系，使A点坐标为(﹣2，4)；

( 2 )在第二象限内的格点(网格线的交点)上画一点C，使点C与线段AB组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是_▲_.

( 3 )画出△ABC关于y轴对称的△A′B′C′.

查看试题解析
24. 如图，在平面直角坐标系中长方形ABCO的顶点A，C的坐标分别为(0，8) ，(20，0)，D是OC的中点，点P在AB上运动，当△ODP是腰长为10的等腰三角形时，求点P的坐标.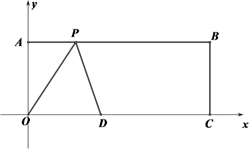

查看试题解析
25. 如图

(1)、（方法引领）如图1，点E、F分别是正方形ABCD的BC、CD边上的动点，连接AE、AF和EF，∠EAF=45°.若BE=2，DF=3，求EF的长.
聪聪同学的思路是：如图2，将△ABE绕点A逆时针旋转90°，证明△AEF≌△AE’F从而得到EF=E’F.请你帮助聪聪同学完成解题过程.

(2)、（灵活应用）如图3，Rt△ABC中，∠ ACB=90°， AC=BC.点D、E在边AB上，且∠DCE=45°.若AD=2，BE=3，求DE的长.

(3)、（拓展提升）如图4，△ABC中∠BAC=45°，AD⊥BC于点D.若CD=2 ，BD=3，请直接写出△ABC的面积.

查看试题解析