江苏省南通市海门中南东州国际2020-2021学年八年级上学期数学12月月考试卷
试卷更新日期:2021-10-09 类型:月考试卷
一、单选题
-
1. 2019年被称为中国的5G元年,如果运用5G技术,下载一个2.4M的短视频大约只需要0.000048秒,将数字0.000048用科学记数法表示应为( )A、 0.48×10﹣4 B、4.8×10﹣5 C、4.8×10﹣4 D、48×10﹣62. 下列计算正确的是( )A、 B、 C、 D、3. 若代数式 有意义,则x的取值范围是( )A、x≠-5 B、x≥﹣ 且x≠-5 C、x≠-5且x≠ D、x≥﹣4. 在下列因式分解的过程中,分解因式正确的是( )A、 B、 C、 D、5. 如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE ≌△ACD的是( )
 A、∠B=∠C B、AD=AE C、∠BDC=∠CEB D、BE=CD6. 有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示.右边场地为长方形,长为 ,则宽为( )
A、∠B=∠C B、AD=AE C、∠BDC=∠CEB D、BE=CD6. 有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示.右边场地为长方形,长为 ,则宽为( ) A、 B、1 C、 D、a+b7. 如图,经过直线AB外一点C作这条直线的垂线,作法如下:
A、 B、1 C、 D、a+b7. 如图,经过直线AB外一点C作这条直线的垂线,作法如下:
(1)任意取一点K , 使点K和点C在AB的两旁.(2)以点C为圆心,CK长为半径作弧,交AB于点D和E . (3)分别以点D和点E为圆心,大于 的长为半径作弧,两弧相交于点F . (4)作直线CF . 则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为( ) A、△CDF B、△CDK C、△CDE D、△DEF8. △ABC中,AB=3,AC=2,BC=a,下列数轴中表示的a的取值范围,正确的是( )A、
A、△CDF B、△CDK C、△CDE D、△DEF8. △ABC中,AB=3,AC=2,BC=a,下列数轴中表示的a的取值范围,正确的是( )A、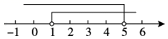 B、
B、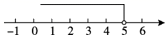 C、
C、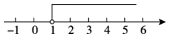 D、
D、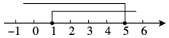 9. 若 ,其中 ,以下分式中一定比 大的是( )A、 B、 C、 D、10. 已知 ,且 > >0,则 的值为( )A、3 B、±3 C、2 D、±211. 如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长( )
9. 若 ,其中 ,以下分式中一定比 大的是( )A、 B、 C、 D、10. 已知 ,且 > >0,则 的值为( )A、3 B、±3 C、2 D、±211. 如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长( )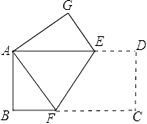 A、3 B、4 C、3.5 D、612. 已知锐角△ABC的三边长恰为三个连续整数,AB>BC>CA,若边BC上的高为AD,则BD﹣DC=( )A、3 B、4 C、5 D、6
A、3 B、4 C、3.5 D、612. 已知锐角△ABC的三边长恰为三个连续整数,AB>BC>CA,若边BC上的高为AD,则BD﹣DC=( )A、3 B、4 C、5 D、6二、填空题
-
13. 点M(3,﹣4)关于x轴的对称点的坐标是 .14. 已知 -2是关于x的分式方程 的根,则实数k的值为 .15. 若 ,则 的值为.16. 如图,平面直角坐标系 中,点A(4,3),点B(3,0),点C(5,3), 沿AC方向平移AC长度的到 ,四边形ABFC的面积为.
 17. 在 中,AC=8, ,AB=6,则BC=.18. 如图,∠ABC=60°,AB=3,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,设点P的运动时间为t秒,当△ABP是钝角三角形时,t满足的条件是.
17. 在 中,AC=8, ,AB=6,则BC=.18. 如图,∠ABC=60°,AB=3,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,设点P的运动时间为t秒,当△ABP是钝角三角形时,t满足的条件是.
三、解答题
-
19.(1)、计算:(2)、因式分解:20. 先化简,再求值:(1+ )÷ ,其中x= ﹣2.21. 决定利用业余时间练习打字,经测试现在小明打140个字所用时间与小海打175个字所用时间相同,小明平均每分钟比小海少打15个字.请求出小明平均每分钟打字的个数.22. 如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE.
 (1)、试说明△BDE≌△CDF;(2)、请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.23. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(1,4),(0,1).
(1)、试说明△BDE≌△CDF;(2)、请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.23. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(1,4),(0,1).
⑴请做出 关于y轴对称的 ,并写出点 的坐标;
⑵使用不带刻度的直尺画出线段EF(E,F均为格点),使得EF经过 一边的中点(画出一条即可)
24. 如图,△ABC中,AB=6cm,AC=4 cm,BC=2 cm,点P以1cm/s的速度从点B出发沿边BA→AC运动到点C停止,运动时间为ts,点Q是线段BP的中点. (1)、若CP⊥AB时,求t的值;(2)、若△BCQ是直角三角形时,求t的值;25. 对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
(1)、若CP⊥AB时,求t的值;(2)、若△BCQ是直角三角形时,求t的值;25. 对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
 (1)、如图1,点A,B的坐标分别为(-2,0),(2,0),则在 , , , 中,线段AB的“近轴点”是.(2)、如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
(1)、如图1,点A,B的坐标分别为(-2,0),(2,0),则在 , , , 中,线段AB的“近轴点”是.(2)、如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ▲ ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.
26. 初识模型:如果两个等腰三角形顶角相等,且顶角顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四边形,形象的可以看作两双手,所以通常称为“手拉手全等模型”.如图1,已知 与 都是等腰三角形, ,且 ,显然 .

 (1)、理解模型:如图2,在 中, ,连接AD,若 ,求AD.(2)、运用模型:如图3,已知 ,AB=AC,点G为BC上一点,点D为BC中点, 于点E, 于点F,判断 的数量关系,并说明理由.(3)、迁移模型:如图3,等边 的边长为6,D是BC的中点,E是AC边上的一点, 内部作等边三角形DEF,若 ,直接写出线段CE的长.
(1)、理解模型:如图2,在 中, ,连接AD,若 ,求AD.(2)、运用模型:如图3,已知 ,AB=AC,点G为BC上一点,点D为BC中点, 于点E, 于点F,判断 的数量关系,并说明理由.(3)、迁移模型:如图3,等边 的边长为6,D是BC的中点,E是AC边上的一点, 内部作等边三角形DEF,若 ,直接写出线段CE的长.