备考2022年中考数学一轮复习（湘教版）专题55 图形变换的简单应用

试卷更新日期：2021-10-09 类型：一轮复习

进入出卷网下载

一、单选题

1. 若点 $A$ 的坐标为 $(6 ， 3)$ ， $O$ 为坐标原点，将 $O A$ 绕点 $O$ 按顺时针方向旋转 $90 °$ 得到 $O A^{'}$ ，则点 $A^{'}$ 的坐标是（）

A、 $(3 ， - 6)$ B、 $(- 3 ， 6)$ C、 $(- 3 ， - 6)$ D、 $(3 ， 6)$

查看试题解析
2. 如图，在扇形 $B O C$ 中， $∠ B O C = 60 °$ ，点 $D$ 是 $\overset{⌢}{B C}$ 的中点，点 $E$ 、 $F$ 分别为半径 $O C$ ， $O B$ 上的动点．若 $O B = 2$ ，则 $△ D E F$ 周长的最小值为（）

A、2 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{3}$

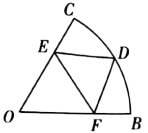查看试题解析
3. 有一正方形卡纸，如图①，沿虚线向上翻折，得到图②，再沿虚线向右翻折得到图③，沿虚线将一角剪掉后展开，得到的图形是（）

A、 B、 C、 D、

查看试题解析
4. 如图，将矩形纸片ABCD沿对角线BD折叠，点C落在点E处，BE与AD相交于点F ， ∠EDF＝42°，则∠DBE的度数是（　　）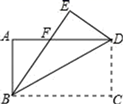

A、21° B、23° C、24° D、42°

查看试题解析
5. 一张正方形纸片按图1，图2对折后，再按图3打出一个半圆形小孔，则展开铺平后的图案是（）

A、 B、 C、 D、

查看试题解析
6. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成轴对称图形，该小正方形的序号是（）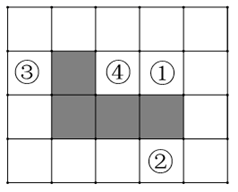

A、① B、② C、③ D、④

查看试题解析
7. 如图，在锐角△ABC中，AB＝6，∠ABC＝60°，∠ABC的平分线交AC于点D，点P，Q分别是BD，AB上的动点，则AP＋PQ的最小值为（）

A、6 B、6 $\sqrt{3}$ C、3 D、3 $\sqrt{3}$

查看试题解析
8. 如图， $A D$ 为 $△ A B C$ 的中线，将 $△ A B D$ 沿着 $A D$ 翻折得到 $△ A E D$ ，点B的对应点为E ， $A E$ 与 $B C$ 相交于点F ，连接 $C E$ ，则下列结论一定正确的是（）

A、 $D F = F C$ B、 $A E ⊥ B C$ C、 $∠ D E C = ∠ D C E$ D、 $∠ B A D = ∠ C A E$

查看试题解析
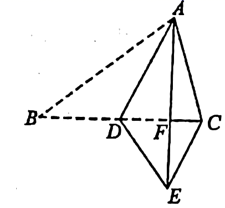9. 如图，把一个长方形纸片对折两次，然后沿图中虚线剪下一个角，若打开后得到一个正方形纸片，剪切线与折痕所成的角的大小等于（）

A、90° B、60° C、45° D、30°

查看试题解析
10. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，AB的中点为D.以C为原点，射线CB为x轴的正方向，射线CA为y轴的正方向建立平面直角坐标系.P是BC上的一个动点，连接AP、DP，则AP+DP最小时，点P的坐标为（）

A、（ $\frac{2}{3}$ ，0） B、（ $\frac{\sqrt{2}}{2}$ ，0） C、（ $\frac{\sqrt{10}}{10}$ ，0） D、（ $\frac{1}{10}$ ，0）

查看试题解析

二、填空题

11. 如图， $⊙ O$ 的直径 $C D$ 为6 $cm$ ， $O A$ ， $O B$ 都是 $⊙ O$ 的半径， $∠ A O D = 2 ∠ A O B = 60 °$ ，点P在直径 $C D$ 上移动，则 $A P + B P$ 的最小值为．

查看试题解析
12. 在平面直角坐标系中，点A的坐标为 $(2 ， 5)$ ，点B的坐标为 $(4 ， 1)$ ，点C、D分别为坐标轴x轴和y轴上的任意一点，则四边形 $A B C D$ 的周长的最小值为．

查看试题解析
13. 如图，在三角形纸片ABC中，已知∠ABC＝90°，AB＝6，BC＝8.过点A作直线平行于BC，折叠三角形纸片ABC，使直角顶点B落在直线 $l$ 上的点T处，折痕为MN，当点T在直线 $l$ 上移动时，折痕的端点M，N也随之移动.若限定端点M，N分别在AB，BC边上移动（点M可以与点A重合，点N可以与点C重合），则线段AT长度的最大值与最小值的和为（计算结果不取近似值）.

查看试题解析
14. 如图，在每个小正方形的边长为1的网格中，A ， B ， C均为格点．

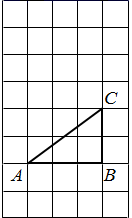(1)、 $△ A B C$ 的边 $A C$ 的长等于；

(2)、点P ， Q分别为边 $A B$ 、 $A C$ 上的动点，连接 $P Q$ 、 $Q B$ ，当 $P Q + Q B$ 取得最小值时，请在如图所示的网格中，用无刻度的直尺画出点P ， Q的位置，并简要说明是如何找到的（不要求证明）．

查看试题解析
15. 如图，平面直角坐标系中，已知 $△ A B C$ 三个顶点的坐标分别为 $A (0 ， 4)$ ， $B (- 1 ， 0)$ ， $C (- 4 ， 2)$ ，将 $△ A B C$ 沿x轴折叠得到 $△ A_{1} B C_{1}$ ，再将 $△ A_{1} B C_{1}$ 绕原点O逆时针旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，则点 $C_{1}$ 的对应点 $C_{2}$ 的坐标为.

查看试题解析
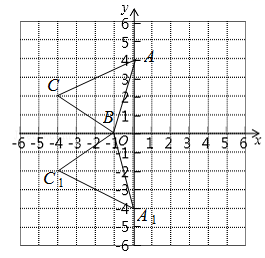16. 如图，已知△ABC为等腰直角三角形，AC＝BC＝6，∠BCD＝15°，P为直线CD上的动点，则|PA－PB|的最大值为.

查看试题解析
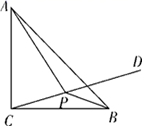17. 如图，正方形ABCD的边长为8，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是．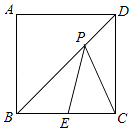

查看试题解析

三、作图题

18. 如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A（﹣1，4），B（﹣3，1）.

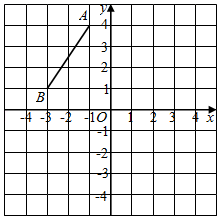
（ 1 ）画出线段AB向右平移4个单位后的线段A₁B₁；

（ 2 ）画出线段AB绕原点O旋转180°后的线段A₂B₂.

查看试题解析
19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后， $△ A B C$ 的顶点均在格点上.

（ 1 ）画出 $△ A B C$ 关于原点对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

（ 2 ）画出 $△ A B C$ 向上平移4个单位后的 $△ A_{2} B_{2} C_{2}$ ，并求平移过程中 $△ A B C$ 扫过的面积.

查看试题解析
20. 如图，方格纸上每个小正方形的边长均为1个单位长度，点A、B都在格点上（两条网格线的交点叫格点）.

（ 1 ）将线段AB向上平移两个单位长度，点A的对应点为点 $A_{1}$ ，点B的对应点为点 $B_{1}$ ，请画出平移后的线段 $A_{1} B_{1}$ ；

（ 2 ）将线段 $A_{1} B_{1}$ 绕点 $A_{1}$ 按逆时针方向旋转 $90^{°}$ ，点 $B_{1}$ 的对应点为点 $B_{2}$ ，请画出旋转后的线段 $A_{1} B_{2}$ ；

（ 3 ）连接 $A B_{2}$ 、 $B B_{2}$ ，求 $Δ A B B_{2}$ 的面积.

查看试题解析
21. 如图，在边长为1个单位长度的小正方形组成的 $10 \times 10$ 的网格中，已知点O，A，B，C均为网格线的交点．

(1)、将 $△ A B C$ 向右平移4个单位，再向上平移3个单位得到 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ （点 $A_{1} ， B_{1} ， C_{1}$ 分别为A，B，C的对应点）

(2)、以点O为旋转中心将 $△ A_{1} B_{1} C_{1}$ 逆时针旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，请画出 $△ A_{2} B_{2} C_{2}$ ；并写出在旋转过程中点 $A_{1}$ 到 $A_{2}$ 所经过的路径长为．（点 $A_{2} ， B_{2} ， C_{2}$ 分别为 $A_{1} ， B_{1} ， C_{1}$ 的对应点）

查看试题解析
22. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点四边形 $A B C D$ （顶点是网格线的交点）和格点 $O$ ．

（ 1 ）把四边形 $A B C D$ 平移，使得顶点 $C$ 与 $O$ 重合，画出平移后得到的四边形 $A_{2} B_{1} C_{1} D_{1}$ ；

（ 2 ）把四边形 $A B C D$ 绕 $O$ 点顺时针旋转90°，画出旋转后得到的四边形 $A_{2} B_{2} C_{2} D_{2}$ ．

查看试题解析

四、解答题

23. 在如图所示的网格中建立平面直角坐标系， $△ A B C$ 的顶点在网格线的交点上，点 $B$ 的坐标为 $(- 1 ， - 1)$ ．

(1)、画出 $△ A B C$ 向上平移4个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $B$ 的对应点 $B_{1}$ 的坐标；

(2)、画出 $△ A_{1} B_{1} C_{1}$ 绕原点 $O$ 顺时针旋转90°得到的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $B_{1}$ 的对应点 $B_{2}$ 的坐标．

查看试题解析
24. 如图

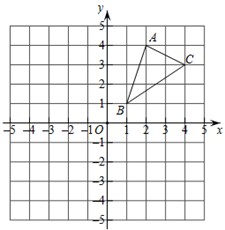
（1）请画出△ABC关于原点O对称的△A₁B₁C₁；
（2）请画出△ABC绕点B逆时针旋转90°后的△A₂BC₂；
（3）写出A₂和C₂两点坐标．

查看试题解析
25. 如图，方格纸中的每个小正方形边长都是1个长度单位，Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（1，1），点B的坐标为（4，1）．
①先将Rt△ABC向左平移5个单位长度，再向下平移1个单位长度得到Rt△A₁B₁C₁ ，试在图中画出Rt△A₁B₁C₁ ，并写出点B₁的坐标；
②再将Rt△A₁B₁C₁绕点A₁顺时针旋转90°后得到Rt△A₂B₂C₂ ，试在图中画出Rt△A₂B₂C₂ ．并写出点B₂的坐标．

查看试题解析

五、综合题

26. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（﹣1，3），B（﹣4，0），C（0，0）

(1)、画出将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A₁B₁C₁；

(2)、画出将△ABC绕原点O顺时针方向旋转90°得到△A₂B₂O；

(3)、在x轴上存在一点P，满足点P到A₁与点A₂距离之和最小，请直接写出P点的坐标．

查看试题解析
27. 如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣4，4），B（﹣2，5），C（﹣2，1）．

(1)、①平移△ABC，使点C移到点C₁（﹣2，﹣4），画出平移后的△A₁B₁C₁ ，并写出点A₁ ， B₁的坐标；
②将△ABC绕点（0，3）旋转180°，得到△A₂B₂C₂ ，画出旋转后的△A₂B₂C₂；

(2)、求（1）②中的点C旋转到点C₂时，点C经过的路径长（结果保留π）．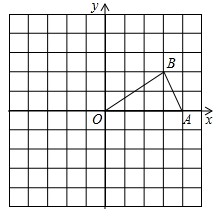

查看试题解析
28. 如图，已知点 $A ， B$ 的坐标分别为 $(4 ， 0)$ ， $(3 ， 2)$ ．

(1)、①画出 $Δ A O B$ 关于原点O对称的图形 $Δ C O D$ （点A对应点C）；
②将 $Δ A O B$ 绕点O按逆时针方向旋转 $90 °$ 得到 $Δ E O F$ （点A对应点E）．画出 $Δ E O F$ ；

(2)、点D的坐标是，点F的坐标是，此图中线段 $B F$ 和 $D F$ 的关系是．

查看试题解析
29. 图①②都是由边长为1的小等边三角形组成的正六边形，已经有5个小等边三角形涂上阴影，请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影.（请将两个小题依次作答在图①，图②中，均只需画出符合条件的一种情形）

(1)、使得6个阴影小等边三角形组成的图形是轴对称图形，但不是中心对称图形.

(2)、使得6个阴影小等边三角形组成的图形既是轴对称图形，又是中心对称图形.

查看试题解析