陕西省渭南市富平县2021届高三下学期理数二模试卷

试卷更新日期：2021-10-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数z满足 $z (1 - i) = 5 + i$ ，其中i为虚数单位，则z的虚部是（）

A、3 B、3i C、2 D、2i

查看试题解析
2. 已知集合 $A = {- 2 ， - 1 ， 0 ， 1 ， 2}$ ， $B = {x | x^{2} \leq 1}$ ，则 $A \cap B$ 的元素个数为（）

A、2 B、3 C、4 D、5

查看试题解析
3. 函数 $f (x) = \frac{x^{3}}{e^{- x} - e^{x}}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
4. 学校组织开展劳动实践，高二某班15名学生利用假期时间前往敬老院､消防队等场所劳动服务.经统计，该15名学生的劳动服务时长平均为20小时，标准差为s后来经核实，发现统计的甲､乙两名同学的劳动服务时长有误.甲同学的劳动服务时长实际为20小时，被误统计为15小时；乙同学的劳动服务时长实际为18小时，被误统计为23小时.更正后重新计算，得到标准差为 $s_{1}$ ，则s与 $s_{1}$ 的大小关系为（）

A、 $s = s_{1}$ B、 $s < s_{1}$ C、 $s > s_{1}$ D、无法判断

查看试题解析
5. 下列函数中，周期为π，且在区间 $(\frac{π}{2} ， π)$ 上单调递增的是（）

A、 $y = \cos 2 x$ B、 $y = \sin 2 x$ C、 $y = \sin x$ D、 $y = \sin | x |$

查看试题解析
6. 设等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $S_{10} = 20$ ， $S_{20} = 30$ ，则 $S_{30} =$ （）

A、20 B、30 C、40 D、50

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的渐近线与圆 $x^{2} + y^{2} - 4 y + 3 = 0$ 相切，则 $a =$ （）

A、3 B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{3}$

查看试题解析
8. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{n} = (3 n - 19) \cdot 5^{n}$ ，则当 $S_{n}$ 取最小值时，n的值为（）

A、5 B、6 C、7 D、8

查看试题解析
9. 近些年，我国在治理生态环境方面推出了很多政策，习总书记明确提出大力推进生态文明建设，努力建设美丽中国!某重型工业企业的生产废水中某重金属对环境有污染，因此该企业研发了治理回收废水中该重金属的过滤装置，废水每通过一次该装置，可回收20%的该重金属.若当废水中该重金属含量低于最原始的5%时，至少需要经过该装置的次数为（）(参考数据： $\lg 2 \approx 0.301$ )

A、11 B、12 C、13 D、14

查看试题解析
10. 已知函数 $f (x) = \log_{3} x$ ，给出三个条件：① $f (a_{n}) = 2^{n}$ ；② $f (a_{n}) = n$ ；③ $f (a_{n}) = \frac{1}{n}$ .从中选出一个能使数列 ${a_{n}}$ 成等比数列的条件，在这个条件下，数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n} =$ （）

A、 $3^{n} - 1$ B、 $2^{n + 1} - 1$ C、 $\frac{1}{2} (3^{n} - 1)$ D、 $\frac{3}{2} (3^{n} - 1)$

查看试题解析
11. 刘徽《九章算术注》记载：“邪解立方有两堑堵，邪解堑堵，其一为阳马，一为鳖臑，阳马居二，鳖臑居一，不易之率也”.意思是：把一长方体沿对角面一分为二，这相同的两块叫做堑堵，沿堑堵的一顶点与其相对的棱剖开成两块，大的叫阳马，小的叫鳖臑，两者体积之比为定值2：1，这一结论今称刘徽原理.如图是一个阳马的三视图，则其外接球的体积为（）

A、4π B、3π C、 $\sqrt{3} π$ D、 $\frac{\sqrt{3}}{2} π$

查看试题解析
12. 若函数 $y = f (x) (x \in R)$ 满足 $f (x + 1) = - f (x)$ ，且 $x \in [- 1 ， 1]$ 时， $f (x) = 1 - x^{2}$ ，已知函数 $g (x) = {\begin{array}{l} | \lg x | ， x > 0 ， \\ e^{x} ， x < 0 ， \end{array}$ 则函数 $h (x) = f (x) - g (x)$ 在区间 $[- 6 ， 6]$ 内的零点个数为（）

A、14 B、13 C、12 D、11

查看试题解析

二、填空题

13. 已知平面向量 $| \vec{a} | = 3$ ， $| \vec{b} | = 2$ ， $\vec{a} \cdot (\vec{a} - \vec{b}) = 8$ ，则 $\cos 〈 \vec{a} ， \vec{b} 〉 =$ .

查看试题解析
14. 2021年是中国共产党百年华诞.某学校社团将举办庆祝中国共产党成立100周年革命歌曲展演.现从《歌唱祖国》､《英雄赞歌》､《唱支山歌给党听》､《毛主席派人来》4首独唱歌曲和《没有共产党就没有新中国》､《我和我的祖国》2首合唱歌曲中共选出4首歌曲安排演出，要求最后一首歌曲必须是合唱，则不同的安排方法共有种.

查看试题解析
15. 已知F是抛物线 $y^{2} = 4 x$ 的焦点，P是抛物线上的一个动点，A（3，1），则 $△ A P F$ 周长的最小值为.

查看试题解析
16. 在空间中，给出下面四个命题，其中真命题的个数为.
①过平面 $α$ 外的两点，有且只有一个平面与平面 $α$ 垂直；

②若平面 $β$ 内有不共线三点到平面 $α$ 的距离都相等，则 $α / / β$ ；

③若直线 $l$ 与平面 $α$ 内的无数条直线垂直，则 $l ⊥ α$ ；

④两条异面直线在同一平面内的射影一定是两条相交直线.

查看试题解析

三、解答题

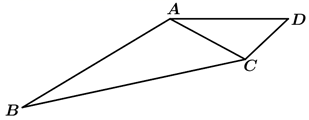17. 如图，在平面四边形ABCD中， $∠ D A B = \frac{5 π}{6}$ ， $∠ A D C = \frac{π}{4}$ ， $A B = 2 A C = 2 \sqrt{2}$ ， $C D = 1$ .

(1)、求 $∠ C A D$ 的大小；

(2)、求BC的长.

查看试题解析
18. 中国探月工程自2004年批准立项以来，聚焦“自主创新､重点跨越､支撑发展､引领未来”的目标，创造了许多项中国首次.2020年12月17日凌晨，嫦娥五号返回器携带“月壤”着陆地球，首次实现了我国地外天体无人采样返回.为了了解某中学高三学生对此新闻事件的关注程度，从该校高三学生中随机抽取了100名学生进行调查，调查样本中有40名女生.如图是根据样本的调查结果绘制的等高条形图（阴影区域表示关注“嫦娥五号”的部分）.

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .

$P (K^{2} ⩾ k_{0})$

0.150

0.100

0.050

0.010

0.005

$k_{0}$

2.072

2.706

3.841

6.635

7.879

(1)、完成下面的列联表，并判断是否有95%的把握认为对“嫦娥五号”的关注程度与性别有关？

关注

没关注

合计

男生

女生

合计

(2)、若将频率视为概率，现从该中学高三女生中随机抽取2人.记被抽取的2名女生中对“嫦娥五号”新闻关注的人数为随机变量X，求X的分布列及数学期望.

查看试题解析
19. 如图，在三棱锥 $A - B C D$ 中， $C D ⊥$ 平面ABC， $A C = C B = \frac{1}{2} C D$ ， $∠ A C B = 90 °$ ，点E，F分别是AB，AD的中点.

(1)、求证： $A C ⊥$ 平面BCD；

(2)、设 $A C = C B = 2$ ，求直线AD与平面CEF所成角的正弦值

查看试题解析
20. 已知点 $P$ 为椭圆 $W ： \frac{2 x^{2}}{m^{2}} + y^{2} = 1$ （ $m > 0$ ）上任一点，椭圆的一个焦点坐标为 $(- \sqrt{2} ， 0)$ ．

(1)、求椭圆的标准方程；

(2)、若点 $Q$ 是抛物线 $C ： x^{2} = 2 m y$ 的准线上的任意一点，以 $P Q$ 为直径的圆过原点 $O$ ，试判断 $\frac{1}{{| O P |}^{2}} + \frac{1}{{| O Q |}^{2}}$ 是否为定值？若是，求出这个定值；若不是，请说明理由．

查看试题解析
21. 已知函数 $f (x) = a \ln x + x (a \neq 0)$ ， $g (x) = e^{x} + b x^{2} (b \in R)$ .

(1)、记 $h (x) = f (x) + x^{2}$ ，试讨论函数 $h (x)$ 的单调性；

(2)、若曲线 $y = f (x)$ 与曲线 $y = g (x)$ 在 $x = 1$ 处的切线都过点（0，1）.求证：当 $x > 0$ 时， $f (x) + \frac{g (x) - 1}{x} \geq e - 1$ .

查看试题解析
22. 以坐标原点为极点， $x$ 轴的正半轴为极轴建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ^{2} + 2 ρ \cos θ - 3 = 0$ ，直线 $l$ 的极坐标方程为 $ρ \sin (θ + \frac{π}{4}) = \sqrt{2}$ .

(1)、求曲线 $C$ ､直线 $l$ 的直角坐标方程；

(2)、若直线 $l^{'}$ 过点 $M (- 2 ， 1)$ 且与直线 $l$ 平行，直线 $l^{'}$ 交曲线 $C$ 于 $A$ ， $B$ 两点，求 $| M A | \cdot | M B |$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x - 2 | + | x - m | ， m > 0$ ，且 $f (x)$ 的最小值为2．

(1)、求m的值；

(2)、若 $a ， b ， c$ 均为正数，且 $a + b + c = m$ ，求证： $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{4}$ ．

查看试题解析

$P (K^{2} ⩾ k_{0})$	0.150	0.100	0.050	0.010	0.005
$k_{0}$	2.072	2.706	3.841	6.635	7.879

	关注	没关注	合计
男生
女生
合计