陕西省部分重点高中2020-2021学年高三上学期理数12月联考试卷
试卷更新日期:2021-10-09 类型:月考试卷
一、单选题
-
1. 设集合 ,则 ( )A、 B、 C、 D、2. 若 ,则( )A、 的实部为1 B、 的实部为-1 C、 的虚部为 D、 的虚部为3. 某地区7月1日至7月10日白天的平均气温的折线图如图所示,则下列判断错误的是( )
 A、从7月2日到7月5日白天的平均气温呈下降趋势 B、这10天白天的平均气温的极差大于6℃ C、这10天中白天的平均气温为26℃的频率最大 D、这10天中白天的平均气温大于26℃的有5天4. 若函数 的图象关于点 对称,则( )A、 为偶函数 B、 为偶函数 C、 为奇函数 D、 为奇函数5. 在平行四边形 中, ,且 .则 ( )A、-5 B、-6 C、5 D、66. 函数 的最小正周期为( )A、 B、 C、 D、7. 若随机变量 的分布列为
A、从7月2日到7月5日白天的平均气温呈下降趋势 B、这10天白天的平均气温的极差大于6℃ C、这10天中白天的平均气温为26℃的频率最大 D、这10天中白天的平均气温大于26℃的有5天4. 若函数 的图象关于点 对称,则( )A、 为偶函数 B、 为偶函数 C、 为奇函数 D、 为奇函数5. 在平行四边形 中, ,且 .则 ( )A、-5 B、-6 C、5 D、66. 函数 的最小正周期为( )A、 B、 C、 D、7. 若随机变量 的分布列为0
10
20
30
0.1
0.3
0.5
0.1
则 ( )
A、16 B、32 C、18 D、648. 在 中, ,且 的面积为 ,则 外接圆的半径的最小值是( )A、 B、6 C、 D、129. 若从1,3,5,7中选取两个数,从0,2,4,6,8中选取两个数,将这四个数组成一个无重复数字的四位数,则不同的四位数的总个数为( )A、1296 B、1320 C、1440 D、152410. 某三棱锥的三视图如图所示,则该三棱锥的体积为( ) A、 B、1 C、 D、211. 已知函数 ,若 对 恒成立,则 的取值范围是( )A、 , B、 C、 , D、12. 已知双曲线C的方程为 ,给出下列四个结论:
A、 B、1 C、 D、211. 已知函数 ,若 对 恒成立,则 的取值范围是( )A、 , B、 C、 , D、12. 已知双曲线C的方程为 ,给出下列四个结论:①m的取值范围是 ;②C的焦距与m的取值无关;③当C的离心率不小于2时,m的最小值为 ;④存在实数m , 使得点 在C上.其中结论正确的个数为( )
A、1 B、2 C、3 D、4二、填空题
-
13. 若 ,则 .14. 椭圆 上一点到两焦点的距离之和为 .15. 若函数 ,则 的值域为.16. 已知底面为矩形的四棱锥 的每个顶点都在球O的球面上, , , ,且 .若球O的体积为 ,则棱 的中点到平面 的距离为.
三、解答题
-
17. 在递增的等比数列 中, , .(1)、求数列 的通项公式;(2)、若 ,求数列 的前 项和 .18. 某公司销售部门对某产品在某地区的广告投入与纯利润之间的关系进行研究,记录了2020年6月份到10月份的广告费与纯利润,得到如下资料表:
月份
6
7
8
9
10
广告费 (万元)
10
11
13
12
9
纯利润 (万元)
23
25
30
26
16
附:回归直线 的斜率和截距的最小二乘估计分别为 , .
(1)、根据6至10月份的数据,求出 关于 的线性回归方程;(2)、该公司销售部门打算11月份对该地区投入广告费15万元,但公司决策部门规定,当纯利润预测不低于35万元时才能对该地区继续投人广告,否则终止投入广告,试判断销售部门对该地区是否继续投入广告.19. 如图,菱形 的对角线 与 交于点 , , ,将 沿 折到 的位置使得 .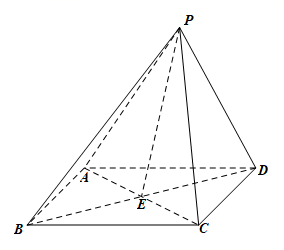 (1)、证明: .(2)、求平面 与平面 所成锐二面角的余弦值.20. 已知抛物线 : ( )的焦点为 ,点 , .(1)、求抛物线 的方程;(2)、已知过点 的直线l交抛物线 于 , 两点,当 到 的距离最大时,求 的面积.
(1)、证明: .(2)、求平面 与平面 所成锐二面角的余弦值.20. 已知抛物线 : ( )的焦点为 ,点 , .(1)、求抛物线 的方程;(2)、已知过点 的直线l交抛物线 于 , 两点,当 到 的距离最大时,求 的面积.