江苏省无锡市八校联盟2020-2021学年高三上学期数学第三次适应性检测试卷
试卷更新日期:2021-10-08 类型:高考模拟
一、单选题
-
1. 若角 的终边经过点 ,则( )A、 B、 C、 D、2. 设函数 的定义域 ,函数 的定义域为 ,则 ( )A、 B、 C、 D、3. 设实数 满足 ,函数 的最小值为( )A、 B、 C、 D、64. 有一个隧道内设双行线公路,其截面由一长方形和抛物线构成,如图所示.为了保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少为0.7m,若行车道总宽度为7.2m,则车辆通过隧道时的限制高度为( )
 A、3.3m B、3.5m C、3.8m D、4.5m5. 函数f(x)= 在[- , ]。的图像大致为( )A、
A、3.3m B、3.5m C、3.8m D、4.5m5. 函数f(x)= 在[- , ]。的图像大致为( )A、 B、
B、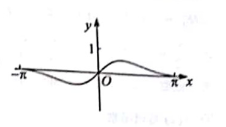 C、
C、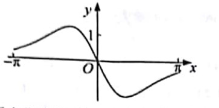 D、
D、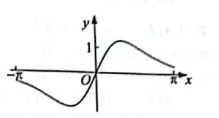 6. 若函数 同时满足:①定义域内存在实数 ,使得 ;②对于定义域内任意 , ,当 时,恒有 ;则称函数 为“ 函数”.下列函数中是“ 函数”的为( )A、 B、 C、 D、7. 已知等差数列 的公差为2,前n项和为 ,且 , , 成等比数列.令 ,数列 的前n项和为 ,若对于 ,不等式 恒成立,则实数 的取值范围是( )A、 B、 C、 D、8. 若椭圆 上的点 到右准线的距离为 ,过点 的直线 与 交于两点 ,且 ,则 的斜率为( )A、 B、 C、 D、
6. 若函数 同时满足:①定义域内存在实数 ,使得 ;②对于定义域内任意 , ,当 时,恒有 ;则称函数 为“ 函数”.下列函数中是“ 函数”的为( )A、 B、 C、 D、7. 已知等差数列 的公差为2,前n项和为 ,且 , , 成等比数列.令 ,数列 的前n项和为 ,若对于 ,不等式 恒成立,则实数 的取值范围是( )A、 B、 C、 D、8. 若椭圆 上的点 到右准线的距离为 ,过点 的直线 与 交于两点 ,且 ,则 的斜率为( )A、 B、 C、 D、二、多选题
-
9. 如图,已知 为正方体,E,F分别是BC, 的中点,则( )
 A、 B、 C、向量 与向量 的夹角是 D、异面直线 与 所成的角为10. 我们把离心率为 的椭圆称为黄金椭圆,类似地,也把离心率为 的双曲线称为黄金双曲线,则( )A、曲线 是黄金双曲线 B、如果双曲线 是黄金双曲线,那么 (c为半焦距) C、如果双曲线 是黄金双曲线,那么右焦点 到一条渐近线的距离等于焦距的四分之一 D、过双曲线 的右焦点 且垂直于实轴的直线l交C于M、N两点,O为坐标原点,若 ,则双曲线C是黄金双曲线11. 已知 ,则( )A、 的值为2 B、 的值为16 C、 的值为﹣5 D、 的值为12012. 对于定义在 上的函数 ,若存在正实数 , ,使得 对一切 均成立,则称 是“控制增长函数”.在以下四个函数中是“控制增长函数”的有( )A、 B、 C、 D、
A、 B、 C、向量 与向量 的夹角是 D、异面直线 与 所成的角为10. 我们把离心率为 的椭圆称为黄金椭圆,类似地,也把离心率为 的双曲线称为黄金双曲线,则( )A、曲线 是黄金双曲线 B、如果双曲线 是黄金双曲线,那么 (c为半焦距) C、如果双曲线 是黄金双曲线,那么右焦点 到一条渐近线的距离等于焦距的四分之一 D、过双曲线 的右焦点 且垂直于实轴的直线l交C于M、N两点,O为坐标原点,若 ,则双曲线C是黄金双曲线11. 已知 ,则( )A、 的值为2 B、 的值为16 C、 的值为﹣5 D、 的值为12012. 对于定义在 上的函数 ,若存在正实数 , ,使得 对一切 均成立,则称 是“控制增长函数”.在以下四个函数中是“控制增长函数”的有( )A、 B、 C、 D、三、填空题
-
13. 被誉为“数学之神”之称的阿基米德(前287—前212),是古希腊伟大的物理学家、数学家、天文学家,他最早利用逼近的思想证明了如下结论:抛物线的弦与抛物线所围成的封闭图形的面积,等于抛物线的弦与经过弦的端点的两条切线所围成的三角形面积的三分之二.这个结论就是著名的阿基米德定理,其中的三角形被称为阿基米德三角形.在平面直角坐标系心中,已知直线l:y=4与抛物线C: 交于A , B两点,则弦与拋物线C所围成的封闭图形的面积为 .14. 地震震级是根据地震仪记录的地震波振幅来测定的,一般采用里氏震级标准.震级 是用据震中100千米处的标准地震仪所记录的地震波最大振幅值的对数来表示的.里氏震级的计算公式为 ,其中 是被测地震的最大振幅, 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).根据该公式可知,7.5级地震的最大振幅是6级地震的最大振幅的倍(精确到1).15. 若不等式 对一切x R恒成立,其中a , b R , e为自然对数的底数,则a+b的取值范围是 .16. 将正奇数按如图所示的规律排列:
1
3 5 7
9 11 13 15 17
19 21 23 25 27 29 31
………………………
则2021在第行,从左向右第个数.
四、解答题
-
17. 在① csinA=acosC;②tan =2+ ;③a2+b2=c2+ ab这三个条件中任选一个,补充在下面问题中,并加以解答.
已知△ABC中的内角A,B,C的对边分别为a,b,c,面积为S,若c=4,B=105°, ▲ , 求a和S.
18. 已知数列 的前n项和为 ,且 , ,n .(1)、求数列 , 的通项公式;(2)、设 ,数列 的前n项和为 ,求证: ≤ < .19. 2019年4月,江苏省发布了高考综合改革实施方案,试行“ ”高考新模式.为调研新高考模式下,某校学生选择物理或历史与性别是否有关,统计了该校高三年级800名学生的选科情况,部分数据如下表:性别
科目
男生
女生
合计
物理
300
历史
150
合计
400
800
附:
0.050
0.010
0.001
k
3.841
6.635
10.828
(1)、根据所给数据完成上述表格,并判断是否有99.9%的把握认为该校学生选择物理或历史与性别有关;(2)、该校为了提高选择历史科目学生的数学学习兴趣,用分层抽样的方法从该类学生中抽取5人,组成数学学习小组.一段时间后,从该小组中抽取3人汇报数学学习心得.记3人中男生人数为X,求X的分布列和数学期望 .20. 如图,在正六边形 中,将 沿直线 翻折至 ,使得平面 平面 ,O,H分别为 和 的中点.
 (1)、证明: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.21. 对于定义在D上的函数f(x),如果存在实数x0 , 使得f(x0)=x0 , 那么称x0是函数f(x)的一个不动点.已知f(x)=ax2+1.(1)、当a=-2时,求f(x)的不动点;(2)、若函数f(x)有两个不动点x1 , x2 , 且x1<2<x2.
(1)、证明: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.21. 对于定义在D上的函数f(x),如果存在实数x0 , 使得f(x0)=x0 , 那么称x0是函数f(x)的一个不动点.已知f(x)=ax2+1.(1)、当a=-2时,求f(x)的不动点;(2)、若函数f(x)有两个不动点x1 , x2 , 且x1<2<x2.①求实数a的取值范围;
②设g(x)=loga[f(x)-x],求证:g(x)在(a,+∞)上至少有两个不动点.
22. 已知O为坐标原点,椭圆C: ,点D,M,N为C上的动点,O,M,N三点共线,直线DM,DN的斜率分别为 , ( ).(1)、证明: ;(2)、当直线DM过点 时,求 的最小值;(3)、若 ,证明: 为定值.