江苏省苏州市张家港市2020-2021学年高三上学期数学12月阶段性调研测试试卷
试卷更新日期:2021-10-08 类型:高考模拟
一、单选题
-
1. 集合 ,集合 ,则 ( )A、 B、 C、 D、2. 复数的 模为( )A、 B、 C、 D、23. 南北朝时期的伟大数学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”.其含义是夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为 、 ,被平行于这两个平面的任意平面截得的两个截面面积分别为 、 ,则命题 :“ 、 相等”是命题 “ 、 总相等”的( )
 A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数 的图象可能是( )A、
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 函数 的图象可能是( )A、 B、
B、 C、
C、 D、
D、 5. 十二平均律是我国明代音乐埋论家和数学家朱载填发明的.明万历十二年(公元1584年),他写成《律学新说》,提出了十二平均律的理论.十二平均律的数学意义是:在1和2之间插入11个正数,使包含1和2的这13个数依次成递增的等比数列.依此规则,插入的第四个数应为( )A、 B、 C、 D、6. 2020年3月9日,我国在西昌卫星发射中心用长征三号运载火箭,成功发射北斗系统第54颗导航卫星.第54颗导航卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为R , 若其近地点、远地点离地面的距离大约分别是 , 则第54颗导航卫星运行轨道(椭圆)的离心率是( )A、 B、 C、 D、7. 定义在 上的偶函数 在 上是增函数,且 ,则不等式 的解集是( )A、 B、 C、 D、8. 在 中, 为边 上的点,且 ,满足则 ( )A、有最小值 B、有最小值 C、有最小值12 D、有最小值16
5. 十二平均律是我国明代音乐埋论家和数学家朱载填发明的.明万历十二年(公元1584年),他写成《律学新说》,提出了十二平均律的理论.十二平均律的数学意义是:在1和2之间插入11个正数,使包含1和2的这13个数依次成递增的等比数列.依此规则,插入的第四个数应为( )A、 B、 C、 D、6. 2020年3月9日,我国在西昌卫星发射中心用长征三号运载火箭,成功发射北斗系统第54颗导航卫星.第54颗导航卫星的运行轨道是以地心为一个焦点的椭圆.设地球半径为R , 若其近地点、远地点离地面的距离大约分别是 , 则第54颗导航卫星运行轨道(椭圆)的离心率是( )A、 B、 C、 D、7. 定义在 上的偶函数 在 上是增函数,且 ,则不等式 的解集是( )A、 B、 C、 D、8. 在 中, 为边 上的点,且 ,满足则 ( )A、有最小值 B、有最小值 C、有最小值12 D、有最小值16二、多选题
-
9. 已知函数 (其中 )的部分图象如图所示,则下列结论正确的是( )
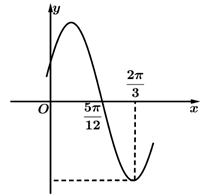 A、函数 的图象关于直线 对称 B、函数 的图象关于点 对称 C、函数 在区间 上单调增 D、函数 的图象可由 的图象向左平移 个单位得到10. 下列不等关系正确的是( )A、 B、若 , ,则 C、当 时 D、11. 如图,正方体 的棱长为1,点 是侧面 的一个动点,则下列结论正确的是( )
A、函数 的图象关于直线 对称 B、函数 的图象关于点 对称 C、函数 在区间 上单调增 D、函数 的图象可由 的图象向左平移 个单位得到10. 下列不等关系正确的是( )A、 B、若 , ,则 C、当 时 D、11. 如图,正方体 的棱长为1,点 是侧面 的一个动点,则下列结论正确的是( ) A、点 存在无数个位置满足 B、点 存在无数个位置满足到直线 和直线 的距离相等 C、三棱锥 的体积最大值为 D、在线段 上存在点 ,使异面直线 与 所成的角也是12. 下列命题正确的是( )A、若 是锐角,则 B、若 都是锐角,则 C、若 都是锐角,且 ,则 D、若 都是任意角,且 ,则 的最大值为
A、点 存在无数个位置满足 B、点 存在无数个位置满足到直线 和直线 的距离相等 C、三棱锥 的体积最大值为 D、在线段 上存在点 ,使异面直线 与 所成的角也是12. 下列命题正确的是( )A、若 是锐角,则 B、若 都是锐角,则 C、若 都是锐角,且 ,则 D、若 都是任意角,且 ,则 的最大值为三、填空题
-
13. 已知双曲线 的离心率为 ,则点 到双曲线 的渐近线的距离为. .14. 在等差数列 中, , ,记 ,则数列 的最大项是第项.15. 我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童,如图的刍童 有外接球,且 ,点 到平面 距离为4,则该刍童外接球的表面积为.
 16. 在平面直角坐标系 中,点 在直线 上,点 在圆 上,若四边形 正方形,则 ;若 为直角,则实数 的取值范围的.
16. 在平面直角坐标系 中,点 在直线 上,点 在圆 上,若四边形 正方形,则 ;若 为直角,则实数 的取值范围的.四、解答题
-
17.
① ;② ;③ ;这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求 的最大值.若问题中的三角形不存在,说明理由.
问题:是否存在 ,它的内角其 的对边分别为 ,且, ?
注:如果选择多个条件分别解答,按第一个解答计分.
18. 如图,函数 的图象由曲线段OA和直线段 构成. (1)、写出函数 的解析式;(2)、函数 有零点,求实数 的取值范围.19. 已知正项等比数列 的首项为1,且前三项的和为13.数列 的首项为1,前 项和为 ,且 .(1)、求等比数列 的通项公式;(2)、求证:数列 为等差数列;(3)、若数列 的公差为2,数列 的前 项和为 ,求证: .20. 如图,四棱锥 的底而是边长为2的正方形,平面 底而 ,记平面 平面 .
(1)、写出函数 的解析式;(2)、函数 有零点,求实数 的取值范围.19. 已知正项等比数列 的首项为1,且前三项的和为13.数列 的首项为1,前 项和为 ,且 .(1)、求等比数列 的通项公式;(2)、求证:数列 为等差数列;(3)、若数列 的公差为2,数列 的前 项和为 ,求证: .20. 如图,四棱锥 的底而是边长为2的正方形,平面 底而 ,记平面 平面 . (1)、求证: ;(2)、若 ,求平面 与平面 所成的锐二面角的大小.
(1)、求证: ;(2)、若 ,求平面 与平面 所成的锐二面角的大小.
