北师版数学八年级上册《第三章 位置与坐标》单元检测A卷
试卷更新日期:2021-10-07 类型:单元试卷
一、单选题
-
1. 在平面直角坐标系中,点 关于y轴的对称点的坐标是( )A、 B、 C、 D、2. 在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是( )A、 B、 C、 D、3. 已知点 在 轴上,则点 的坐标是( )A、 B、 C、 D、4. 星城长沙是湖南省省会城市,也是长江中游地区重要的中心城市,以下能准确表示长沙地理位置的是( )A、在北京的西南方 B、东经112.59°,北纬28.12° C、距离北京1478千米处 D、东经112.59°5. 如图所示是雷达探测到的6个目标,若目标B用(30,60°)表示,目标D用(50,210°)表示,则表示为(40,120°)的目标是( )
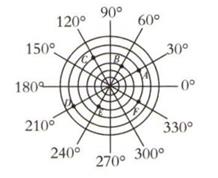 A、目标A B、目标C C、目标E D、目标F6. 如图所示,在方格纸上摆出了六枚棋子,如果用(2,-1)表示棋子A,用(6,-2)表示棋子B,那么(5,3)表示的是( )
A、目标A B、目标C C、目标E D、目标F6. 如图所示,在方格纸上摆出了六枚棋子,如果用(2,-1)表示棋子A,用(6,-2)表示棋子B,那么(5,3)表示的是( )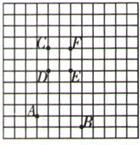 A、棋子E B、棋子D C、棋子C D、棋子F7. 如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )
A、棋子E B、棋子D C、棋子C D、棋子F7. 如图是雷达屏幕在一次探测中发现的多个目标,其中对目标A的位置表述正确的是( )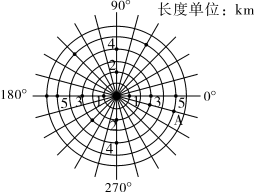 A、在南偏东75°方向处 B、在5km处 C、在南偏东15°方向5km处 D、在南偏东75°方向5km处8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 如图,A(8,0),C(﹣2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
A、在南偏东75°方向处 B、在5km处 C、在南偏东15°方向5km处 D、在南偏东75°方向5km处8. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、Z(﹣1,2)9. 如图,A(8,0),C(﹣2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )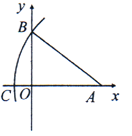 A、(0,5) B、(5,0) C、(6,0) D、(0,6)10. 平面直角坐标系内与点 关于原点对称的点的坐标是( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
A、(0,5) B、(5,0) C、(6,0) D、(0,6)10. 平面直角坐标系内与点 关于原点对称的点的坐标是( )A、 B、 C、 D、11. 如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )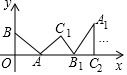 A、 B、 C、 D、12. 将△ABC的三个顶点坐标的横坐标都乘-1,并保持纵坐标不变,则所得图形与原图形的关系是( )
A、 B、 C、 D、12. 将△ABC的三个顶点坐标的横坐标都乘-1,并保持纵坐标不变,则所得图形与原图形的关系是( )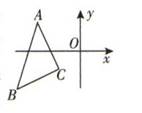 A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将原图形沿x轴的负方向平移了1个单位
A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将原图形沿x轴的负方向平移了1个单位二、填空题
-
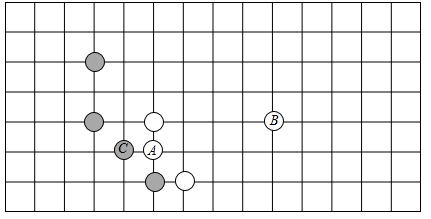
13. 已知Q(2x﹣4,x2﹣1)在x轴上,则点Q的坐标为 .14. 已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为 .
 15. △ABC在如图所示的直角坐标系中,写出△ABC关于y轴对称的△A'B'C'中点A,B关于y轴的对称点A',B'的坐标分别是
15. △ABC在如图所示的直角坐标系中,写出△ABC关于y轴对称的△A'B'C'中点A,B关于y轴的对称点A',B'的坐标分别是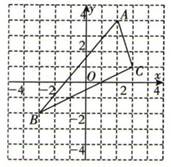 16. 如图所示,点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,则a+b=
16. 如图所示,点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,则a+b= 17. 如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,An(n+1,n),构成形如
17. 如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4),…,An(n+1,n),构成形如 ”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=.
”的图形的阴影部分面积分别表示为S1 , S2 , S3 , …,Sn , 则S2021=. 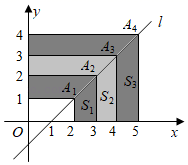 18. 如图,在平面直角坐标系中, 轴,垂足为 ,将 绕点 逆时针旋转到 的位置,使点 的对应点 落在直线 上,再将 绕点 逆时针旋转到 的位置,使点 的对应点 也落在直线 上,以此进行下去……若点 的坐标为 ,则点 的纵坐标为.
18. 如图,在平面直角坐标系中, 轴,垂足为 ,将 绕点 逆时针旋转到 的位置,使点 的对应点 落在直线 上,再将 绕点 逆时针旋转到 的位置,使点 的对应点 也落在直线 上,以此进行下去……若点 的坐标为 ,则点 的纵坐标为.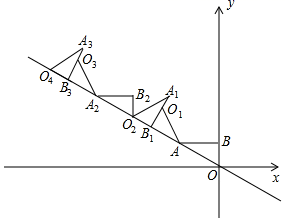
三、解答题
-
19.
如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(−2,−2),B(−4,−1),C(−4,−4).
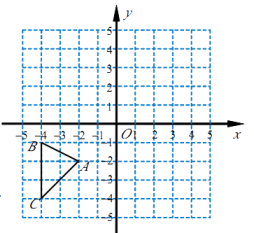 (1)、作出 ABC关于原点O成中心对称的 A1B1C1.(2)、作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.20. 如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ =0,点C的坐标为(0,3)。
(1)、作出 ABC关于原点O成中心对称的 A1B1C1.(2)、作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.20. 如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+ =0,点C的坐标为(0,3)。 (1)、求a,b的值及S三角形ABC;(2)、若点M在x轴上,且S三角形ACM= S三角形ABC , 试求点M的坐标。21. 如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 和 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由.
(1)、求a,b的值及S三角形ABC;(2)、若点M在x轴上,且S三角形ACM= S三角形ABC , 试求点M的坐标。21. 如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 和 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由. 22. 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
22. 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).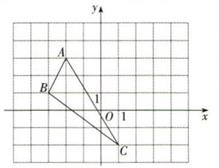 (1)、直接写出点A、B、C关于y轴对称的点A'、B'、C'的坐标;(2)、在x轴上求作一点P,使PA+PB最短(保留痕迹).23. 如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).
(1)、直接写出点A、B、C关于y轴对称的点A'、B'、C'的坐标;(2)、在x轴上求作一点P,使PA+PB最短(保留痕迹).23. 如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).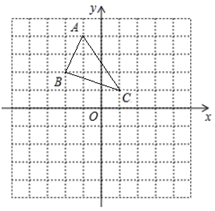 (1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.24. 如图所示是某学校周边环境示意图.对于学校来说:
(1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.24. 如图所示是某学校周边环境示意图.对于学校来说: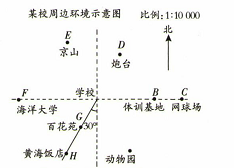 (1)、学校正东有哪些设施?要明确这些设施相对于学校的位置还需要什么?(2)、离学校最近的设施是什么?方向是什么?这一方向上还有什么其他设施?(3)、要确定动物园相对于学校的位置,需要哪几个数据?25. 如图,在平面直角坐标系 中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
(1)、学校正东有哪些设施?要明确这些设施相对于学校的位置还需要什么?(2)、离学校最近的设施是什么?方向是什么?这一方向上还有什么其他设施?(3)、要确定动物园相对于学校的位置,需要哪几个数据?25. 如图,在平面直角坐标系 中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动). (1)、点B的坐标为;(2)、当点P移动4s时,求出点P的坐标;(3)、在移动过程中,当点P到 轴的距离为5个单位长度时,求点P移动的时间t .
(1)、点B的坐标为;(2)、当点P移动4s时,求出点P的坐标;(3)、在移动过程中,当点P到 轴的距离为5个单位长度时,求点P移动的时间t .