初中数学华师大版七年级上学期第3章整式的加减单元测试

试卷更新日期：2021-10-06 类型：单元试卷

进入出卷网下载

一、单选题

1. 某种商品m千克的售价为n元，那么这种商品8千克的售价为（）

A、 $\frac{8 n}{m}$ （元） B、 $\frac{n}{8 m}$ （元） C、 $\frac{8 m}{n}$ （元） D、 $\frac{m}{8 n}$ （元）

查看试题解析
2. 若a+b＝﹣1，则（a+b）²的值是（　　）

A、﹣1 B、﹣2 C、2 D、1

查看试题解析
3. 若 $\frac{1}{2}$ a^3xb^y与﹣a^2yb^x⁺¹是同类项，则x ， y的值为（）

A、 ${\begin{matrix} x = - 2 \\ y = 3 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ C、 ${\begin{matrix} x = - 2 \\ y = - 3 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

查看试题解析
4. 已知a+b=4，则代数式 $1 + \frac{a}{2} + \frac{b}{2}$ 的值为（）

A、3 B、1 C、0 D、-1

查看试题解析
5. 如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），输出的结果为（）

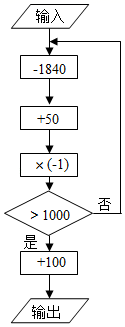A、1840 B、1921 C、1949 D、2021

查看试题解析
6. 一质点 $P$ 从距原点8个单位的 $M$ 点处向原点方向跳动.第一次跳动到 $O M$ 的中点 $M_{1}$ 处，第二次从 $M_{1}$ 跳到 $O M_{1}$ 的中点 $M_{2}$ 处，第三次从点 $M_{2}$ 跳到 $O M_{2}$ 的中点 $M_{3}$ 处，如此不断跳动下去，则第2021次跳动后，该质点到原点 $O$ 的距离为（）

A、 $2^{- 2018}$ B、 $2^{- 2019}$ C、 $2^{- 2020}$ D、 $2^{- 2021}$

查看试题解析
7. 如 $M = {1 ， 2 ， x}$ ，我们叫集合 $M$ ，其中1，2， $x$ 叫做集合 $M$ 的元素.集合中的元素具有确定性（如 $x$ 必然存在），互异性（如 $x \neq 1$ ， $x \neq 2$ ），无序性（即改变元素的顺序，集合不变）.若集合 $N = {x ， 1 ， 2}$ ，我们说 $M = N$ .已知集合 $A = {1 ， 0 ， a}$ ，集合 $B = {\frac{1}{a} ， | a | ， \frac{b}{a}}$ ，若 $A = B$ ，则 $b - a$ 的值是（）

A、－1 B、0 C、1 D、2

查看试题解析

8. 我们根据指数运算，得出了一种新的运算，如表所示是两种运算对应关系的一组实例：

指数运算	2¹=2	2²=4	2³=8	……	3¹=3	3²=9	3³=27	……
新运算	log₂2= 1	log₂4= 2	log₂8= 3	……	log₃3= 1	log₃9= 2	log₃27= 3	……

根据上表规律，某同学写出了三个式子：①log₂16= 4，②log₅ 25=5，③log₂ $\frac{1}{2}$ =-1．其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

9. 观察下列等式：
①3²﹣1²＝2×4

②5²﹣3²＝2×8

③7²﹣5²＝2×12……

那么第n（n为正整数）个等式为（）

A、n²﹣（n﹣2）²＝2×（2n﹣2） B、（n＋1）²﹣（n﹣1）²＝2×2n C、（2n）²﹣（2n﹣2）²＝2×（4n﹣2） D、（2n＋1）²﹣（2n﹣1）²＝2×4n

查看试题解析

二、填空题

10. 计算 $5 x - 3 x + 4 x$ 的结果等于．

查看试题解析
11. 已知x+2y=2，则1－2x－4y的值等于.

查看试题解析
12. 对于任意实数a，b，定义关于“⊗”的一种运算如下：a⊗b＝2a﹣b.例如3⊗4＝2×3﹣4＝2.若x⊗y＝2，且y⊗x＝4，则x+y的值为.

查看试题解析
13. 在平面直角坐标系中，点P(x，y)经过某种变换后得到点P'(-y+1，x+2)，我们把点P'(-y+1，x+2)叫做点P(x，y)的终结点已知点P₁的终结点为P₂ ，点P₂的终结点为P₃ ，点P₃的终结点为P₄ ，这样依次得到P₁、P₂、P₃、P₄、……、P_n ，若点P₁的坐标为(2，0) ，则点P₂₀₂₁的坐标为

查看试题解析
14. 如图

（问题提出）：将一个边长为 $n$ （ $n$ ≥2）的正方形的四条边 $n$ 等分，连接各边对应的等分点，则该正方形被剖分的网格中的长方形的个数（此处长方形包括正方形）和正方形个数分别是多少？

（问题探究）：要研究上面的问题，我们不妨先从特例入手，进而找到一般规律．

探究一：将一个边长为2的正方形的四条边分别 2 等分，连接各边对应的等分点，则该正方形被剖分的网格中的长方形的个数（此处长方形包括正方形）和正方形个数分别是多少？

如图1，从上往下，共有2行，我们先研究长方形（此处长方形包括正方形）的个数：

①第一行有宽边长为1，底长为1～2的长方形，共有2+1=3个；

②第二行有宽边长为1，底长为1～2的长方形，共有2+1=3个；

为了便于归纳分析，我们把长方形下面的底在第二行的所有长方形均算作第二行的长方形，以下各行类同第二行．因此底第二行还包括宽边长为2，底长为1～2 的长方形，共有2+1=3个．

即：第二行长方形共有 2×3个．

所以如图1，长方形共有 2×3+3=9=（2+1）²

我们再研究正方形的个数：

分析：边长为1的正方形共有2²个，边长为2的正方形共有1²个，

所以：如图 1，正方形共有2² + 1² = 5 = $\frac{1}{6}$ ×2×3×5 个．

探究二：将一个边长为3的正方形的四条边分别3等分，连接各边对应的等分点，则该正方形被剖分的网格中的长方（此处长方形包括正方形）的个数和正方形个数分别是多少？

如图2，从上往下，共有3行，我们先研究长方形的个数：

①第一行有宽长为1底长为1～3 的长方形，共有3+2+1=6个；

②第二行有宽边长为1，底长为 1～3的长方形，共有3+2+1=6个；

底在第二行还包括宽边长为2，底长为1～3 的长方形，共有3+2+1=6个．

即：第二行长方形共有2×6个．

③第三行有宽边长为1，底长为1～3 的长方形，共有3+2+1=6个；

底在第三行还包括宽边长为 2，底长为 1～3 的长方形，共有 3+2+1=6个．

底在第三行还包括宽边长为 3，底长为 1～3 的长方形，共有 3+2+1=6个．

即：第三行长方形共有 3×6个．

所以如图 2，长方形共有 3×6+2×6+6=（3+2+1）×6=（3+2+1）² ．

我们再研究正方形的个数：分析：边长为1的正方形共有 3²个，边长为 2 的正方形共有 2²个，边长为 3 的正方形共有 1²个．

所以：如图2，正方形共有 3² + 2² + 1² =14 = $\frac{1}{6}$ ×3×4×7 个．

探究三：将一个边长为 5 的正方形的四条边分别 5 等分，连接各边对应的等分点，则该正方形被剖分的网格中的长方形（此处长方形包括正方形）的个数和正方形个数分别是多少？

(1)、如图 3，从上往下，共有 5 行，我们先研究长方形的个数：
①第一行有宽边长为 1，底长为 1～5 的长方形，共有 5+4+3+2+1=15个；

②第二行有宽边长为 1，底长为 1～5 的长方形，共有 5+4+3+2+1=15个；底在第二行还包括宽边长为 2，底长为 1～5 的长方形，共有 5+4+3+2+1=15个．即：第二行长方形共有2×15个．

③模仿上面的探究，第三行长方形总共有 3×15 个．

④按照上边的规律，第四行长方形总共有个．

⑤按照上边的规律，第五行长方形总共有个．

所以，如图 3，长方形总共有个．

我们再研究正方形的个数：

分析：边长为 1 的正方形共有 5²个，边长为 2 的正方形共有 4²个，边长为 3 的正方形共有 3²个，边长为 4 的正方形共有 2²个，边长为 5 的正方形共有1²个．

所以：如图 3，正方形共有5 ²+ 4² + 3² + 2²+ 1² = $\frac{1}{6}$ ×个．（仿照前面的探究，写成三个整数相乘的形式）

(2)、（问题解决）将一个边长为 $n$ （ $n$ ≥2）的正方形的四条边 $n$ 等分，连接各边对应的等分点，根据上边的规律，得出该正方形被剖分的网格中的长方形（此处矩形包括正方形）的个数是和正方形个数分别是 $\frac{1}{6}$ × ．（用含 $n$ 的代数式表示）
（问题应用）将一个边长为 $n$ （ $n$ ≥2）的正方形的四条边 12 等分，连接各边对应的等分点，若得出该正方形被剖分的网格中的长方形的（此处长方形包括正方形）个数

是个，正方形个数是个．

查看试题解析

三、解答题

15. 用※定义一种新运算：对于任意实数m和n，规定m※n=mn-2m，
如：3※4=3×4-2×3

若(3-π)※x≥0，求x的取值范围

查看试题解析
16. 观察下列等式：9﹣1＝2×4，16﹣4＝3×4，25﹣9＝4×4，36﹣16＝5×4，…，这些等式反映自然数间的某种规律，设n表示自然数，请猜想出这个规律，用含n的等式表示出来，并加以证明．

查看试题解析

四、综合题

17. 观察下列各式的规律：
① $1 \times 4 - 2^{2} = 0$ ；② $2 \times 5 - 3^{2} = 1$ ；③ $3 \times 6 - 4^{2} = 2$ ；…

根据上述式子的规律，解答下列问题：

(1)、第④个等式为.

(2)、写出第n个等式，并验证其正确性.

查看试题解析
18. 一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果x=y，那么称这个四位数为“和平数”.例如：1423，x=1+4，y=2+3，因为x=y，所以1423是“和平数”.

(1)、请判断：2561(填“是”或“不是”)“和平数”

(2)、直接写出：最小的“和平数”是，最大的“和平数”是

(3)、如果一个“和平数”的个位上的数字是千位上的数字的两倍，且百位上的数字与十位上的数字之和是14的倍数，求满足条件的所有“和平数”.

查看试题解析