初中数学华师大版七年级上学期第3章3.4整式的加减同步练习

试卷更新日期：2021-10-06 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各式中，与 $2 a^{2} b$ 为同类项的是（）

A、 $- 2 a^{2} b$ B、 $- 2 a b$ C、 $2 a b^{2}$ D、 $2 a^{2}$

查看试题解析
2. $- 2 (1 - x) =$ （）

A、 $- 2 + 2 x$ B、 $- 2 - 2 x$ C、 $- 2 + x$ D、 $- 2 - x$

查看试题解析
3. 若x^a^﹣¹y^2b与﹣2x²^﹣^by²是同类项，则a、b的值分别是（　　）

A、a＝2，b＝﹣1 B、a＝﹣2，b＝﹣1 C、a＝2，b＝1 D、a＝﹣2，b＝1

查看试题解析
4. 已知 $2 x^{6} y^{2}$ 和 $- \frac{1}{3} x^{3 m} y^{n}$ 是同类项，则 $9 m^{2} - 5 m n - 17$ 的值是（）

A、-1 B、-2 C、-3 D、-4

查看试题解析
5. 如图是一个由 5 张纸片拼成一个大长方形，相邻纸片之间互不重叠也无缝隙，其中两张大正方形纸片大小一样，面积记为S₁ ，另外两张长方形纸片大小一样，面积记为S₂ ，中间一张小正方形纸片的面积记为S₃ ，则这个大长方形的面积一定可以表示为（）

A、 $3 S_{1} + S_{2}$ B、 $S_{1} + 4 S_{2}$ C、 $4 S_{1}$ D、 $4 S_{2}$

查看试题解析
6. 已知 $- 2 x^{m - 1} y^{3}$ 与 $x^{n} y^{m + n}$ 是同类项，那么 ${(n - m)}^{2021}$ 的值是（）

A、1 B、-1 C、 $2^{2021}$ D、0

查看试题解析
7. 如图，两个长方形的面积分别为20，6，两阴影部分的面积分别为a ， b ，且 $a > b$ ，则 $(a - b)$ 等于（）

A、6 B、7 C、14 D、16

查看试题解析
8. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，且 $| c | > | a | > | b |$ ，则 $| a + b | - 2 | c - b | + | a + c | =$ （）．

A、 $c - b$ B、0 C、 $3 b - 3 c$ D、 $2 a + 3 b - c$

查看试题解析
9. 在矩形ABCD内，将两张边长分别为a和b(a>b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为l，若要知道l的值，只要测量图中哪条线段的长（）

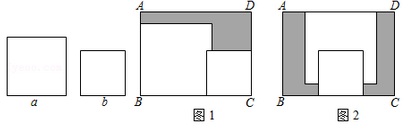A、a B、b C、AD D、AB

查看试题解析

二、填空题

10. 计算 $2 a^{2} + 3 a^{2} - a^{2}$ 的结果等于．

查看试题解析
11. 如果单项式 $3 a^{2 x} b^{y}$ 与单项式 $- 2 a^{y} b^{x + 2}$ 是同类项，则 $y^{x}$ 的值为.

查看试题解析
12. 添括号：3（a-b）²-a+b=3（a-b）²-（）

查看试题解析
13. 如果单项式 $2 x^{m - 1} y^{2}$ 与 $- 3 x^{2} y^{n + 1}$ 是同类项，那么 $m + n =$ ．

查看试题解析
14. 将7张相同的小长方形纸片（如图1所示）按图2所求的方式不重叠的放在长方形 $A B C D$ 内，未被覆盖的部分恰好被分割为两个长方形，面积分别为 $S_{1} ， S_{2}$ ，已知小长方形纸片的长为 $a$ ，宽为 $b$ ，且 $a > b$ ．若 $A B$ 长度不变， $A D$ 变长，将这7张小长方形纸片还按照同样的方式放在新的长方形 $A B C D$ 内，而 $S_{1} - S_{2}$ 的值总保持不变，则 $a ， b$ 满足的关系是．

查看试题解析

三、综合题

15. 若一个各位数字均不为零的四位自然数 $A$ 满足千位数字与十位数字相等，百位数字与个位数字相等（且千位数字与百位数字不等），我们称这样的数 $A$ 叫“前进数”；当我们把“前进数” $A$ 千位、百位上的数字交换，十位与个位上的数字交换得到另外一个数 $A^{'}$ .

(1)、6556（填“是”或“否”）为“前进数”；最小的“前进数”为.

(2)、求证：任意的“前进数” $A$ 与 $A^{'}$ 的和都可以被11整除；

(3)、规定：前进数 $A$ 满足 $f (A) = \frac{(A + A^{'})}{101}$ ，若 $f (A)$ 能被13整除，且千位数字小于百位数字，求出所有满足条件的“前进数”.

查看试题解析
16. 有甲、乙两个长方形纸片，边长如图所示（m＞0），面积分别为S_甲和S_乙．

(1)、①计算：S_甲＝， S_乙＝；
②用“＜”，“＝”或“＞”填空：S_甲 S_乙．

(2)、若一个正方形纸片的周长与乙长方形的周长相等，面积为S_正．
①该正方形的边长是 ▲ （用含m的代数式表示）；

②小方同学发现：S_正与S_乙的差与m无关．请判断小方的发现是否正确，并通过计算说明你的理由．

查看试题解析