北师版数学八年级上册第一次月考A卷（第一二章综合）

试卷更新日期：2021-10-05 类型：月考试卷

进入出卷网下载

一、单选题

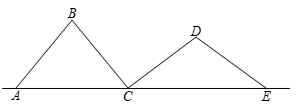
1. 下列各数中，为无理数的是（）

A、 $π$ B、 $\frac{22}{7}$ C、0 D、-2

查看试题解析
2. 16的平方根是（）

A、 ±4 B、4 C、±8 D、8

查看试题解析
3. 如图， $A B$ 、 $B C$ 、 $C D$ 、 $D E$ 是四根长度均为5cm的火柴棒，点A、C、E共线.若 $A C = 6 cm$ ， $C D ⊥ B C$ ，则线段 $C E$ 的长度为（）

A、6 cm B、7 cm C、 $6 \sqrt{2} cm$ D、8cm

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = 3$ B、 $4 \sqrt{5} - \sqrt{5} = 4$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{32} \div \sqrt{8} = 4$

查看试题解析
5. 我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭（jiǎ）生其中，出水一尺，引葭赴岸，适与岸齐.间水深几何.”（丈、尺是长度单位，1丈 $= 10$ 尺，）其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺.如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度是多少？则水深为（）

A、10尺 B、11尺 C、12尺 D、13尺

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 ${(- 2)}^{0} = 1$ C、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ D、 $\sqrt[3]{9} = 3$

查看试题解析
7. 如图，点 $A$ ， $B$ 都在格点上，若 $B C= \frac{2 \sqrt{13}}{3}$ ，则 $A C$ 的长为（）

A、 $\sqrt{13}$ B、 $\frac{4 \sqrt{13}}{3}$ C、 $2 \sqrt{13}$ D、 $3 \sqrt{13}$

查看试题解析
8. 计算 $\sqrt{12} - \sqrt{12} \times \sqrt{\frac{1}{4}}$ 的结果是（）

A、0 B、 $\sqrt{3}$ C、 $3 \sqrt{3}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图，在矩形ABCD中，AB＝5，AD＝3，点E为BC上一点，把△CDE沿DE翻折，点C 恰好落在AB边上的F处，则CE的长是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析
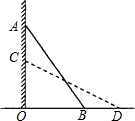
10. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A、1，4，5 B、2，3，5 C、3，4，5 D、2，2，4

查看试题解析
11. 已知 $43^{2} = 1849 ， 44^{2} = 1936 ， 45^{2} = 2025 ， 46^{2} = 2116$ ．若 $n$ 为整数且 $n < \sqrt{2021} < n + 1$ ，则 $n$ 的值为（）

A、43 B、44 C、45 D、46

查看试题解析
12. 《九章算术》是古代东方数学代表作，书中记载：今有开门去阃(读 $k u n$ ，门槛的意思)一尺，不合二寸，问门广几何？题目大意是：如图1、2(图2为图1的平面示意图)，推开双门，双门间隙 $C D$ 的距离为 $2$ 寸，点 $C$ 和点 $D$ 距离门槛 $A B$ 都为 $1$ 尺( $1$ 尺 $= 10$ 寸)，则 $A B$ 的长是（）

A、 $50.5$ 寸 B、 $52$ 寸 C、 $101$ 寸 D、 $104$ 寸

查看试题解析

二、填空题

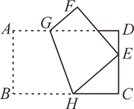
13. 若二次根式 $\sqrt{2 x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是.

查看试题解析
14. 如图，折叠矩形纸片ABCD ，使点B的对应点E落在CD边上，GH为折痕，已知 $A B = 6$ ， $B C = 10$ ．当折痕GH最长时，线段BH的长为．

查看试题解析
15. 一个正数a的两个平方根是 $2 b - 1$ 和 $b + 4$ ，则 $a + b$ 的立方根为．

查看试题解析
16. 《九章算术》是我国古代数学名著，书中有下列问题：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广各几何？”其意思为：今有一门，高比宽多6尺8寸，门对角线距离恰好为1丈.问门高、宽各是多少？（1丈＝10尺，1尺＝10寸）如图，设门高 $A B$ 为 $x$ 尺，根据题意，可列方程为.

查看试题解析
17. 2021年5月7日，《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家，他是第一个将圆周率 $π$ 精确到小数点后第七位的人，他给出 $π$ 的两个分数形式： $\frac{22}{7}$ （约率）和 $\frac{355}{113}$ （密率）.同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数 $x$ 的不足近似值和过剩近似值分别为 $\frac{b}{a}$ 和 $\frac{d}{c}$ （即有 $\frac{b}{a} < x < \frac{d}{c}$ ，其中 $a$ ， $b$ ， $c$ ， $d$ 为正整数），则 $\frac{b + d}{a + c}$ 是 $x$ 的更为精确的近似值.例如：已知 $\frac{157}{50} < π < \frac{22}{7}$ ，则利用一次“调日法”后可得到 $π$ 的一个更为精确的近似分数为： $\frac{157 + 22}{50 + 7} = \frac{179}{57}$ ；由于 $\frac{179}{57} \approx 3.1404 < π$ ，再由 $\frac{179}{57} < π < \frac{22}{7}$ ，可以再次使用“调日法”得到 $π$ 的更为精确的近似分数……现已知 $\frac{7}{5} < \sqrt{2} < \frac{3}{2}$ ，则使用两次“调日法”可得到 $\sqrt{2}$ 的近似分数为.

查看试题解析
18. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 $A B C D$ ，对角线 $A C 、 B D$ 交于点O．若 $A D = 2 ， B C = 4$ ，则 $A B^{2} + C D^{2} =$ ．

查看试题解析

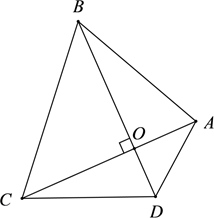
三、解答题

19. 计算： $(2 \sqrt{6} + \sqrt{\frac{2}{3}}) \times \sqrt{3} - \sqrt{32}$ .

查看试题解析
20. 计算．

(1)、 $(\sqrt{48} - 3 \sqrt{6}) \div \sqrt{3} + \sqrt{18}$ ；

(2)、 $4 \sqrt{\frac{1}{2}} - \sqrt{8} + \sqrt{27} \times \sqrt{\frac{1}{3}} - {(\sqrt{3})}^{0}$ ；

(3)、 ${(\sqrt{3} - \sqrt{5})}^{2} - {(\sqrt{3} + \sqrt{5})}^{2}$ ．

查看试题解析
21. 已知 $1 + 3 a$ 的平方根是 $\pm 7$ ， $2 a - b - 5$ 的立方根是-3， $c$ 是 $\sqrt{123}$ 的整数部分，求 $a + b + c$ 的平方根．

查看试题解析
22. 阅读理解：
∵ $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即2< $\sqrt{5}$ <3，∴1< $\sqrt{5}$ -1<2，

∴ $\sqrt{5}$ -1的整数部分为1，

∴ $\sqrt{5}$ -1的小数部分为 $\sqrt{5}$ -2

解决问题：

已知a是 $\sqrt{17}$ -3的整数部分，b是 $\sqrt{17}$ -3的小数部分，求(-a)³+(b+4)²的平方根

查看试题解析
23. 如图，将矩形ABCD沿对角线BD所在直线折叠，点C落在同一平面内，落点记为F，BF与AD交于点E，若AB＝4，BC＝8，求BE的长．

查看试题解析
24. 如图，一架梯子 $A B$ 斜靠在一竖直的墙 $O A$ 上，这时 $A O = 2.5 m$ ， $∠ O A B = 30 °$ ．梯子顶端 $A$ 沿墙下滑至点 $C$ ，使 $∠ O C D = 60 °$ ，同时，梯子底端 $B$ 也外移至点 $D$ ．求 $B D$ 的长度．（结果保留根号）

查看试题解析
25. 已知 $2 a - 1$ 的算术平方根是 $3$ ， $3 a + b - 1$ 的平方根是 $\pm 4$ ， $c$ 是 $\sqrt{13}$ 的整数部分，求 $a + 2 b - c^{2}$ 的平方根

查看试题解析