湘教版数学九年级上册同步训练《5.2 统计的简单应用》
试卷更新日期:2021-10-03 类型:同步测试
一、单选题
-
1. 如图是某天参观温州数学名人馆的学生人数统计图.若大学生有60人,则初中生有( )
某天参观温州数学名人馆的学生人数统计图
 A、45人 B、75人 C、120人 D、300人2. 在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).
A、45人 B、75人 C、120人 D、300人2. 在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).类型
健康
亚健康
不健康
数据(人)
32
7
1
A、32 B、7 C、 D、3. 如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,每周课外阅读时间不少于6小时的人数是( ) A、6人 B、8人 C、14人 D、36人4. 某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),数据分成6组: , , , , ,如图是根据数据绘制的统计图.下列说法正确的是( )
A、6人 B、8人 C、14人 D、36人4. 某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),数据分成6组: , , , , ,如图是根据数据绘制的统计图.下列说法正确的是( )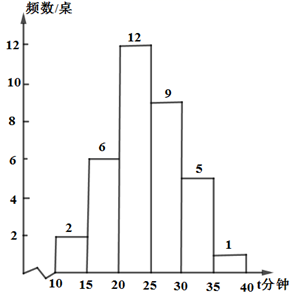 A、此时段有1桌顾客等位时间是40分钟 B、此时段平均等位时间小于20分钟 C、此时段等位时间的中位数可能是27 D、此时段有6桌顾客可享受优惠5. 某射击运动员在训练中射击了10次,成绩如图所示:
A、此时段有1桌顾客等位时间是40分钟 B、此时段平均等位时间小于20分钟 C、此时段等位时间的中位数可能是27 D、此时段有6桌顾客可享受优惠5. 某射击运动员在训练中射击了10次,成绩如图所示: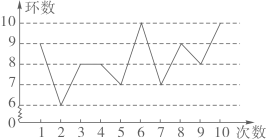
下列结论错误的是( )
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是1.26. 为了解某校学生每周课外阅读时间的情况,随机抽取该校a名学生进行调查,获得的数据整理后绘制成统计表如下:每周课外阅读时间x(小时)
0≤x<2
2≤x<4
4≤x<6
6≤x<8
x≥8
合计
频数
8
17
b
15
a
频率
0.08
0.17
c
0.15
1
表中4≤x<6组的频数b满足25≤b≤35.下面有四个推断:
①表中a的值为100;②表中c的值可以为0.31;③这a名学生每周课外阅读时间的中位数一定不在6~8之间;④这a名学生每周课外阅读时间的平均数不会超过6.
所有合理推断的序号是( )
A、①② B、③④ C、①②③ D、②③④7. 某校九年级学生中考体育选考项目组合情况的统计图如图所示,若九年级学生共有400人,则选择跳远、游泳、篮球项目组合的有( ) A、60人 B、80人 C、120人 D、140人8. 某校学生会主席竞选中,参与投票的学生必须从进入决赛的四名选手中选1名,且只能选1名进行投票,根据投票结果,绘制了如下两幅不完整的统计图,则选手B的得票数为( )
A、60人 B、80人 C、120人 D、140人8. 某校学生会主席竞选中,参与投票的学生必须从进入决赛的四名选手中选1名,且只能选1名进行投票,根据投票结果,绘制了如下两幅不完整的统计图,则选手B的得票数为( )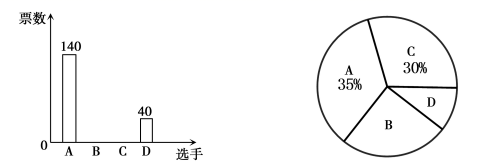 A、80 B、90 C、100 D、4009. 据统计,我市今年十一月份日平均气温的分布情况如下表:
A、80 B、90 C、100 D、4009. 据统计,我市今年十一月份日平均气温的分布情况如下表:平均气温(℃)
13
14
15
16
17
天数
3
7
3
9
8
其中频数最高的气温(℃)是( )
A、17 B、16 C、15 D、1410. 某校测量了初三 班学生的身高(精确到 ),按 为一段进行分组,得到如下频数分布直方图,则下列说法正确的是( )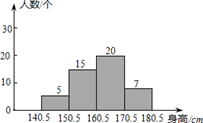 A、该班人数最多的身高段的学生数为
A、该班人数最多的身高段的学生数为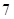 人
B、该班身高低于
人
B、该班身高低于 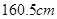 的学生数为
的学生数为 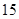 人
C、该班身高最高段的学生数为
人
C、该班身高最高段的学生数为 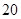 人
D、该班身高最高段的学生数为
人
D、该班身高最高段的学生数为 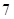 人
人
二、填空题
-
11. 2021年春季各校采取年段错峰用餐,某校为了了解学生在校午餐所需时间,抽取20名学生在校用餐时间,并绘制成频数分布直方图(如图),根据图象信息,预估该校学生平均用餐时间是分钟.
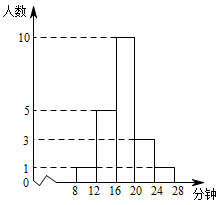 12. 某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有人.
12. 某城市抽查一些家庭每月水电费的开支(单位:元),得到如图所示的频数直方图(每一组包括前一个边界值,不包括后一个边界值),则抽查到的家庭每月开支在225元及以上的有人. 13. 某班甲、乙、丙三名同学20天的体温数据记录如下表:
13. 某班甲、乙、丙三名同学20天的体温数据记录如下表:甲的体温
乙的体温
丙的体温
温度(℃)
36.1
36.4
36.5
36.8
温度(℃)
36.1
36.4
36.5
36.8
温度(℃)
36.1
36.4
36.5
36.8
频数
5
5
5
5
频数
6
4
4
6
频数
4
6
6
4
则在这20天中,甲、乙、丙三名同学的体温情况最稳定的是 .
14. 某班同学进行数学测试,将所得成绩(整数)进行整理后分成五组,并绘制成如图的频数分布直方图,则这次成绩的中位数落在这一分数段内(填具体分数). 15. 某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
15. 某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
根据以上统计图提供的信息,则D等级这一组人数较多的班是
16. 今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查,图1和图2是收集数据后绘制的两幅不完整统计图.根据图中提供的信息,那么本次调查的对象中选择公交前往的人数是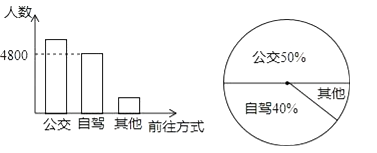
三、解答题
-
17. 某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分):整理、分析过程如下,请补充完整.
 (1)、按如下分数段整理、描述这两组数据:
(1)、按如下分数段整理、描述这两组数据:成绩x
学生
70≤x≤74
75≤x≤79
80≤x≤84
85≤x≤89
90≤x≤94
95≤x≤100
甲
乙
1
1
4
2
1
1
(2)、两组数据的极差、平均数、中位数、众数、方差如下表所示:学生
极差
平均数
中位数
众数
方差
甲
83.7
86
13.21
乙
24
83.7
82
46.21
(3)、若从甲、乙两人中选择一人参加知识竞赛,你会选谁(填“甲”或“乙),理由是什么.18. “读书,点亮未来”,广泛的课外阅读是同学们搜集和汲取知识的一条重要途径.学校图书馆计划购进一批学生喜欢的图书,为了了解学生们对“A文史类、B科普类、C生活类、D其它”的喜欢程度,随机抽取了部分学生进行问卷调查(每个学生只选其中一类),将所得数据进行分类统计绘制了如下不完整的统计图表,请根据图中的信息,解答下列问题:统计表:
频数
频率
A历史类
50
m
B科普类
90
0.45
C生活类
n
0.20
D其它
20
0.10
合计
 (1)、本次调查的学生共人;(2)、 , ;(3)、补全条形统计图.19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:
(1)、本次调查的学生共人;(2)、 , ;(3)、补全条形统计图.19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:甲厂:76,74,74,76,73,76,76,77,78,74,76,70,76,76,73,70,77,79,78,71;
甲厂鸡腿质量频数统计表
质量 ( )
频数
频率
2
0.1
3
0.15
10
5
0.25
合计
20
1
乙厂:75,76,77,77,78,77,76,71,74,75,79,71,72,74,73,74,70,79,75,77;
乙厂鸡腿质量频数分布直方图

分析上述数据,得到下表:
统计量
厂家
平均数
中位数
众数
方差
甲厂
75
76
6.3
乙厂
75
75
77
6.6
请你根据图表中的信息完成下列问题:
(1)、 , ;(2)、补全频数分布直方图;(3)、如果只考虑出口鸡腿规格,请结合表中的某个统计量,为外贸公司选购鸡腿提供参考建议;(4)、某外贸公司从甲厂采购了20000只鸡腿,并将质量(单位: )在 的鸡腿加工成优等品,请估计可以加工成优等品的鸡腿有多少只?20. 截止到2020年11月,我国贫困县“摘帽”计划已经全部完成,脱贫攻坚取得了全面胜利!为了打赢“脱贫攻坚”战役,国家设立了“中央财政脱贫专项资金”以保证对名省贫困地区的持续投入,小凯同学通过登录国家乡村振兴局网站,查询到了2020年中央财政脱贫专项资金对我国28个省、直辖市、自治区的分配额度(亿元),并对数据进行整理、描述和分析.下面是小凯给出的部分信息.a.反映2020年中央财政脱贫专项资金分配额度的频数分布直方图如下(数据分成8组: , , , , , , , )
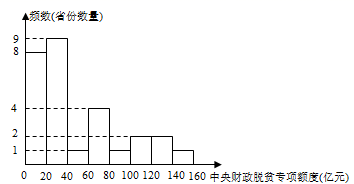
b.2020年中央财政脱贫专项资金在 这一组分配的额度是(亿元):
25;28;28;30;37;37;38;39;39
(1)、2020年中央财政脱贫专项资金对各省、直辖市、自治区分配额度的中位数为(亿元);(2)、2020年中央财政脱贫专项资金对某省的分配额度为95亿元,该额度在28个省、直辖市、自治区中由高到低排第名;(3)、小凯在收集数据时得到了2016-2020年中央财政脱贫专项资金对自治区A和自治区B的分配额度变化图: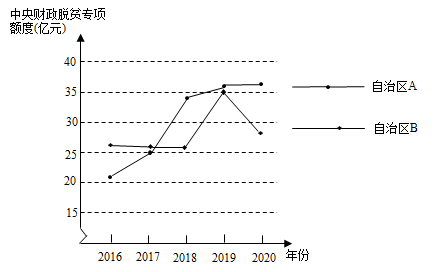
①比较2016年-2020年中央财政脱贫专项资金对自治区A,B的分配额度,方差 ▲ _ (填写“>”或者“<”);
②请结合统计数据,针对中央财政脱贫专项资金对自治区A,B脱贫攻坚工作的支持情况,说一说你的看法.
21. 某校为了了解八年级学生线上课堂发言情况,将随机抽取的该年级部分学生某一天在线上课堂上发言次数统计如下表,并绘制了如图所示的两幅不完整的统计图.请给合图中相关数据回答下列问题:组别
发言次数
A
B
C
D
E

 (1)、此次调查的样本容量为 , , ;(2)、请补全直方图;(3)、在扇形统计图中, 组所对应的圆心角的度数为°, 组所占的百分比为%;(4)、该年级共有学生1500人,估计全年级这天发言次数不少于6次的有人.22. 垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用.为了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃圾分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(1)、此次调查的样本容量为 , , ;(2)、请补全直方图;(3)、在扇形统计图中, 组所对应的圆心角的度数为°, 组所占的百分比为%;(4)、该年级共有学生1500人,估计全年级这天发言次数不少于6次的有人.22. 垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用.为了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃圾分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80.
乙班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83.
(1)、(整理数据)按如下分数段整理、描述这两组样本数据组别
65.5~70.5
70.5~75.5
75.5~80.5
80.5~85.5
85.5~90.5
90.5~95.5
甲
2
2
4
5
1
1
乙
1
1
a
b
2
0
在表中,a= , b= .
(2)、补全甲班15名学生测试成绩的频数分布直方图.
(分析数据)
班级
平均数
众数
中位数
方差
甲
80
x
80
47.6
乙
80
80
y
26.2
(3)、两组样本数据的平均数、众数、中位数、方差如表所示:在表中:x= , y= .(4)、若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃圾分类及投放相关知识合格的学生有人.(5)、你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.