湘教版数学九年级上册同步训练《5.1 总体平均数与方差的估计》
试卷更新日期：2021-10-03 类型：同步测试
一、单选题
-
1. 下列说法正确的是（ ）A、了解市民知晓“礼让行人”交通新规的情况，适合全面调查 B、一组数据5，5，3，4，1的中位数是3 C、甲、乙两人9次跳高成绩的方差分别为 甲2 ， 乙2 ，说明乙的成绩比甲稳定 D、“经过有交通信号灯的路口，遇到红灯”是随机事件2. 一组数据8，7，8，6，4，9的中位数和平均数分别是（ ）A、7和8 B、7.5和7 C、7和7 D、7和7.53. 某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表：
项目
作品
甲
乙
丙
丁
创新性
90
95
90
90
实用性
90
90
95
85
如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（ ）
A、甲 B、乙 C、丙 D、丁4. 为增强学生的环保意识，共建绿色文明校园.某学校组织“废纸宝宝旅行记”活动.经统计，七年级5个班级一周回收废纸情况如下表；班级
一班
二班
三班
四班
五班
废纸重量（ ）
4.5
4.4
5.1
3.3
5.7
则每个班级回收废纸的平均重量为（ ）
A、 B、 C、 D、5. 下列说法正确的是（ ）A、“打开电视机，正在播放《新闻联播》”是必然事件 B、“明天下雨概率为0.5”，是指明天有一半的时间可能下雨 C、一组数据“6，6，7，7，8”的中位数是7，众数也是7 D、甲､乙两人在相同的条件下各射击10次，他们成绩的平均数相同.方差分别是 ， ，则甲的成绩更稳定6. 某校九年级进行了3次数学模拟考试，甲、乙、丙三名同学的平均分为及方差 如右表所示，那么这三名同学数学成绩最稳定的是（ ）甲
乙
丙
91
91
91
6
24
54
A、甲 B、乙 C、丙 D、无法确定7. 对于一组数据1，1，3，1，4，下列结论不正确的是（ ）A、平均数是2 B、众数是1 C、中位数是3 D、方差是1.68. 一组数据4，6，x，7，10的众数是7，则这组数据的平均数是（ ）A、5 B、6.4 C、6.8 D、79. 一组数据：1，2，2，3，若添加一个数据3，则不发生变化的统计量是（ ）A、平均数 B、中位数 C、众数 D、方差10. 小亮要计算一组数据80，82，74，86，79的方差 ，在计算平均数的过程中，将这组数据中的每一个数都减去80，得到一组新数据0，2，-6，6，-1，记这组新数据的方差为 ，则 与 的大小关系为（ ）A、 B、 C、 D、无法确定二、填空题
-
11. 中药是以我国传统医药理论为指导，经过采集、炮制、制剂而得到的药物.在一个时间段，某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如下表：
中药
黄芪
焦山楂
当归
销售单价（单位：元/千克）
80
60
90
销售额（单位：元）
120
120
360
则在这个时间段，该中药房的这三种中药的平均销售量为千克.
12. 若甲、乙两人射击比赛的成绩（单位：环）如下：甲：6，7，8，9，10；
乙：7，8，8，8，9.
则甲、乙两人射击成绩比较稳定的是（填甲或乙）；
13. 为庆祝中国共产党建党一百周年，某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分，最终得分按4：3：3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分，则选手甲的最终得分为 分.14. 为了庆祝中国共产党成立100周年，某校举行“党在我心中”演讲比赛，评委将从演讲内容，演讲能力，演讲效果三个方面给选手打分，各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%，演讲效果占10%，计算选手的综合成绩（百分制）.小婷的三项成绩依次是84，95，90，她的综合成绩是.15. 黔东南州某校今年春季开展体操活动，小聪收集、整理了成绩突出的甲、乙两队队员（各50名）的身高得到：平均身高（单位：cm）分别为： ＝160， ，方差分别为： ， ，现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛，根据上述数据，应该选择 .（填写“甲队”或“乙队”）16. 某外贸公司要出口一批规格为 克/盒的红枣，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取 盒进行检测，测得它们的平均质量均为 克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是.（填“甲”或“乙”）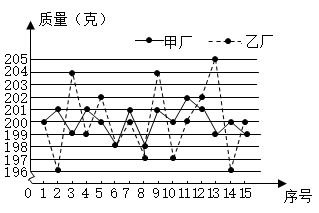
三、解答题
-
17. 农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位： ）进行了测量.根据统计的结果，绘制出如下的统计图①和图②.
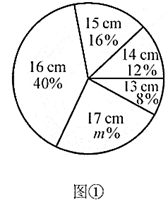
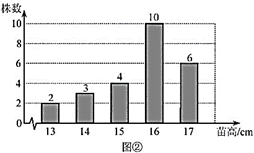
请根据相关信息，解答下列问题：
（Ⅰ）本次抽取的麦苗的株数为 ▲ ，图①中m的值为 ▲ ；
（Ⅱ）求统计的这组苗高数据的平均数、众数和中位数.
18. 某校为了解八年级学生参加社会实践活动情况，随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：
（Ⅰ）本次接受随机抽样调查的学生人数为 ▲ ，图①中的m的值为 ▲ ；
（Ⅱ）求本次抽样调查获取的样本数据的众数、中位数和平均数；
（Ⅲ）若该校八年级学生有240人，估计参加社会实践活动时间大于7天的学生人数．
19. 某学校八、九两个年级各有学生180人，为了解这两个年级学生的体质健康情况，进行了抽样调查，过程如下，请补充完整.收集数据
从八、九两个年级各随机抽取20名学生，进行了体质健康测试，测试成绩（百分制）如下：
八年级
78
86
74
81
75
76
87
70
75
90
75
79
81
70
74
80
86
69
83
77
九年级
93
73
88
81
72
81
94
83
77
83
80
81
70
81
73
78
82
80
70
40
整理、描述数据
按如下分数段整理、描述 这两组样本数据：
成绩
人数x
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
八年级
0
0
1
11
1
九年级
1
0
0
7
（说明：成绩80分及以上为体质健康优秀，70～79分为体质健康良好，60～69分为体质健康合格，60分以下为体质健康不合格）
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示：
年级
平均数
中位数
众数
方差
八年级
78.3
77.5
75
33.6
九年级
78
80.5
52.1
(1)、请将以上两个表格补充完整；(2)、得出结论
估计九年级体质健康优秀的学生人数为；(3)、可以推断出年级学生的体质健康情况更好一些，理由为.（至少从两个不同的角度说明推断的合理性）.20. 近5年，我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例，将这3种家电2016～2020年的产量（单位：万台）绘制成如图所示的折线统计图，图中只标注了甲种家电产量的数据.
观察统计图回答下列问题：
(1)、这5年甲种家电产量的中位数为 万台；(2)、若将这5年家电产量按年份绘制成5个扇形统计图，每个统计图只反映该年这3种家电产量占比，其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°，这个扇形统计图对应的年份是 年；(3)、小明认为：某种家电产量的方差越小，说明该家电发展趋势越好.你同意他的观点吗？请结合图中乙、丙两种家电产量变化情况说明理由.21. 某水果公司以10元/ 的成本价新进2000箱荔枝，每箱质量 ，在出售荔枝前，需要去掉损坏的荔枝，现随机抽取20箱，去掉损坏荔枝后称得每箱的质量（单位： ）如下：4.7··4.8·4.6··4.5··4.8··4.9··4.8··4.7··4.8··4.7
4.8··4.9··4.7··4.8··4.5·4.7··4.7··4.9··4.7··5.0
整理数据：
分析数据：
质量（ ）
4.5
4.6
4.7
4.8
4.9
5.0
平均数
众数
中位数
数量（箱）
2
1
7
3
1
4.75
(1)、直接写出上述表格中 ， ， 的值；(2)、平均数、众数、中位数都能反映这组数据的集中趋势，请根据以上样本数据分析的结果，任意选择其中一个统计量，估算这 箱荔枝共损坏了多少千克？(3)、根据（2）中的结果，求该公司销售这批荔枝每千克定为多少元才不亏本？（结果保留一位小数）22. 某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出5名选手的决赛成绩如图所示.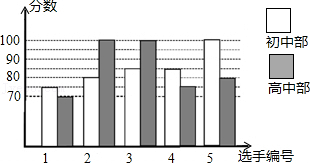
(1)、根据图示填表：平均数（分）
中位数（分）
众数（分）
初中部
85
高中部
85
100
(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.