江苏省无锡市滨湖区、经开区七校2021年数学中考二模联考试卷

试卷更新日期：2021-09-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 5的倒数是（）

A、 $\frac{1}{5}$ B、 $- 5$ C、 $- \frac{1}{5}$ D、 $5$

查看试题解析
2. 函数y＝1＋ $\sqrt{2 - a}$ 中自变量a的取值范围是（）

A、a＞2 B、a≥2 C、a＜2 D、a≤2

查看试题解析
3. 下列运算正确的是（）

A、（－2x²）³＝－6x⁶ B、（y＋x）（－y＋x）＝y²－x² C、2x＋2y＝4xy D、x⁶÷x²＝x⁴

查看试题解析
4. 下列平面图形中，不是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
5. 某中学足球队的18名队员的年龄情况如下表：

年龄（单位：岁）

13

14

15

16

17

人数

3

6

4

4

1

则这些队员年龄的众数和中位数分别是（）

A、14，14 B、14，14.5 C、14，15 D、15，14

查看试题解析
6. 下列说法中，正确的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有一组邻边相等的矩形是正方形 D、对角线互相垂直的四边形是菱形

查看试题解析
7. 已知一次函数 $y = k x + 1$ 的图象经过点A ，且函数值y随x的增大而减小，则点A的坐标可能是 $($ $)$

A、 $(2 ， 4)$ B、 $(- 1 ， 2)$ C、 $(- 1 ， - 4)$ D、 $(5 ， 1)$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，D是边AB上一点，连结CD，将△ACD沿CD翻折得到△ECD，连结BE.若四边形BCDE是平行四边形，则BC的长为（）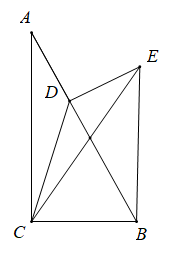

A、 $\sqrt{3}$ B、3 C、2 $\sqrt{3}$ D、3 $\sqrt{2}$

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4，将△ABC绕点A沿顺时针方向旋转后得到△ADE，直线BD、CE相交于点O，连接AO.则下列结论中：①△ABD∽△ACE；②∠COD＝135°；③AO⊥BD；④△AOC面积的最大值为8，其中正确的有（）

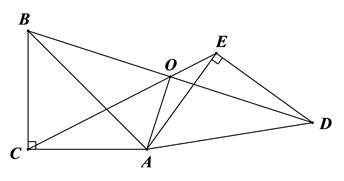A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，已知正方形ABCD的边长为20，点E在弧BD上，∠DEC＝135°，则△DEC的面积为（）

A、20 B、40 C、20 $\sqrt{3}$ D、20 $\sqrt{5}$

查看试题解析

二、填空题

11. 根据滨湖区旅游局数据统计显示，今年“五一”小长假，鼋头渚、灵山圣境、三国水浒城三大5A景区共接待旅游总人数354000人，这个数据用科学记数法可表示为人.

查看试题解析
12. 分解因式：ab²－16a＝.

查看试题解析
13. 用一个圆心角为120°，半径为4的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径为．

查看试题解析
14. 反比例函数y＝ $\frac{k + 1}{x}$ 的图象经过点（－2，3），则k的值为.

查看试题解析
15. 如图，在平面直角坐标系中，点P的坐标为（- $\sqrt{3}$ m，m）（m＞0），过点P的直线AB与x轴负半轴交于点A，与直线y＝－ $\sqrt{3}$ x交于点B.若点A的坐标是（－6，0），且2AP＝3PB，则直线AB的函数表达式为.

查看试题解析
16. 如图，在菱形 $A B C D$ 中， $∠ A B C = 120 ° ， A B = 4$ ，将菱形 $A B C D$ 绕点A逆时针旋转 $30 °$ ，此时点B，C，D的对应点分别为 $B^{'} ， C^{'} ， D^{'}$ ，则图中阴影部分的面积为.

查看试题解析
17. 如图，在矩形ABCD中，E是边BC上一点，连接AE，过点B作BF⊥AE于点G，交直线CD于点F.以BE和BF为邻边作平行四边形BEHF，M是BH的中点，连接GM，若AB＝3，BC＝2，则GM的最小值为.

查看试题解析

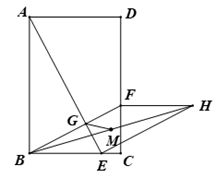
三、解答题

18. 计算：

(1)、4cos30°－ $2^{- 1}$ － $\sqrt{12}$ ；

(2)、 $(a + 2) (a - 2) - {(a - 1)}^{2}$ .

查看试题解析
19. 解下列方程或不等式组：

(1)、 $x^{2} - 6 x + 2 = 0$ ；

(2)、 ${\begin{array}{l} \frac{x + 1}{3} > - 1 \\ - x < 5 x + 12 \end{array}$

查看试题解析
20. 如图，在四边形ABCD中，∠B＝90°，AC平分∠DAB，DE⊥AC，垂足为E，且AE＝AB.

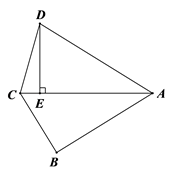(1)、求证：BC＝DE；

(2)、若∠DAC＝40°，求∠CDE的度数.

查看试题解析
21. 某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分别直方图和扇形统计图：

根据图中提供的信息，解答下列问题：

(1)、补全频数分布直方图

(2)、求扇形统计图中m的值和E组对应的圆心角度数

(3)、请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数

查看试题解析
22. 在一个不透明的袋子里装有4个标有－1，－2，3，4的小球，它们的形状、大小完全相同.李强从布袋里随机取出一个小球，记下数字为x，王芳在剩下的3个小球中随机取出一个小球，记下数字为y，这样确定了点M的坐标（x，y）.求点M（x，y）在函数y＝－x＋2的图象上的概率.（用画树状图或列表的方法）

查看试题解析
23. 如图

(1)、如图1，已知线段a，请用无刻度的直尺和圆规作Rt△ABC，使斜边AB＝a，∠A＝30°；

(2)、如图2，已知矩形MNPQ中，MN＝6，若在边PQ上存在一点D，使∠MDN＝30°，则边NP长度的取值范围是.

查看试题解析
24. 如图，已知点E在菱形ABCD的对角线BD上，连接AE，且AE＝BE，⊙O是△ABE的外接圆.

(1)、求证：BC是⊙O的切线；

(2)、若BD＝ $\frac{32 \sqrt{5}}{5}$ ，tan∠OBD＝2，求⊙O的半径.

查看试题解析
25. 为了美化环境，建设宜居成都，我市准备在一个广场上种植甲、乙两种花卉.经市场调查，甲种花卉的种植费用 $y$ （元）与种植面积 $x (m^{2})$ 之间的函数关系如图所示，乙种花卉的种植费用为每平方米100元.

(1)、直接写出当 $0 \leq x \leq 300$ 和 $x > 300$ 时， $y$ 与 $x$ 的函数关系式；

(2)、广场上甲、乙两种花卉的种植面积共 $1200 m^{2}$ ，若甲种花卉的种植面积不少于 $200 m^{2}$ ，且不超过乙种花卉种植面积的2倍，那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少？最少总费用为多少元？

查看试题解析
26. 已知抛物线y=mx²-2mx+3（m<0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB=3OA．

(1)、求抛物线的解析式：

(2)、若M，N是第一象限的抛物线上不同的两点，且ΔBCN的面积恒小于 $△$ BCM的面积，求点M的坐标；

(3)、若D为抛物线的顶点，P为第二象限的抛物线上的一点，连接BP，DP，分别交y轴于E，F，若EF= $\frac{1}{3}$ OC，求点P的坐标．

查看试题解析
27. 如图，△ABC为等边三角形，AB＝6，将边AB绕点A顺时针旋转 $θ$ （0°＜ $θ$ ＜120°）得到线段AD，连接CD，CD与AB交于点G，∠BAD的平分线交CD于点E，F为CD上一点，且DF＝2CF.

(1)、当∠EAB＝30°时，求∠AEC的度数；

(2)、当线段BF的长取最小值时，求线段AG的长；

(3)、请直接写出△ADE的周长的最大值.

查看试题解析

年龄（单位：岁）	13	14	15	16	17
人数	3	6	4	4	1