江苏省常州市金坛区2020-2021学年九年级下学期数学阶段性质量调研（二）

试卷更新日期：2021-09-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列4个实数中，最小的是（）

A、-2 B、 $\frac{1}{2}$ C、0 D、 $\sqrt{2}$

查看试题解析
2. 当 $x = 1$ 时，下列分式没有意义的是（）

A、 $\frac{x + 1}{x}$ B、 $\frac{x}{x - 1}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x + 1}$

查看试题解析
3. 五边形的外角和等于（）

A、180° B、360 ° C、540° D、720°

查看试题解析
4. 如图是一个几何体的侧面展开图，这个几何体是（）

A、长方体 B、圆柱 C、球 D、圆锥

查看试题解析
5. 如图， $A B / / C D$ ， $E F$ 分别与 $A B$ ， $C D$ 交于点 $B$ ， $F$ .若 $∠ E = 30 °$ ， $∠ E F C = 130 °$ ，则 $∠ A$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $30 °$

查看试题解析
6. 对于一次函数 $y = x + 2$ ，下列说法不正确的是（）

A、图象经过点 $(1，3)$ B、图象与x轴交于点 $(- 2，0)$ C、图象不经过第四象限 D、当 $x > 0$ 时， $y < 2$

查看试题解析
7. 如图，线段 AB 经过⊙O 的圆心， AC ， BD 分别与⊙O 相切于点 C ，D ．若 AC =BD = 4 ，∠A=45°，则弧CD的长度为（）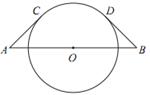

A、π B、2π C、2 $\sqrt{2}$ π D、4π

查看试题解析
8. 如图， $A C$ 、 $B D$ 是菱形 $A B C D$ 的两条对角线，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点A、C且关于直线 $B D$ 对称，若 $A C = 2 \sqrt{2}$ ， $\tan ∠ O A C = 3$ ，则k的值是（）

A、6 B、7 C、8 D、 $6 \sqrt{2}$

查看试题解析

二、填空题

9. 计算： $m^{3} \div m =$ .

查看试题解析
10. 计算： $(\sqrt{5} + 1) (\sqrt{5} - 1)$ =.

查看试题解析
11. 因式分解： $a x^{2} - a y^{2} =$ .

查看试题解析
12. 如果 $a - b + 1 = 0$ ，则 $2 a - 2 b + 1 =$ .

查看试题解析
13. “锐角与钝角是互为补角”是命题.（填写“真”或“假”）

查看试题解析
14. 在平面直角坐标系中，点 $P (2 ， 1)$ 到原点O的距离是.

查看试题解析
15. 若 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是关于x ， y的二元一次方程 $- x + a y = 3$ 的解，则a= ．

查看试题解析
16. 如图， $∠ E B C$ 是 $⊙ O$ 内接四边形 $A B C D$ 的一个外角，若 $∠ C B E = 60 °$ ，则 $∠ A O C =$ $°$ .

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $B D$ 是对角线， $A E ⊥ B D$ ，垂足为E，连接 $C E$ .若 $∠ A D B = 30 °$ ，则如 $\tan ∠ D E C$ 的值为.

查看试题解析
18. 如图，已知菱形 $A B C D$ ， $∠ A B C = 120 °$ ， $B E / / D F$ ， $B E = 4$ ， $D F = 5$ ， $E F = 15$ ， $\sin ∠ B E F = \frac{3}{5}$ ，则 $B C =$ .

查看试题解析

三、解答题

19. 计算：

(1)、 ${(\frac{1}{2})}^{0} + {(\frac{1}{2})}^{- 1} - {(\sqrt{2})}^{2}$ ；

(2)、 $x (x + 2) - (x + 1) (x - 1)$ .

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 x - 2 \leq 1 \\ - 2 x - 1 < 3 \end{array}$ 并把解集在数轴上表示出来.

查看试题解析
21. 如图， $A B = A C$ ， $A D = A E$ ， $B D$ 和 $C E$ 相交于点O.

(1)、求证： $∠ A B D = ∠ A C E$ ；

(2)、判断 $△ B O C$ 的形状，并说明理由.

查看试题解析
22. 2020年3月，中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某区教育局发布了“普通中小学劳动教育状况评价指标”.为了解某校学生一周劳动次数的情况，随机抽取若干学生进行调查，得到如下统计图：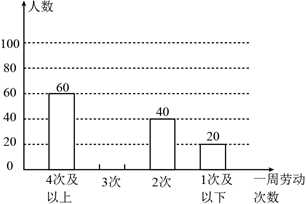

(1)、这次调查活动共抽取人，“2次”所在扇形对应的圆心角是 $°$ ；

(2)、请将条形统计图补充完整；

(3)、若该校学生共有3000人，根据调查结果，请你估计该校一周劳动“4次及以上”的学生人数.

查看试题解析
23. 防疫期间，全区所有学校都严格落实测体温进校园的防控要求.某校开设了A，B，C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.

(1)、小明从A测温通道通过的概率是；

(2)、求小明和小丽从不同的两个测温通道通过的概率.

查看试题解析
24. 第5代移动通信技术简称5G ，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，小明和小强分别用5G与4G下载一部600兆的公益片，小明比小强所用的时间快140秒，求该地4G与5G的下载速度分别是每秒多少兆？

查看试题解析
25. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $A (3 ， a)$ ，点 $B (14 - 2 a ， 2)$ .

(1)、求反比例函数 $y = \frac{m}{x} (x > 0)$ 的表达式；

(2)、若一次函数 $y = k x + b$ 的图象与y轴交于点C，连接 $O B$ ，求 $△ B O C$ 的面积.

查看试题解析
26. 阅读并解答下列问题：在学习完《中心对称图形》一章后，老师给出了以下一个思考题：如图1，在平面直角坐标系 $x O y$ 中，已知点 $A (0 ， 3)$ ， $B (5 ， 1)$ ， $C (a ， 0)$ ， $D (a + 2 ， 0)$ ，连接 $A C$ ， $C D$ ， $D B$ ，求 $A C + C D + D B$ 的最小值.
（思考交流）小明，如图2，先将点A向右平移2个单位长度到点 $A_{1}$ ，作点B关于x轴的对称点 $B_{1}$ ，连接 $A_{1} B_{1}$ 交x轴于点D，将点D向左平移2个单位长度得到点C，连接 $A C$ 、 $B D$ .此时 $A C + C D + D B$ 的最小值等于 $A_{1} B_{1} + C D$ .

小颖：如图3，先将点A向右平移2个单位长度到点 $A_{1}$ ，作点 $A_{1}$ 关于x轴的对称点 $A_{2}$ ，连接 $A_{2} B$ 可以求解.

小亮：对称和平移还可以有不同的组合….

(1)、（尝试解决）在图2中 $A C + C D + D B$ 的最小值是.

(2)、（灵活应用）如图4，在平面直角坐标系 $x O y$ 中，已知点 $A (0 ， 3)$ ， $B (5 ， 1)$ ， $C (a ， 1)$ ， $D (a + 2 ， 0)$ ，连接 $A C$ ， $C D$ ， $D B$ ，则 $A C + C D + D B$ 的最小值是 ▲ ，此时 $a =$ ▲ .并请在图5中用直尺和圆规作出 $A C + C D + D B$ 最小时 $C D$ 的位置（不写作法，保留作图痕迹）.

(3)、（拓展提升）如图6，在平面直角坐标系 $x O y$ 中，已知点 $A (0 ， 3)$ ，C是一次函数 $y = x$ 图象上一点， $C D$ 与y轴垂直且 $C D = 2$ （点D在点C右侧），连接 $A C$ ， $C D$ ， $A D$ ，直接写出 $A C + C D + D A$ 的最小值是，此时点C的坐标是.

查看试题解析
27. 如图，在平面直角坐标系 $x O y$ 中，已知一次函数 $y = \frac{3}{4} x + 6$ 的图象与x轴、y轴分别交于点A、B，点C是线段 $O A$ 的中点，D是线段 $A B$ 上一个动点，连接 $C D$ ，将 $△ A C D$ 沿直线 $C D$ 翻折，使得点A落在点E处，射线 $C E$ 交直线 $A B$ 于点F.

(1)、连接 $B C$ ，求 $B C$ 的长；

(2)、若点F在线段 $A B$ 上，连接 $B E$ ，当 $∠ B E C = 90 °$ 时，求 $A D$ 的长；

(3)、以F为圆心， $F E$ 长为半径作 $⊙ F$ ，若 $⊙ F$ 与x轴相切于点T，求点F的坐标.

查看试题解析
28. 如图，在平面直角坐标系 $x O y$ 中，二次函数 $y = - x^{2} + b x + 3$ 的图象与x轴交于点 $A (- 1 ， 0)$ 和点B（点A在点B的左侧），与y轴交于点C，连接 $A C$ .

(1)、填空： $b =$ ；

(2)、设抛物线的顶点是D，连接 $B C$ ， $B D$ ，将 $∠ A B C$ 绕点B顺时针旋转，当射线 $B C$ 经过点D时，射线 $B A$ 与抛物线交于点P，求点P的坐标；

(3)、设E是x轴上位于点B右侧的一点，F是第一象限内一点， $E F ⊥ x$ 轴且 $E F = 3$ ，点H是线段 $A E$ 上一点，以 $E H$ 、 $E F$ 为邻边作矩形 $E F G H$ ， $F T ⊥ A C$ ，垂足为T，连接 $T G$ ， $T H$ .若 $△ T G F$ 与 $△ T G H$ 相似，求 $O E$ 的长.

查看试题解析