湖北武汉江岸区2021年数学中考模拟试卷
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 下列事件是必然事件的是( )A、路口遇到红灯 B、掷一枚硬币正面朝上 C、三角形的两边之和大于第三边 D、异号两数之和小于零3. 下列交通标识,既是中心对称图形,又是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 4. 计算 的结果正确的是( )A、 B、 C、 D、5. 如图是由6个小正方体搭成的物体,该所示物体的主视图是( )
4. 计算 的结果正确的是( )A、 B、 C、 D、5. 如图是由6个小正方体搭成的物体,该所示物体的主视图是( )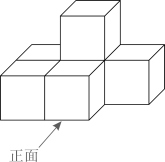 A、
A、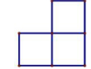 B、
B、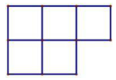 C、
C、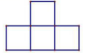 D、
D、 6. 有两把不同的锁和四把钥匙,其中两把钥匙分别能打开这两把锁,其余两把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )A、 B、 C、 D、7. 若点 , , 在反比例函数 (k是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8.
6. 有两把不同的锁和四把钥匙,其中两把钥匙分别能打开这两把锁,其余两把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )A、 B、 C、 D、7. 若点 , , 在反比例函数 (k是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8.在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )
 A、乙先出发的时间为0.5小时 B、甲的速度是80千米/小时 C、甲出发0.5小时后两车相遇 D、甲到B地比乙到A地早 小时9. 有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )
A、乙先出发的时间为0.5小时 B、甲的速度是80千米/小时 C、甲出发0.5小时后两车相遇 D、甲到B地比乙到A地早 小时9. 有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )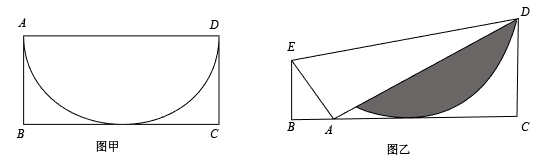 A、 B、 C、 D、10. 如图, , , , 是分别以 , , , 为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点 , , , 均在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、10. 如图, , , , 是分别以 , , , 为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点 , , , 均在反比例函数 的图象上,则 的值为( ) A、 B、6 C、 D、
A、 B、6 C、 D、二、填空题
-
11. 计算 的结果是12. 一组数据 , , , , 的众数是 ,则 =.13. 方程 的解是.14. 如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为58°(A,B,C三点在一条直线上),则建筑物CD的高度为米.(结果保留整数.参考数据: )
 15. 抛物线y=ax2+bx+c(a,b,c是常数,a>0)的对称轴是直线x=1,图象与x轴交于点(-1,0).下列四个结论:
15. 抛物线y=ax2+bx+c(a,b,c是常数,a>0)的对称轴是直线x=1,图象与x轴交于点(-1,0).下列四个结论:①方程ax2+bx+c=0的解为 ;
②3a+c=0;
③对于任意实数t,总有 ;
④不等式 (k为常数)的解集为 或 .
其中正确的结论是(填写序号).
三、解答题
-
16. 实践操作:
第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点 处,得到折痕DE,然后把纸片展平.
第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点 处,点B落在点 处,得到折痕EF, 交AB于点M, F交DE于点N,再把纸片展平.
问题解决:若 ,则 的值为.
 17. 解不等式组 请按以下步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
17. 解不等式组 请按以下步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来; (4)、原不等式组的解集为.18. 如图,D、B分别为AE、FC上的点,∠1=∠2,∠A=∠C.
(4)、原不等式组的解集为.18. 如图,D、B分别为AE、FC上的点,∠1=∠2,∠A=∠C.求证:∠E=∠F.
 19. “生活垃圾分类”逐渐成为社会生活新风尚,我校为了了解学生对“生活垃圾分类”的看法,随机调查了一部分学生(每名学生必须选择且只能选择一类看法),调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:
19. “生活垃圾分类”逐渐成为社会生活新风尚,我校为了了解学生对“生活垃圾分类”的看法,随机调查了一部分学生(每名学生必须选择且只能选择一类看法),调查结果分为“A.很有必要”“B.有必要”“C.无所谓”“D.没有必要”四类.并根据调查结果绘制了图1和图2两幅统计图(均不完整),请根据图中提供的信息,解答下列问题:
 (1)、这次共抽取了名学生进行调查统计,扇形统计图中“D.没有必要”所在扇形的圆心角大小为°;(2)、将条形统计图补充完整;(3)、我校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生约有多少人?20. 如图,点A、B均为格点,线段AB与网络线交于点D.仅用无刻度尺的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示.
(1)、这次共抽取了名学生进行调查统计,扇形统计图中“D.没有必要”所在扇形的圆心角大小为°;(2)、将条形统计图补充完整;(3)、我校共有2500名学生,根据调查结果估计该校对“生活垃圾分类”认为“A.很有必要”的学生约有多少人?20. 如图,点A、B均为格点,线段AB与网络线交于点D.仅用无刻度尺的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示.
( 1 )将线段AB绕点A顺时针旋转90°得线段AC;
( 2 )在AC上找一点E,使∠ABE=∠ACD;
( 3 )在BC上取一点P,使 .
21. 如图,PA、PB与⊙O相切于点A、B,过点B作BD AP交⊙O于点D. (1)、求证:AD=AB;(2)、若 ,求△ABP的面积.22. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.
(1)、求证:AD=AB;(2)、若 ,求△ABP的面积.22. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示. (1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.23. 正方形ABCD中,M为CD中点,N为BC上一点.
(1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.23. 正方形ABCD中,M为CD中点,N为BC上一点. (1)、如图1,若BN=3NC,求证:AM⊥MN;(2)、如图2,在(1)条件下,连结BD交AN,AM于点E、F,若DF=7,求BE的长;(3)、如图3,过点N作NH⊥AN交AM延长线于点H,连接AC交NH于点G,若tan∠BAN= ,则 的值为.(直接写出答案)24. 如图1,抛物线y=x2+bx+c与x轴交于点A、B,OB=3OA=3.
(1)、如图1,若BN=3NC,求证:AM⊥MN;(2)、如图2,在(1)条件下,连结BD交AN,AM于点E、F,若DF=7,求BE的长;(3)、如图3,过点N作NH⊥AN交AM延长线于点H,连接AC交NH于点G,若tan∠BAN= ,则 的值为.(直接写出答案)24. 如图1,抛物线y=x2+bx+c与x轴交于点A、B,OB=3OA=3. (1)、求抛物线解析式;(2)、如图2,直线y=kx+n与抛物线交于点C、D,若△ACD的内心落在x轴上,求k的值;(3)、如图3,直线l与抛物线有且只有一个公共点E,l与抛物线对称轴交于点F,若△AEF的面积为 ,求点E的坐标.
(1)、求抛物线解析式;(2)、如图2,直线y=kx+n与抛物线交于点C、D,若△ACD的内心落在x轴上,求k的值;(3)、如图3,直线l与抛物线有且只有一个公共点E,l与抛物线对称轴交于点F,若△AEF的面积为 ,求点E的坐标.