湖北省武汉市青山区2021年数学中考一模试卷
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 式子 在实数范围内有意义,则x的取值范围是( )A、x<-2 B、x>-2 C、x≥-2 D、x≤-23. 投掷两枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,则下列事件为随机事件的是( )A、两枚骰子向上一面的点数和大于1 B、两枚骰子向上一面的点数和等于1 C、两枚骰子向上一面的点数和等于9 D、两枚骰子向上一面的点数和大于124. 永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标不是轴对称的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,由4个相同的小正方体组成的几何体,则该几何体的俯视图是( )
5. 如图,由4个相同的小正方体组成的几何体,则该几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、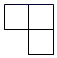 6. 已知点(﹣2,a),(2,b),(3,c)在函数y= (k>0)的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a7. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、8. 如图1,在四边形 中 , ,AC=AD,动点 从点 出发沿折线 的方向以1个单位长度/秒的速度运动.在整个运动的过程中, 的面积 (平方单位与运动时间(秒)的关系如图2所示,则线段AD的长为( )
6. 已知点(﹣2,a),(2,b),(3,c)在函数y= (k>0)的图象上,则下列判断正确的是( )A、a<b<c B、b<a<c C、a<c<b D、c<b<a7. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、8. 如图1,在四边形 中 , ,AC=AD,动点 从点 出发沿折线 的方向以1个单位长度/秒的速度运动.在整个运动的过程中, 的面积 (平方单位与运动时间(秒)的关系如图2所示,则线段AD的长为( )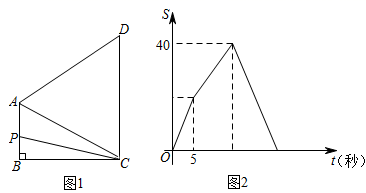 A、 B、8 C、 D、109. 如图, 是半⊙ 的直径,点 是弧 的中点,D为弧BC的中点,连接 , 于点 .则 ( )
A、 B、8 C、 D、109. 如图, 是半⊙ 的直径,点 是弧 的中点,D为弧BC的中点,连接 , 于点 .则 ( ) A、3 B、 C、 D、10. 一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是( )A、9999 B、9910 C、9901 D、9801
A、3 B、 C、 D、10. 一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是( )A、9999 B、9910 C、9901 D、9801二、填空题
-
11. 计算 的结果是 .12. 某市在一次空气污染指数抽查中,收集到6天的数据如下:61,74,70,56,80,91.该组数据的中位数是.13. 计算 的结果是.14. 为 边 上一点,将 沿 翻折得到 ,点 在 上,而且 ,若 ,那么 .
 15. 小明在研究抛物线 ( 为常数)时,得到如下结论:
15. 小明在研究抛物线 ( 为常数)时,得到如下结论:①无论 取何实数, 的值都小于0;
②该抛物线的顶点始终在直线y=-x+1上;
③当 时, 随 的增大而增大,则 ;
④该抛物线上有两点 , ,若 , ,则 .其中一定正确的是(填序号即可).
16. 如图,四边形 中, 与 相交于 点,AE=CE, ,则 .
三、解答题
-
17. 计算: .18. 如图,已知 , .求证
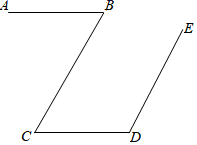 19. 为了解学生网上课堂的学习效果,某中学随机抽取了部分九年级学生进行调查.要求每位学生从“优秀”,“良好”,“不合格”四个等次中,选择一项作为自我评价网课学习的效果,请结合图中所给的信息解答下列问题
19. 为了解学生网上课堂的学习效果,某中学随机抽取了部分九年级学生进行调查.要求每位学生从“优秀”,“良好”,“不合格”四个等次中,选择一项作为自我评价网课学习的效果,请结合图中所给的信息解答下列问题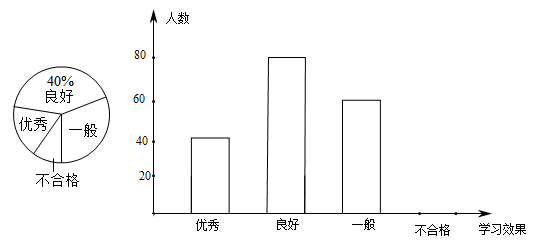 (1)、这次活动共抽查了 ▲ 人,并补全条形统计图;(2)、扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数为.(3)、若该校九年级学生共有500名,根据以上抽样结果,估计该校九年级学生网课学习效果为良好和优秀学生共多少名?20. 如图是由边长为1的小正方形构成的 网格,每个小正方形的顶点叫做格点,四边形 的顶点在格点上,仅用无刻度的直尺按要求作图.(画图过程用虚线表示,画图结果用实线表示)
(1)、这次活动共抽查了 ▲ 人,并补全条形统计图;(2)、扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数为.(3)、若该校九年级学生共有500名,根据以上抽样结果,估计该校九年级学生网课学习效果为良好和优秀学生共多少名?20. 如图是由边长为1的小正方形构成的 网格,每个小正方形的顶点叫做格点,四边形 的顶点在格点上,仅用无刻度的直尺按要求作图.(画图过程用虚线表示,画图结果用实线表示)
( 1 )在 上找一点 ,使 ;
( 2 )在 上找一点 ,连接 ,使 ;
( 3 )在 上找一点 ,连接 ,使 平分四边形 的面积.
21. 如图, 为 的直径,四边形 内接于 ,对角线 , 交于点E, 的切线 交 的延长线于点F,切点为A,且 .
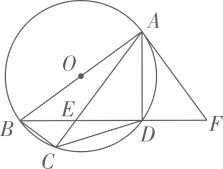 (1)、求证: ;(2)、若 ,求 的值.22. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现销售量y(件)与售价 (元/件)( 为正整数)之间满足一次函数关系:
(1)、求证: ;(2)、若 ,求 的值.22. 一大型商场经营某种品牌商品,该商品的进价为每件3元,根据市场调查发现销售量y(件)与售价 (元/件)( 为正整数)之间满足一次函数关系:(元/件)
4
5
6
(件)
10000
9500
9000
(1)、求 与 的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于15元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润及此时的销售单价分别为多少元?23. 在Rt△ABC中,∠ACB=90°,点D为AB上一点. (1)、如图1,若CD⊥AB,求证:AC2=AD·AB;(2)、如图2,若AC=BC,EF⊥CD交CD于H,交AC于F,且 ,求 的值;(3)、如图3,若AC=BC,点H在CD上,∠AHD=45°,CH=3DH,则tan∠ACH的值为.24. 已知抛物线 与 轴的交点为 、 ,顶点为 .
(1)、如图1,若CD⊥AB,求证:AC2=AD·AB;(2)、如图2,若AC=BC,EF⊥CD交CD于H,交AC于F,且 ,求 的值;(3)、如图3,若AC=BC,点H在CD上,∠AHD=45°,CH=3DH,则tan∠ACH的值为.24. 已知抛物线 与 轴的交点为 、 ,顶点为 . (1)、若点 、点 的坐标分别为 、 ,求抛物线的解析式;(2)、在(1)的条件下,在抛物线的对称轴上是否存在点 使 为直角三角形?若存在;若不存在,请说明理由;(3)、若抛物线 与直线 交于 、 两点,点 在 之间的抛物线上运动, 轴, 是否为定值,并说明理由.
(1)、若点 、点 的坐标分别为 、 ,求抛物线的解析式;(2)、在(1)的条件下,在抛物线的对称轴上是否存在点 使 为直角三角形?若存在;若不存在,请说明理由;(3)、若抛物线 与直线 交于 、 两点,点 在 之间的抛物线上运动, 轴, 是否为定值,并说明理由.