湖北省武汉市江岸区2021年数学中考模拟试卷（三）

试卷更新日期：2021-09-30 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. 实数2021的相反数是（   ）
    A、2021 B、-2021 C、12021 D、−12021

    查看试题解析

  • 2. 下列事件属于必然事件的是（   ）
    A、今天本班全勤 B、太阳从东边升起 C、打了新冠疫苗后就不会感染了 D、掷一枚质地均匀的硬币正面朝上

    查看试题解析

  • 3. 下列智能手机的功能图标中，既是轴对称图形又是中心对称图形的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 计算 (−a2)3 的结果是（ ）
    A、a5 B、−a5 C、a6 D、−a6

    查看试题解析

  • 5. 如图，该几何体是由5个大小相同的正方体组成，它的左视图是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 6. 布袋中装有除颜色外没有其他区别的1个红球和2个白球，搅匀后从中摸出一个球，放回搅匀，再摸出第二个球，两次都摸出白球的概率是（   ）
    A、49 B、29 C、23 D、13  

    查看试题解析

  • 7. 已知 M(x1 ， y1) ， N(x2 ， y2) ， R(x3 ， y3) 是反比例函数 y=k2+1x 图象上三点，若 x1<x2<x3 ， y2<y1<0<y3 ，则下列关系式不正确的是（   ）
    A、x1x2<0 B、x1x3<0 C、x2x3<0 D、x1+x2<0

    查看试题解析

  • 8. 防汛期间，下表记录了某水库16h内水位的变化情况，其中x表示时间（单位：h），y表示水位高度（单位：m），当x＝8h时，达到警戒水位，开始开闸放水，此时，y与x

    x/h

    0

    1

    2

    8

    10

    12

    14

    16

    y/m

    14

    14.5

    15

    18

    14.4

    12

    11

    9

    满足我们学过的某种函数关系.其中开闸放水有一组数据记录错误，它是（   ）

    A、第1小时 B、第10小时 C、第14小时 D、第16小时

    查看试题解析

  • 9. 如图，扇形AOB中，OA＝2，C为 AB⌢ 上的一点，连接AC，BC，如果四边形AOBC为平行四边形，则图中阴影部分的面积为（   ）

    A、2π3−3 B、2π3−23 C、4π3−3 D、4π3−23

    查看试题解析

  • 10. 如图，反比例函数 y=kx(x<0) 交边长为10的等边 △ OAB的两边于C、D两点，OC＝3BD，则k的值（   ）

    A、−93 B、93 C、－ 103 D、103

    查看试题解析

二、填空题

  • 11. 计算 (−3)2 的结果是.

    查看试题解析

  • 12. 某校组织知识大赛，25名参赛同学的得分情况如图所示，这些成绩的中位数是.

    查看试题解析

  • 13. 方程 1x−1=32x−2+1 的解是.

    查看试题解析

  • 14. 如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以12千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时，测得∠NAD＝60°，该飞行器从A处飞行40分钟至B处时，测得∠ABD＝75°，则村庄C、D间的距离为千米.（ 3 ≈1.732，结果保留一位小数）

    查看试题解析

  • 15. 定义[a，b，c]为二次函数y＝ax2＋bx＋c（a≠0）的特征数，下面给出特征数为[2m，1－m，－1－m]的函数的一些结论：①当m≠0时，点(1，0)一定在函数的图象上；②当m＞0时，函数图象截x轴所得的线段长度大于 32 ；③当m＜0时，函数在 x>14 时，y随x的增大而减小；④当m＞0，若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形，则 m=13 ，正确的结论是.（填写序号）

    查看试题解析

  • 16. 如图，在Rt △ ABC中，∠BAC＝90°，AD⊥BC，垂足为点D，线段AE与线段CD相交于点F，且AE＝AB，连接DE，∠E＝∠C，若AD＝3DE，则cosE的值为.

    查看试题解析

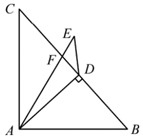
三、解答题

  • 17. 解不等式组 {5x+9>−1①3x−5⩽x+1② 请按下列步骤完成解答：
    (1)、解不等式①，得；
    (2)、解不等式②，得；
    (3)、把不等式①和②的解集在数轴上表示出来；

    (4)、原不等式组的解集为.

    查看试题解析

  • 18. 如图，点A、B、C、D在一条直线上，CE与BF交于点G，∠A＝∠1，∠E＝∠F，求证：CE∥DF.

    查看试题解析

  • 19. 某校积极开展中学生社会实践活动，决定成立文明宣传、环境保护、交通监督三个志愿者队伍，每名学生最多选择一个队伍，为了了解学生的选择意向，随机抽取A，B，C，D四个班，共200名学生进行调查.将调查得到的数据进行整理，绘制成如下统计图（不完整）.

    (1)、求扇形统计图中交通监督所在扇形的圆心角度数；
    (2)、求D班选择环境保护的学生人数，并补全折线统计图；
    (3)、若该校共有学生4000人，试估计该校选择文明宣传的学生人数.

    查看试题解析

  • 20. 在由边长为1的小正方形构成的6×6网格中建立如图所示的平面直角坐标系， △ ABC三个顶点的坐标分别为A(0，3)，B(5，3)，C(1，5).仅用无刻度的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，并回答下列问题：

    (1)、直接写出 △ ABC的形状；
    (2)、作 △ ABC的角平分线CE；
    (3)、在边AB上找一个格点F，连接CF，使∠ACF＝∠AEC，直接写出F点坐标为；
    (4)、根据上述作图，直接写出tan∠AEC的值为.

    查看试题解析

  • 21. 已知，⊙O过矩形ABCD的顶点D，且与AB相切于点E，⊙O分别交BC，CD于H，F，G三点.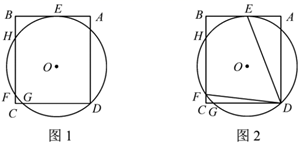

    (1)、如图1，求证：BE－AE＝CG；
    (2)、如图2，连接DF，DE.若AE＝3，AD＝9，tan∠EDF＝ 5 ，求FC的值.

    查看试题解析

  • 22. 某水果经销商以19元/千克的价格新进一批芒果进行销售，因为芒果不耐储存，在运输储存过程损耗率为5%.为了得到日销售量y（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如下表：

    销售价格x（元/千克）

    20

    25

    30

    35

    40

    日销售量y（千克）

    400

    300

    200

    100

    0
    (1)、这批芒果的实际成本为元/千克；[实际成本＝进价÷（1－损耗率）]
    (2)、①请你根据表中的数据直接出写出y与x之间的函数表达式，标出x的取值范围；

    ②该水果经销商应该如何确定这批芒果的销售价格，才能使日销售利润 W1 最大？[日销售利润＝（销售单价－实际成本）×日销售量]

    (3)、该水果经销商参与电商平台助农活动，开展网上直销，可以完全避免运输储存过程中的损耗成本，但每销售1千克芒果需支出a元（a＞0）的相关费用，销售量与销售价格之间关系不变.当25≤x≤29，该水果经销商日获利 W2 的最大值为2156元，求a的值.（日获利＝日销售利润－日支出费用）

    查看试题解析

  • 23. 我们知道：如图1，点C把线段AB分成两部分，如果 BCAC=ACAB ，那么称点C为线段AB的黄金分割点，它们的比值为 5−12 .

    (1)、在图1中，若AB＝6，求AC的长；
    (2)、如图2，用边长为6的正方形纸片进行如下操作：对折正方形ABDE得折痕MN，连接EN，将AE折叠到EN上，点A对应点H，得折痕CE，试说明：C是AB的黄金分割点；
    (3)、如图3，正方形ABCD中，M为对角线BD上一点，点N在边CD上，且CN＜DN，当N为CD的黄金分割点时，∠AMB＝∠ANB，连NM，延长NM交AD于E，则 DEAE 的值为.

    查看试题解析

  • 24. 已知：抛物线y＝a（x＋m）（x－3m）（a＞0，m＞0）与x轴交于A、B两点（点A在点B的右边），与y轴交于点C，直线l：y＝kx＋b经过点B，且与该抛物线有唯一公共点，平移直线l交抛物线于M、N两点（点M、N分别位于x轴下方和上方）

    (1)、若 a=13 ， C(0 ， −1)

    ①直接写出点A，点B的坐标和抛物线的解析式；

    ②如图1，连接AM、AN，取MN的中点P，连接PB，求证：PB⊥AB；

    (2)、如图2，连接MC.若MC∥x轴，求 AMAN 的值.

    查看试题解析