湖北省武汉市洪山区2021年数学中考模拟试卷(5月)
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 式子 在实数范围内有意义,则a的取值范围是( )A、a≥﹣2 B、a≤﹣2 C、a=0 D、a≥23. 下列事件中,是必然事件的是( )
A、任意买一张电影票,座位号是2的倍数 B、13个人中至少有两个人生肖相同 C、车辆随机到达一个路口,遇到红灯 D、明天一定会下雨4. 下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,这是一个由5个完全相同的小正方体组成的立体图形,它的主视图是( )
5. 如图,这是一个由5个完全相同的小正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、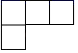 C、
C、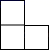 D、
D、 6. 袋中有三个小球,分别为1个红球和2个黄球,它们除颜色外完全相同.随机取出一个小球然后放回,则两次取出的小球颜色不同的概率为( )A、 B、 C、 D、7. 已知A(m+1,y1),B(3﹣m,y2)两点在图象y= +2上,且y1>y2 , 则m的取值范围是( )A、m<1 B、m>3 C、1<m<3 D、﹣1<m<1或m>38. 用描点法画一次函数图象,在如表格中有一组数据错误,这组错误的数据是( )
6. 袋中有三个小球,分别为1个红球和2个黄球,它们除颜色外完全相同.随机取出一个小球然后放回,则两次取出的小球颜色不同的概率为( )A、 B、 C、 D、7. 已知A(m+1,y1),B(3﹣m,y2)两点在图象y= +2上,且y1>y2 , 则m的取值范围是( )A、m<1 B、m>3 C、1<m<3 D、﹣1<m<1或m>38. 用描点法画一次函数图象,在如表格中有一组数据错误,这组错误的数据是( )x
﹣2
﹣1
1
2
y
12
11
10
8
A、(﹣2,12) B、(﹣1,11) C、(1,10) D、(2,8)9. 如图,已知△ABC内接于⊙O,AB=AC,与AC交于点E,连接CD并延长与⊙O过点A的切线交于点F,⊙O的半径为2,则图中阴影部分的面积为( ) A、 ﹣ B、 C、 ﹣ D、1﹣10. 在平面直角坐标系中,反比例函数y= 的图象经过(a,m+2 ),(b,m),则代数式 的值是( )A、 B、﹣ C、2 D、﹣3
A、 ﹣ B、 C、 ﹣ D、1﹣10. 在平面直角坐标系中,反比例函数y= 的图象经过(a,m+2 ),(b,m),则代数式 的值是( )A、 B、﹣ C、2 D、﹣3二、填空题
-
11. =.12. 某车间20名工人日加工零件数如表所示:这些工人日加工零件数的中位数是.
日加工零件数
4
5
6
7
8
人数
2
6
5
4
3
13. 分式方程 的解是.14. 在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,则2号楼的高度为(结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36) 15. 已知抛物线y=ax2+bx+c(a,b,c是常数,且a≠0)与x轴相交于点A,B(点A在点B左侧),其中点A(﹣1,0),C(0,c),其中2≤c≤3,对称轴为直线x=1,①2a+b=0;②当x≥3时,y<0 ;③二次函数的最大值的最小值为4;④﹣1≤a≤﹣ .则其中正确结论的序号为.16. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”,已知正方形ABCD的边长为4dm,则图2中h的值为dm.
15. 已知抛物线y=ax2+bx+c(a,b,c是常数,且a≠0)与x轴相交于点A,B(点A在点B左侧),其中点A(﹣1,0),C(0,c),其中2≤c≤3,对称轴为直线x=1,①2a+b=0;②当x≥3时,y<0 ;③二次函数的最大值的最小值为4;④﹣1≤a≤﹣ .则其中正确结论的序号为.16. 小慧用图1中的一副七巧板拼出如图2所示的“行礼图”,已知正方形ABCD的边长为4dm,则图2中h的值为dm.
三、解答题
-
17. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .18. 如图,AB⊥AD,CD⊥AD,∠1=∠2,求证:DE∥AF
(4)、原不等式组的解集为 .18. 如图,AB⊥AD,CD⊥AD,∠1=∠2,求证:DE∥AF 19. “保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
19. “保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:
 (1)、补全条形统计图;(2)、估计该市这一年(365天)空气质量达到“优”和“良”的总天数;(3)、计算随机选取这一年内的某一天,空气质量是“优”的概率.20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫格点,△ABC的顶点都在格点上(保留作图连线痕迹),并回答问题.
(1)、补全条形统计图;(2)、估计该市这一年(365天)空气质量达到“优”和“良”的总天数;(3)、计算随机选取这一年内的某一天,空气质量是“优”的概率.20. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫格点,△ABC的顶点都在格点上(保留作图连线痕迹),并回答问题.
( 1 )在BC的右边找格点D,连AD,使AD平分∠BAC.
( 2 )若AD与BC交于E,直接写出 的值.
( 3 )找格点F,连EF,使EF⊥AB于H.
( 4 )在AC上找点G,连EG,使EG∥AB.
21. 如图,AB是⊙O的直径,AC交⊙O于点D,点E时弧AD的中点,BE交AC于点F,BC=FC. (1)、求证:BC是⊙O的切线;(2)、若BF=3EF,求tan∠ACE的值.22. 某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类;B类杨梅深加工后再销售,A类杨梅的包装成本为1万元/吨,根据市场调查,平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨,
(1)、求证:BC是⊙O的切线;(2)、若BF=3EF,求tan∠ACE的值.22. 某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类;B类杨梅深加工后再销售,A类杨梅的包装成本为1万元/吨,根据市场调查,平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨,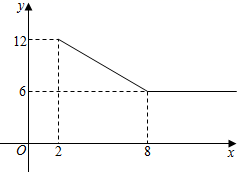 (1)、直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)、第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的总利润为w万元,求w关于x的函数关系式;(3)、第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大利润,并求出最大利润.23. 在 中,∠BAC=90°,AB=AC,D为BC的中点,F,E是AC上两点,连接BE、DF交于 内的一点G,且∠EGF=45°.
(1)、直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)、第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的总利润为w万元,求w关于x的函数关系式;(3)、第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大利润,并求出最大利润.23. 在 中,∠BAC=90°,AB=AC,D为BC的中点,F,E是AC上两点,连接BE、DF交于 内的一点G,且∠EGF=45°. (1)、如图1,若AE=3CE=3,求BG的长;(2)、如图2,若E为AC上任意一点,连接AG,求 ;(3)、若E为AC的中点,求EF:FD的值.24. 已知抛物线y=ax2+bx﹣3经过A(﹣1,0),且与x轴右侧交于B点,对称轴为直线x=1,与y轴交于C点.
(1)、如图1,若AE=3CE=3,求BG的长;(2)、如图2,若E为AC上任意一点,连接AG,求 ;(3)、若E为AC的中点,求EF:FD的值.24. 已知抛物线y=ax2+bx﹣3经过A(﹣1,0),且与x轴右侧交于B点,对称轴为直线x=1,与y轴交于C点. (1)、求抛物线的解析式;(2)、如图1,过点C作直线l∥x轴交抛物线于点D,点P在抛物线上,且∠DCP=∠ACO,求点P的坐标;(3)、如图2,直线y=kx+b(k≠b)交抛物线于M、N两点,NH⊥x轴于点H,HQ与MN相交于点Q,求点Q的横坐标.
(1)、求抛物线的解析式;(2)、如图1,过点C作直线l∥x轴交抛物线于点D,点P在抛物线上,且∠DCP=∠ACO,求点P的坐标;(3)、如图2,直线y=kx+b(k≠b)交抛物线于M、N两点,NH⊥x轴于点H,HQ与MN相交于点Q,求点Q的横坐标.