湖北省黄石市2021年数学中考模拟试卷(6月)
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. 下列算式中,运算结果为负数的是( )A、 B、 C、 D、2. 下列图形中,是中心对称但不是轴对称的图形是( )A、
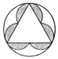 B、
B、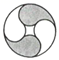 C、
C、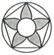 D、
D、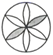 3.
3.如图,你能看出这个倒立的水杯的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、2x+3y=5xy B、(a﹣b)2=a2﹣b2 C、5m2•m3=5m5 D、m2•m3=m65. 函数y= 中自变量x的取值范围是( )A、 且 B、 C、 D、6. 一组数据由4个数组成,其中3个数分别为2,3,4,且这组数据的平均数为4,则这组数据的中位数为( )A、7 B、4 C、3.5 D、37. 如图,在平面直角坐标系xOy中,点A的坐标为(2,1),如果将线段OA绕点O逆时针方向旋转90°,那么点A的对应点的坐标为( )
4. 下列运算正确的是( )A、2x+3y=5xy B、(a﹣b)2=a2﹣b2 C、5m2•m3=5m5 D、m2•m3=m65. 函数y= 中自变量x的取值范围是( )A、 且 B、 C、 D、6. 一组数据由4个数组成,其中3个数分别为2,3,4,且这组数据的平均数为4,则这组数据的中位数为( )A、7 B、4 C、3.5 D、37. 如图,在平面直角坐标系xOy中,点A的坐标为(2,1),如果将线段OA绕点O逆时针方向旋转90°,那么点A的对应点的坐标为( )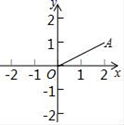 A、(﹣1,2) B、(﹣2,1) C、(1,﹣2) D、(2,﹣1)8. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A、(﹣1,2) B、(﹣2,1) C、(1,﹣2) D、(2,﹣1)8. 如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )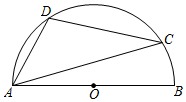 A、10° B、14° C、16° D、26°9. 如图,在△ABC中,∠C=90°,以点B为圆心,以适当长为半径画弧交AB,BC于P、Q两点,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线BN交AC于点D.若AB=10,AC=8,则CD的长是( )
A、10° B、14° C、16° D、26°9. 如图,在△ABC中,∠C=90°,以点B为圆心,以适当长为半径画弧交AB,BC于P、Q两点,再分别以点P,Q为圆心,大于 PQ的长为半径画弧,两弧相交于点N,射线BN交AC于点D.若AB=10,AC=8,则CD的长是( )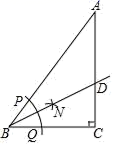 A、2 B、2.4 C、3 D、410. 抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过A(2,0),B(-4,0)两点,下列四个结论:
A、2 B、2.4 C、3 D、410. 抛物线y=ax2+bx+c(a,b,c为常数,a<0)经过A(2,0),B(-4,0)两点,下列四个结论:①一元二次方程ax2+bx+c=0的根为 ②若点 在该抛物线上,则 ③对于任意实数t,总有 ;④对于a的每一个确定值,若一元二次方程ax2+bx+c=p(p为常数,p>0)的根为整数,则p的值只有两个,其中正确的序号是( )
A、①③ B、①②③ C、②③ D、①②④二、填空题
-
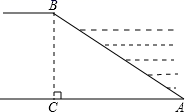
11. 计算: .12. 把多项式 分解因式的结果是 .13. 随着交通网络的不断完善,旅游业持续升温.据统计,在今年“两节”期间,我市某风景区接待游客403000人,这个数据用科学记数法表示为.14. 不等式 的最大整数解是 .15. 河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡度是 ,(坡度是坡面的铅垂高度BC与水平宽度AC之比),则AB的长是.
 16. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是
16. 如图,一个正比例函数图象与一次函数y=-x+1的图象相交于点P,则这个正比例函数的表达式是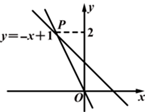 17. 如图,在平面直角坐标系中,函数 与 的图象交于点 ,则代数式 的值为
17. 如图,在平面直角坐标系中,函数 与 的图象交于点 ,则代数式 的值为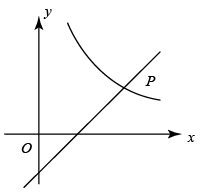 18. 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论:①AE=BF;②AE⊥BF;③ ;④ .正确序号是.
18. 如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论:①AE=BF;②AE⊥BF;③ ;④ .正确序号是.
三、解答题
-
19. 化简并求值: ,其中 .20. 如图,AC是四边形ABCD的对角线,∠1=∠B,点E、F分别在AB、BC上,BE=CD,BF=CA,连接EF.
 (1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.21. 已知:关于x的方程(1)、求证:无论k为何实数,方程总有实数根;(2)、若此方程有两个实数根x1 , x2 , 且|x1﹣x2|=2,求k的值.22. 为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :家庭汽车, :公交车, :电动车, :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)、求证:∠D=∠2;(2)、若EF∥AC,∠D=78°,求∠BAC的度数.21. 已知:关于x的方程(1)、求证:无论k为何实数,方程总有实数根;(2)、若此方程有两个实数根x1 , x2 , 且|x1﹣x2|=2,求k的值.22. 为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :家庭汽车, :公交车, :电动车, :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.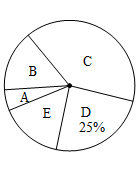
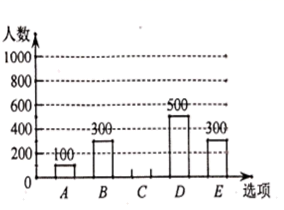 (1)、本次调查中,一共调查了名市民;扇形统计图中, 项对应的扇形圆心角是 ;(2)、补全条形统计图;(3)、若甲上班时从 三种交通工具中随机选择一种, 乙上班时从 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选 种交通工具上班的概率.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买获得第十届矛盾文学奖的《北上》(徐则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需100元;购买6本《北上》与购买7本《牵风记》的价格相同.(1)、求这两种书的单价;(2)、若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E , 交AC于点F , 过点C作CG⊥AB交AB于点G , 交AE于点H , 过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP , BP恰好为⊙O的切线.
(1)、本次调查中,一共调查了名市民;扇形统计图中, 项对应的扇形圆心角是 ;(2)、补全条形统计图;(3)、若甲上班时从 三种交通工具中随机选择一种, 乙上班时从 三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选 种交通工具上班的概率.23. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买获得第十届矛盾文学奖的《北上》(徐则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需100元;购买6本《北上》与购买7本《牵风记》的价格相同.(1)、求这两种书的单价;(2)、若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?24. 如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E , 交AC于点F , 过点C作CG⊥AB交AB于点G , 交AE于点H , 过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP , BP恰好为⊙O的切线.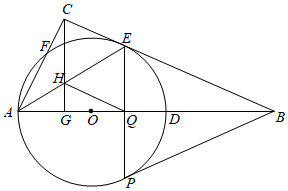 (1)、求证:BC是⊙O的切线.(2)、求证: = .(3)、若sin∠ABC═ ,AC=15,求四边形CHQE的面积.25. 已知:在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A在x轴负半轴上,点B在x轴正半轴上,且CO=BO=3AO,AB=4,抛物线的顶点为D.(1)、求这个二次函数的解析式;(2)、若过点B的直线垂直于BD且与直线CD交于点P,求点P的坐标.(3)、点E(0,n)在y轴正半轴上,且位于点C的下方.当n在什么范围内取值时∠CBD<∠CED?当n在什么范围内取值时∠CBD>∠CED?
(1)、求证:BC是⊙O的切线.(2)、求证: = .(3)、若sin∠ABC═ ,AC=15,求四边形CHQE的面积.25. 已知:在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A在x轴负半轴上,点B在x轴正半轴上,且CO=BO=3AO,AB=4,抛物线的顶点为D.(1)、求这个二次函数的解析式;(2)、若过点B的直线垂直于BD且与直线CD交于点P,求点P的坐标.(3)、点E(0,n)在y轴正半轴上,且位于点C的下方.当n在什么范围内取值时∠CBD<∠CED?当n在什么范围内取值时∠CBD>∠CED?