河南省周口市沈丘县2021年数学中考二模试卷
试卷更新日期:2021-09-30 类型:中考模拟
一、单选题
-
1. 下列各数,绝对值比1小的数是( )A、-3 B、-1 C、0 D、22. 下列几何体中,其主视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、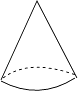 3. 2021年2月20日,党史学习教育动员大会在北京召开.习近平总书记号召全党同志要以优异成绩迎接建党一百周年.中央组织部党内统计数据显示,截至2019年底,中国共产党党员总数为9191.4万名,约为9191万.将9191万用科学记数法表示为( )A、 B、 C、 D、4. 如果 , ,那么一次函数 的图象大致是( )A、
3. 2021年2月20日,党史学习教育动员大会在北京召开.习近平总书记号召全党同志要以优异成绩迎接建党一百周年.中央组织部党内统计数据显示,截至2019年底,中国共产党党员总数为9191.4万名,约为9191万.将9191万用科学记数法表示为( )A、 B、 C、 D、4. 如果 , ,那么一次函数 的图象大致是( )A、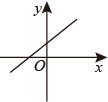 B、
B、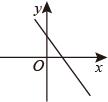 C、
C、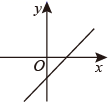 D、
D、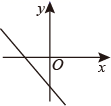 5. 如图, , , , , 相互外离,它们的半径都是2,顺次连接五个圆心得到五边形 ,则图中五个扇形(阴影部分)的面积之和是( )
5. 如图, , , , , 相互外离,它们的半径都是2,顺次连接五个圆心得到五边形 ,则图中五个扇形(阴影部分)的面积之和是( ) A、 B、 C、 D、6. 为实数, ,那么 的值为( )A、1 B、-4或1 C、-4 D、4或-17. 已知函数 ,其中 表示 时的函数值,则 的值为( )A、2020 B、2021 C、4040 D、40418. 在 的正方形方格中, 和 的位置和大小分别如图所示,则 ( )
A、 B、 C、 D、6. 为实数, ,那么 的值为( )A、1 B、-4或1 C、-4 D、4或-17. 已知函数 ,其中 表示 时的函数值,则 的值为( )A、2020 B、2021 C、4040 D、40418. 在 的正方形方格中, 和 的位置和大小分别如图所示,则 ( )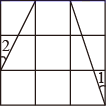 A、30° B、45° C、60° D、75°9. 如图, 和 都是边长为2 cm的等边三角形,它们的边 , 在同一条直线 上,点 , 重合,现将 沿着直线 以2cm/s的速度向右移动, 沿着直线 以1cm/s的速度向右移动,直至点 与 重合时停止移动.在此过程中,设点 移动的时间为 ,两个三角形重登部分的面积为 ,则 随 变化的函数图象大致为( )
A、30° B、45° C、60° D、75°9. 如图, 和 都是边长为2 cm的等边三角形,它们的边 , 在同一条直线 上,点 , 重合,现将 沿着直线 以2cm/s的速度向右移动, 沿着直线 以1cm/s的速度向右移动,直至点 与 重合时停止移动.在此过程中,设点 移动的时间为 ,两个三角形重登部分的面积为 ,则 随 变化的函数图象大致为( ) A、
A、 B、
B、 C、
C、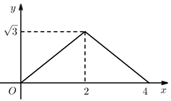 D、
D、 10. 引理:在 中,若 为 的中点,则 .(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形 中, , ,点 在以 为直径的半圆上运动,则 的最小值是( )
10. 引理:在 中,若 为 的中点,则 .(中线长公式,不用证明,可以直接应用)根据这个引理,解决下面的问题:如图,在矩形 中, , ,点 在以 为直径的半圆上运动,则 的最小值是( ) A、 B、38 C、40 D、68
A、 B、38 C、40 D、68二、填空题
-
11. 不透明袋子中装有9个球,其中有2个红球、3个绿球和4个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是蓝球的概率是.12. 《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?”如果设木条长x尺,绳子长y尺,可列方程组为;13. 解方程: , .14. 如图,在梯形 中, 是边 的中点,对角线 平分 ,连接 ,交 于点 ,其中 , ,则 的长为.
 15. 如图,在 中, , , 为边 的中点,若 ,则 的长度为.
15. 如图,在 中, , , 为边 的中点,若 ,则 的长度为.
三、解答题
-
16. 已知 , ,且 ,求 的值.17. 为支持新冠肺炎疫情防控工作,响应中央号召,全国广大人民踊跃捐款.某校七年级全体同学参加了“我为抗疫出份力”的捐款活动,随机抽查了部分同学捐款的情况,统计如图所示,
 (1)、本次抽查的学生人数是多少?补全条形统计图.(2)、本次捐款金额的众数和中位数分别是多少元?(3)、以全校七年级学生按800名估计,捐款总金额约有多少元?18. 2017年9月,中俄海军在日本海进行“海上联合–2017”军事演习.反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1300米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ≈1.7)
(1)、本次抽查的学生人数是多少?补全条形统计图.(2)、本次捐款金额的众数和中位数分别是多少元?(3)、以全校七年级学生按800名估计,捐款总金额约有多少元?18. 2017年9月,中俄海军在日本海进行“海上联合–2017”军事演习.反潜演习中,我军舰A测得潜艇C的俯角为30°.位于军舰A正上方1300米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离海平面的下潜深度.(结果保留整数.参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ≈1.7) 19. 冰封文教店用1200元购进了甲、乙两种钢笔,已知甲种钢笔进价为每支12元,乙种钢笔进价为每支10元。在销售时甲种钢笔售价为每支15元,乙种钢笔售价为每支12元,全部售完后共获利270元。
19. 冰封文教店用1200元购进了甲、乙两种钢笔,已知甲种钢笔进价为每支12元,乙种钢笔进价为每支10元。在销售时甲种钢笔售价为每支15元,乙种钢笔售价为每支12元,全部售完后共获利270元。
(1)、求冰封文教店购进甲、乙两种钢笔各多少支?(2)、冰封文教店以原价再次购进甲、乙两种钢笔,且购进甲种钢笔的数量不变,而购进乙种钢笔的数量是第一次的2倍,乙种钢笔按原售价销售,而甲种钢笔降价销售,当两种钢笔销售完毕时,要使再次购进的钢笔获利不少于340元,甲种钢笔每支最低售价应为多少元?
20. 如图, 是 的切线, 是直径, 是弦,连接 ,且 . (1)、求证: 是 的切线;(2)、若 ,连接 , 的平分线交 于点 ,求 的值.21. 如图,在平面直角坐标系中,点 在反比例函数 的图象上,点 在反比例函数 的图象上,矩形 与坐标轴的交点分别为 , , , , 轴,连接 , ,分别交坐标轴于点 , ,连接 .
(1)、求证: 是 的切线;(2)、若 ,连接 , 的平分线交 于点 ,求 的值.21. 如图,在平面直角坐标系中,点 在反比例函数 的图象上,点 在反比例函数 的图象上,矩形 与坐标轴的交点分别为 , , , , 轴,连接 , ,分别交坐标轴于点 , ,连接 . (1)、求证: 为定值;(2)、若 为 的中点,求 .22. 如图,已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,且 .
(1)、求证: 为定值;(2)、若 为 的中点,求 .22. 如图,已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,且 . (1)、求抛物线的解析式:(2)、如图,证明:对于 轴上任意一点 ,都存在过点 的直线交抛物线于 , 两点,使得 ;(3)、将该抛物线在 之间的部分图象记为 ,将图象 在直线 下方的部分沿 翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为 ,最小值为 ,若 ,求 的取值范围.23. 问题情景:如图1,我们把对角线互相垂直的四边形叫做“垂美四边形”,按照此定义,我们学过的平行四边形中的菱形、正方形等都是“垂美四边形”,“菱形”也是“垂美四边形”.
(1)、求抛物线的解析式:(2)、如图,证明:对于 轴上任意一点 ,都存在过点 的直线交抛物线于 , 两点,使得 ;(3)、将该抛物线在 之间的部分图象记为 ,将图象 在直线 下方的部分沿 翻折,其余部分保持不变,得到一个新的函数的图象,记这个函数的最大值为 ,最小值为 ,若 ,求 的取值范围.23. 问题情景:如图1,我们把对角线互相垂直的四边形叫做“垂美四边形”,按照此定义,我们学过的平行四边形中的菱形、正方形等都是“垂美四边形”,“菱形”也是“垂美四边形”.

概念理解:
(1)、如图2,已知等腰梯形 是“垂美四边形”, , ,求 的长.(2)、如图3,已知四边形 是“垂美四边形”,试探究其两组对边 , 与 , 之间的数量关系,并写出证明过程.(3)、如图4,分别以 的直角边 和斜边 为边向外作正方形 与正方形 ,连接 , , , 与 交于点 ,已知 , ,求 的中线 的长.