福建省南平市2021年数学初中毕业班综合练习（二）

试卷更新日期：2021-09-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数3的算术平方根是（）

A、-3 B、3 C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 中新网北京2021年4月2日电，截至4月2日15时，北京累计接种新冠疫苗人数累计接种新冠疫苗超16 000 000剂次.数据16 000 000可用科学记数法表示为（）

A、16×10⁶ B、1.6×10⁷ C、0.16×10⁸ D、1.6×10⁶

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ C、 $\sqrt{8} - \sqrt{2} = 2$ D、 $\sqrt{8} - \sqrt{2} = 2 \sqrt{2}$

查看试题解析
4. 下列的图形中，不属于中心对称的是（）

A、平行四边形 B、等边三角形 C、正方形 D、圆

查看试题解析
5. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4.若一次摸出1个，则取出的小球标号小于4的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
6. 估计 $\sqrt{3} + 1$ 的值在（）

A、－1到0之间 B、0到l之间 C、1到2之间 D、2到3之间

查看试题解析
7. 如图，点A，B，C在小正方形的顶点上，且每个小正方形的边长为1，则sin∠BAC的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 某班有50名学生，某日晨检测体温统计如下表：

体温/℃

36.2

36.3

36.4

36.5

36.6

36.7

人数

9

10

12

11

7

1

根据上表的信息，下面关于体温的判断正确的选项有（）个

①中位数36.4℃ ②平均数36.4℃ ③众数36.4℃

A、1 B、2 C、3 D、0

查看试题解析
9. 已知点 $A ， B ， C$ 在 $⊙ O$ 上．则下列命题为真命题的是（）

A、若半径 $O B$ 平分弦 $A C$ ．则四边形 $O A B C$ 是平行四边形 B、若四边形 $O A B C$ 是平行四边形．则 $∠ A B C = 120 °$ C、若 $∠ A B C = 120 °$ ．则弦 $A C$ 平分半径 $O B$ D、若弦 $A C$ 平分半径 $O B$ ．则半径 $O B$ 平分弦 $A C$

查看试题解析
10. 如图，平面直角坐标系中，△ABC的边AC=BC= $\frac{5}{2}$ ，AB=4 ，且AB⊥x轴于点A，反比例函数 $y = k x (x > 0)$ 的图象经过点C，交AB于点D，当BD=BC时，则k的值等于（）

A、2 B、3 C、6 D、9

查看试题解析

二、填空题

11. 计算：﹣1+3= ．

查看试题解析
12. 因式分解： $a^{3} - 4 a =$ ．

查看试题解析
13. 用一个圆心角为 $90^{°}$ ，半径为 $20 cm$ 的扇形纸片围成一个圆锥的侧面，这个圆锥的底面圆半径为 $cm$ .

查看试题解析
14. 《孙子算经》上有一著名问题就是“物不知数问题”.原文是这么说的：“有物不知其数，三三数之余二，五五数之余三，七七数之余二.问物几何？”把这个问题翻译为：一个数被3除余2，被5除余3，被7除余2，求这个数？请你写出符合条件的一个数是 .

查看试题解析
15. 如图，点D是等边△ABC内一点，将△BDC以点C为中心顺时针旋转60°，得到△ACE，连接BE，若∠AEB＝45°，则∠DBE的度数为.

查看试题解析
16. 如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A₁B₁C₁ ，点P、Q分别是AB、A₁C₁的中点，PQ的最小值等于.

查看试题解析

三、解答题

17. 计算：(π－2021)⁰+2^-2－ $\sqrt{12}$ + $\sqrt{27}$ .

查看试题解析
18. 解不等式组： ${\begin{array}{l} 2 (x - 2) \leq 2 - x \\ \frac{x + 2}{2} > \frac{x + 3}{3} \end{array}$

查看试题解析
19. 如图，平行四边形ABCD中E，F是直线AC上两点，且AE＝CF.求证：BE∥DF.

查看试题解析
20. 先化简再求值： $(m - 1 - \frac{8}{m + 1}) \div \frac{m^{2} - 6 m + 9}{m + 1}$ ，其中 $m = \frac{2}{3}$ .

查看试题解析
21. 如图，在△ABC中，∠BAC＞∠ACB.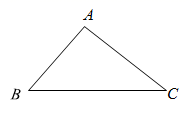

(1)、在BC边上找一点D，使得AB²=BD·BC (要求：用尺规作图，保留作图痕迹，不写作法和证明)

(2)、在（1）的条件下，若AB=4，AC=5， BD：DC=1：3，求AD的长.

查看试题解析
22. “校园手机”现象越来越受到社会的关注.“五一”期间，小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的两个不完整的统计图：
根据以上信息，解答下列问题：

(1)、求这次调查的家长人数，并补全图①；

(2)、求图②中表示家长“赞成”的圆心角的度数；

(3)、从这次接受调查的学生中，随机抽查一个，恰好是“无所谓”态度的学生的概率是多少？请你对学生使用手机提一条建议.

查看试题解析
23. 如图，在直角坐标系xOy中，直线y=2x+6 与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于点A(1，m)，与x轴交于点B ，与y 轴交于点D .

(1)、求m的值和反比例函数的表达式；

(2)、在y轴上有一动点P（0，n），过点P作平行于x轴的直线，交反比例函数的图象于点M，交直线AB于点N，且点M在点A下方，连接BM.若 $S_{Δ B N M} = \frac{1}{4} S_{Δ B O D}$ ，求n的值.

查看试题解析
24. 如图1，在直角△ABC中，∠ACB=90°，AO是△ABC的角平分线，以O为圆心，OC为半径作圆O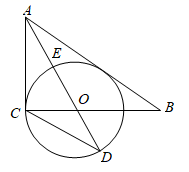

(1)、求证：AB是⊙O的切线；

(2)、已知AO交圆O于点E，延长AO交圆O于点D，tan∠D= $\frac{1}{2}$ ，求 $\frac{A E}{A C}$ 的值；

(3)、如图2，在（2）条件下，若AB与⊙O的切点为点F，连接CF交AD于点G，设⊙O的半径为3，求CF的长.

查看试题解析
25. 在平面直角坐标系中，O为原点，A为x轴正半轴上的动点，经过点A（t，0）作垂直于x轴的直线l，在直线l上取点B，点B在第一象限，AB=4，直线OB：y₁=kx（k为常数）.

(1)、当t=2时，求k的值；

(2)、经过O，A两点作抛物线y₂=ax（x﹣t）（a为常数，a＞0），直线OB与抛物线的另一个交点为C.
①用含a，t的式子表示点C的横坐标；

②当t≤x≤t+4时，|y₁﹣y₂|的值随x的增大而减小；当x≥t+4时，|y₁﹣y₂|的值随x的增大而增大，求a与t的关系式并直接写出t的取值范围.

查看试题解析

体温/℃	36.2	36.3	36.4	36.5	36.6	36.7
人数	9	10	12	11	7	1